Liczby rzeczywiste
Zadania z matur CKE dla liceum ogólnokształcącego - poziom podstawowy
dodawanie, odejmowanie, mnożenie, dzielenie, potęgowanie, pierwiastkowanie, logarytmowanie w zbiorze liczb rzeczywistych
własności pierwiastków dowolnego stopnia, w tym pierwiastków stopnia nieparzystego z liczb ujemnych
związek pierwiastkowania z potęgowaniem oraz prawa działań na potęgach i pierwiastkach
własności monotoniczności potęgowania, w szczególności własności: jeśli x\lessdot y
i a>1 , to a^x\lessdot a^y , zaś jeśli x\lessdot y
i a\in(0,1) , to a^x> a^y
przedział liczbowy, przedziały na osi liczbowej
interpretacja geometryczna i algebraiczna wartości bezwzględnej, równania i nierówności typu |x+4|=5 ,
|x-2|\lessdot 3 , |x+3|\geqslant 4
własności potęgowania i pierwiastkowania w sytuacjach praktycznych, w tym do obliczania procentów
składanych, zysków z lokat i kosztów kredytów
związek logarytmowania z potęgowaniem, logarytm iloczynu, logarytm ilorazu i logarytm potęgi
Zadania obowiązujące do kartkówki po dziale II:
Zadania należy rozwiązać do dnia 30 listopada 2025 r. Część z tych zadań będzie
rozwiązywana na lekcjach w poniedziałek 24.11 i we wtorek 25.11.2025 r.
2,3,5,7,9,10,11,12,13,16,18,19,20,21,23,24,26,27,29,32,33,34,35,37,38,40,41,44,46,47,48,50,52,
53,54,57,59,61,62,63,65,67,71,73,74,75,76,77,79,80,82,83,84,85,86
Minimum wymagane do poprawy kartkówki:
z oceny niedostatecznej: 56,9%
z innej oceny: 50,6%
Zadanie 1. (1 pkt) (Numer zadania: pp-11757)
[ ⇒ Rozwiąż ]
Podpunkt 1.1 (0.2 pkt)
Zbiór
A=(-\infty, 3\rangle\cup\langle 10,+\infty)
jest rozwiązaniem nierówności
|x-a|\ ...\ b .
Wskaż brakujący znak nierówności:
Odpowiedzi:
A. >
B. \geqslant
C. \lessdot
D. \leqslant
Podpunkt 1.2 (0.8 pkt)
Odpowiedzi:
Zadanie 2. (1 pkt) (Numer zadania: pp-11758)
[ ⇒ Rozwiąż ]
Podpunkt 2.1 (1 pkt)
Liczba
\sqrt[3]{-\frac{343}{32}}\cdot\sqrt[3]{4} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 3. (1 pkt) (Numer zadania: pp-11759)
[ ⇒ Rozwiąż ]
Podpunkt 3.1 (1 pkt)
Liczba
\log_{4}{8}+\log_{4}{2}
jest równa:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Zadanie 4. (1 pkt) (Numer zadania: pp-11778)
[ ⇒ Rozwiąż ]
Podpunkt 4.1 (1 pkt)
Wszystkich liczb całkowitych dodatnich spełniających nierówność
|x+3|\lessdot 31 jest:
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
Zadanie 5. (1 pkt) (Numer zadania: pp-11779)
[ ⇒ Rozwiąż ]
Podpunkt 5.1 (1 pkt)
Dla każdej dodatniej liczby rzeczywistej
x iloczyn
\sqrt{x}\cdot \sqrt[3]{x}\cdot \sqrt[7]{x} jest równy
\sqrt[a]{x^b} .
Podaj liczbę \frac{a}{b} .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 6. (1 pkt) (Numer zadania: pp-11780)
[ ⇒ Rozwiąż ]
Podpunkt 6.1 (1 pkt)
Klient wpłacił do banku
10000 zł na lokatę dwuletnią. Po każdym rocznym okresie
oszczędzania bank dolicza odsetki w wysokości
11\% od kwoty bieżącego kapitału
znajdującego się na lokacie.
Po dwóch latach oszczędzania łączna wartość doliczonych odsetek na tej lokacie (bez
uwzględniania podatków) jest równa
S zł.
Podaj liczbę S .
Odpowiedź:
S\ [zl]=
(liczba zapisana dziesiętnie)
Zadanie 7. (1 pkt) (Numer zadania: pp-11781)
[ ⇒ Rozwiąż ]
Podpunkt 7.1 (1 pkt)
Liczba
\log_{2}{\frac{1}{16}}+\log_{2}{8}
jest równa:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Zadanie 8. (1 pkt) (Numer zadania: pp-11804)
[ ⇒ Rozwiąż ]
Podpunkt 8.1 (1 pkt)
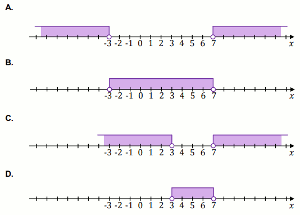
Dana jest nierówność
|x-5|\lessdot 2 oraz zbiory zaznaczone na osi liczbowej:
Rozwiązanie tej nierówności pokazano na rysunku:
Odpowiedzi:
Zadanie 9. (1 pkt) (Numer zadania: pp-11803)
[ ⇒ Rozwiąż ]
Podpunkt 9.1 (1 pkt)
Liczba
3\sqrt{12}-\sqrt{147} jest równa:
Odpowiedź:
Wpisz odpowiedź:
\cdot √
(wpisz dwie liczby całkowite)
Zadanie 10. (1 pkt) (Numer zadania: pp-11805)
[ ⇒ Rozwiąż ]
Podpunkt 10.1 (1 pkt)
Liczba
\log_{4}{1}-\frac{1}{7}\log_{4}{2} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 11. (1 pkt) (Numer zadania: pp-11806)
[ ⇒ Rozwiąż ]
Podpunkt 11.1 (1 pkt)
Wartość wyrażenia
\frac{2^{-1}}{\left(-\frac{1}{4}\right)^{-2}}\cdot 16 jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 12. (1 pkt) (Numer zadania: pp-11828)
[ ⇒ Rozwiąż ]
Podpunkt 12.1 (1 pkt)
Liczba
\left(2^{-2.8}\cdot 2^{\frac{4}{5}}}\right)^{\frac{1}{2}} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 13. (1 pkt) (Numer zadania: pp-11829)
[ ⇒ Rozwiąż ]
Podpunkt 13.1 (1 pkt)
Liczba
\log_{5}{1250}-\log_{5}{2} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 14. (1 pkt) (Numer zadania: pp-11830)
[ ⇒ Rozwiąż ]
Podpunkt 14.1 (1 pkt)
Pan Grzegorz wpłacił do banku pewną kwotę na lokatę dwuletnią. Po każdym rocznym okresie
oszczędzania bank doliczał odsetki w wysokości
25\% od kwoty bieżącego
kapitału znajdującego się na lokacie. Po dwóch latach oszczędzania pan Grzegorz odebrał z tego
banku wraz z odsetkami kwotę
5000.00 zł (bez uwzględnienia podatków).
Kwota K wpłacona przez pana Grzegorza na tę lokatę była równa:
Odpowiedź:
K\ [zl]=
(wpisz liczbę całkowitą)
Zadanie 15. (1 pkt) (Numer zadania: pp-11832)
[ ⇒ Rozwiąż ]
Podpunkt 15.1 (0.2 pkt)
Przedział liczbowy
(-14, 2) jest rozwiązaniem nierówności
|x-a|\ ...\ b .
Wskaż brakujący znak nierówności:
Odpowiedzi:
A. \geqslant
B. \lessdot
C. >
D. \leqslant
Podpunkt 15.2 (0.8 pkt)
Odpowiedzi:
Zadanie 16. (1 pkt) (Numer zadania: pp-11851)
[ ⇒ Rozwiąż ]
Podpunkt 16.1 (1 pkt)
Liczba
2\log_{4}{2}+2\log_{4}{8} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 17. (1 pkt) (Numer zadania: pp-11852)
[ ⇒ Rozwiąż ]
Podpunkt 17.1 (1 pkt)
Cena działki po kolejnych dwóch obniżkach, za każdym razem o
10\%
w odniesieniu do ceny obowiązującej w danym momencie, jest równa
64719.00 zł.
Cena C w złotych tej działki przed obiema obniżkami była, w zaokrągleniu do 1 zł, równa:
Odpowiedź:
C\ [zl]=
(wpisz liczbę całkowitą)
Zadanie 18. (1 pkt) (Numer zadania: pp-11853)
[ ⇒ Rozwiąż ]
Podpunkt 18.1 (1 pkt)
Liczba
7^{6+\frac{1}{4}} jest równa liczbie
\sqrt[m]{7^n} .
Podaj liczby m i n .
Odpowiedzi:
Zadanie 19. (1 pkt) (Numer zadania: pp-11878)
[ ⇒ Rozwiąż ]
Podpunkt 19.1 (1 pkt)
Liczba
\sqrt{162}:\sqrt[3]{125} jest równa:
Odpowiedź:
Zadanie 20. (1 pkt) (Numer zadania: pp-11879)
[ ⇒ Rozwiąż ]
Podpunkt 20.1 (1 pkt)
Liczba
\frac{2^{-3}\cdot3^{-1}\cdot4^0}{2^{-1}\cdot3^{-6}\cdot4^{-1}} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 21. (1 pkt) (Numer zadania: pp-11880)
[ ⇒ Rozwiąż ]
Podpunkt 21.1 (1 pkt)
Liczba dwukrotnie większa od
\log{2}+\log{5} jest równa
\log x .
Podaj liczbę x :
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Zadanie 22. (1 pkt) (Numer zadania: pp-11881)
[ ⇒ Rozwiąż ]
Podpunkt 22.1 (1 pkt)
30\% liczby
x jest o
2821 mniejsze od liczby
x .
Liczba x jest równa:
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Zadanie 23. (1 pkt) (Numer zadania: pp-11907)
[ ⇒ Rozwiąż ]
Podpunkt 23.1 (1 pkt)
Liczba
\frac{8^{-35}}{2^{19}} jest równa
4^n .
Podaj liczbę n .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 24. (1 pkt) (Numer zadania: pp-11908)
[ ⇒ Rozwiąż ]
Podpunkt 24.1 (1 pkt)
Liczba
\log_{2}{32}-\log_{2}{16} jest równa:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Zadanie 25. (1 pkt) (Numer zadania: pp-11911)
[ ⇒ Rozwiąż ]
Podpunkt 25.1 (1 pkt)
Cenę
x (w złotych) pewnego towaru obniżono najpierw o
10\% , a następnie obniżono o
50\%
w odniesieniu do ceny obowiązującej w danym momencie.
Zapisz cenę towaru po obydwu tych obniżkach w postaci
p\cdot x .
Podaj liczbę p zaokrągloną do dwóch miejsc po przecinku.
Odpowiedź:
p=
(liczba zapisana dziesiętnie)
Zadanie 26. (1 pkt) (Numer zadania: pp-11936)
[ ⇒ Rozwiąż ]
Podpunkt 26.1 (1 pkt)
Wartość wyrażenia
\left(1+5\cdot 2^{-1}\right)^{-3} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 27. (1 pkt) (Numer zadania: pp-11937)
[ ⇒ Rozwiąż ]
Podpunkt 27.1 (1 pkt)
Wartość wyrażenia
2\log_{5}{5}+5-\log_{5}{5^3} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 28. (1 pkt) (Numer zadania: pp-11947)
[ ⇒ Rozwiąż ]
Podpunkt 28.1 (0.2 pkt)
Zbiór
(-\infty, -18)\cup(4,+\infty) jest rozwiązaniem nierówności
postaci
|x-a|\ ...\ b .
Wskaż znak tej nierówności:
Odpowiedzi:
A. >
B. \leqslant
C. \lessdot
D. \geqslant
Podpunkt 28.2 (0.8 pkt)
Odpowiedzi:
Zadanie 29. (1 pkt) (Numer zadania: pp-11956)
[ ⇒ Rozwiąż ]
Podpunkt 29.1 (1 pkt)
Zapisz liczbę
\left(7^{6}\cdot 7^{\frac{1}{2}}\right)^{\frac{1}{13}} w postaci
\sqrt[m]{7^n} .
Podaj ułamek \frac{m}{n} .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 30. (1 pkt) (Numer zadania: pp-11957)
[ ⇒ Rozwiąż ]
Podpunkt 30.1 (1 pkt)
Pan Nowak kupił obligacje Skarbu Państwa za
40000 zł
oprocentowane
3\% w skali roku. Odsetki są naliczane
i kapitalizowane co rok.
Wartość obligacji kupionych przez pana Nowaka, w zaokrągleniu do pełnych groszy, będzie po n=4
latach równa:
Odpowiedź:
K_n=
(liczba zapisana dziesiętnie)
Zadanie 31. (1 pkt) (Numer zadania: pp-11980)
[ ⇒ Rozwiąż ]
Podpunkt 31.1 (1 pkt)
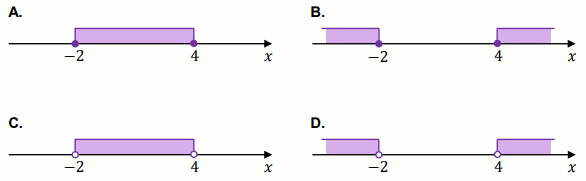
Dana jest nierówność
|x-1|\geqslant 3 .
Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb
rzeczywistych spełniających powyższą nierówność?
Odpowiedzi:
Zadanie 32. (1 pkt) (Numer zadania: pp-11981)
[ ⇒ Rozwiąż ]
Podpunkt 32.1 (1 pkt)
Liczba
\left(\frac{1}{16}\right)^{7}\cdot 8^{14} jest równa
2^n .
Podaj liczbę n .
Odpowiedź:
n=
(wpisz liczbę całkowitą)
Zadanie 33. (1 pkt) (Numer zadania: pp-11982)
[ ⇒ Rozwiąż ]
Podpunkt 33.1 (1 pkt)
Liczba
\log_{\sqrt{2}}{16} jest równa:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Zadanie 34. (1 pkt) (Numer zadania: pp-12002)
[ ⇒ Rozwiąż ]
Podpunkt 34.1 (1 pkt)
Liczba
2^{-1}\cdot 32^{\frac{6}{5}} jest równa
2^k , gdzie
k\in\mathbb{Z} .
Podaj liczbę k .
Odpowiedź:
k=
(wpisz liczbę całkowitą)
Zadanie 35. (1 pkt) (Numer zadania: pp-12003)
[ ⇒ Rozwiąż ]
Podpunkt 35.1 (1 pkt)
Liczba
\log_{3}{\frac{81}{2}}+\log_{3}{\frac{2}{243}} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 36. (1 pkt) (Numer zadania: pp-12005)
[ ⇒ Rozwiąż ]
Podpunkt 36.1 (1 pkt)
Klient wpłacił do banku na lokatę
n=5 letnią kwotę w wysokości
1000 zł.
Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości
8\% od kwoty bieżącego kapitału znajdującego się na
lokacie – zgodnie z procentem składanym.
Po n=5 latach oszczędzania w tym banku kwota w złotych na lokacie
(bez uwzględniania podatków) zaokrąglona do dwóch miejsc po przecinku jest równa:
Odpowiedź:
K_n=
(liczba zapisana dziesiętnie)
Zadanie 37. (1 pkt) (Numer zadania: pp-12024)
[ ⇒ Rozwiąż ]
Podpunkt 37.1 (1 pkt)
Liczba
(\sqrt{35}-\sqrt{7})^2-2\sqrt{5} jest równa:
Odpowiedź:
Wpisz odpowiedź:
+
\cdot
√
(wpisz trzy liczby całkowite)
Zadanie 38. (1 pkt) (Numer zadania: pp-12025)
[ ⇒ Rozwiąż ]
Podpunkt 38.1 (1 pkt)
Liczba
2\log_{5}{16}-6\log_{5}{\frac{1}{2}} jest równa
a\log_{5}{2} .
Podaj liczbę a .
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Zadanie 39. (1 pkt) (Numer zadania: pp-12026)
[ ⇒ Rozwiąż ]
Podpunkt 39.1 (1 pkt)
Medyczna maseczka ochronna wielokrotnego użytku z wymiennymi filtrami wskutek podwyżki
zdrożała o
25\% i kosztuje obecnie
59.10 zł.
Cena maseczki w złotych przed podwyżką była równa:
Odpowiedź:
c\ [zl]=
(liczba zapisana dziesiętnie)
Zadanie 40. (1 pkt) (Numer zadania: pp-12027)
[ ⇒ Rozwiąż ]
Podpunkt 40.1 (1 pkt)
Liczba
\left(\sqrt[2]{b}\cdot\sqrt[6]{b}\right)^{\frac{1}{4}} jest równa
b^{p} .
Podaj wykładnik potęgi p .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 41. (1 pkt) (Numer zadania: pp-12052)
[ ⇒ Rozwiąż ]
Podpunkt 41.1 (1 pkt)
Liczba
100^{-12}\cdot (0,1)^{8} jest równa
10^{p} .
Podaj wykładnik potęgi p .
Odpowiedź:
p=
(wpisz liczbę całkowitą)
Zadanie 42. (1 pkt) (Numer zadania: pp-12053)
[ ⇒ Rozwiąż ]
Podpunkt 42.1 (1 pkt)
Liczba
141 stanowi
150\%
liczby
c .
Wtedy liczba c jest równa:
Odpowiedź:
c=
(wpisz liczbę całkowitą)
Zadanie 43. (1 pkt) (Numer zadania: pp-12054)
[ ⇒ Rozwiąż ]
Podpunkt 43.1 (1 pkt)
Rozważamy przedziały liczbowe
(-\infty, 11) i
[-11+\infty) .
Ile jest wszystkich liczb całkowitych, które należą jednocześnie do obu
rozważanych przedziałów?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Zadanie 44. (1 pkt) (Numer zadania: pp-12055)
[ ⇒ Rozwiąż ]
Podpunkt 44.1 (1 pkt)
Liczba
14\log_{7}{\sqrt{7}}+\log_{7}{7^{2}} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 45. (1 pkt) (Numer zadania: pp-12056)
[ ⇒ Rozwiąż ]
Podpunkt 45.1 (1 pkt)
Różnica
0,(6)-\frac{20}{33} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 46. (1 pkt) (Numer zadania: pp-12080)
[ ⇒ Rozwiąż ]
Podpunkt 46.1 (1 pkt)
Liczba
\sqrt{2}\cdot(\sqrt{2}-\sqrt{11})+\sqrt{11}\cdot(\sqrt{2}-\sqrt{11}) jest równa
a+b\sqrt{c} .
Podaj liczby a , b i c .
Odpowiedź:
a+b\sqrt{c}=
+
\cdot
√
(wpisz trzy liczby całkowite)
Zadanie 47. (1 pkt) (Numer zadania: pp-12081)
[ ⇒ Rozwiąż ]
Podpunkt 47.1 (1 pkt)
Liczba
\left(7^{\frac{5}{6}}\cdot 7^{\frac{1}{2}}\right)^{\frac{2}{3}} jest równa
p^c , gdzie
p jest liczbą pierwszą.
Podaj wykładnik potęgi c .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 48. (1 pkt) (Numer zadania: pp-12082)
[ ⇒ Rozwiąż ]
Podpunkt 48.1 (1 pkt)
Niech
\log_{5}{2=c} .
Wtedy
\log_{5}{250} jest równy
c+m .
Podaj liczbę m .
Odpowiedź:
m=
(wpisz liczbę całkowitą)
Zadanie 49. (1 pkt) (Numer zadania: pp-12083)
[ ⇒ Rozwiąż ]
Podpunkt 49.1 (1 pkt)
Cenę drukarki obniżono o
10\% , a następnie nową cenę obniżono
o
50\% .
W wyniku obu tych zmian cena drukarki zmniejszyła się w stosunku do ceny sprzed obu obniżek o
p\% .
Podaj liczbę p .
Odpowiedź:
p\ [\%]=
(wpisz liczbę całkowitą)
Zadanie 50. (1 pkt) (Numer zadania: pp-12107)
[ ⇒ Rozwiąż ]
Podpunkt 50.1 (1 pkt)
Liczba
49^{-11}\cdot 7^{6} jest równa
7^n .
Podaj wykładnik potęgi n .
Odpowiedź:
n=
(wpisz liczbę całkowitą)
Zadanie 51. (1 pkt) (Numer zadania: pp-12108)
[ ⇒ Rozwiąż ]
Podpunkt 51.1 (1 pkt)
Liczba
x stanowi
15\%
liczby dodatniej
y . Wynika stąd, że liczba
y
to
p\% liczby
x .
Liczba p zaokrąglona do dwóch miejsc po przecinku jest równa:
Odpowiedź:
p=
(liczba zapisana dziesiętnie)
Zadanie 52. (1 pkt) (Numer zadania: pp-12109)
[ ⇒ Rozwiąż ]
Podpunkt 52.1 (1 pkt)
Liczba
\log_{14}{343}+3\log_{14}{2} jest równa:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Zadanie 53. (1 pkt) (Numer zadania: pp-12136)
[ ⇒ Rozwiąż ]
Podpunkt 53.1 (1 pkt)
Liczbę
\sqrt[3]{343\cdot\sqrt{7}} można
zapisać w postaci
p^a , gdzie
p
jest liczbą pierwszą, a
a liczbą wymierną.
Podaj liczby p i a .
Odpowiedzi:
Zadanie 54. (1 pkt) (Numer zadania: pp-12137)
[ ⇒ Rozwiąż ]
Podpunkt 54.1 (1 pkt)
Liczba
2\log{3}+3\log{5} jest równa
\log{m} .
Podaj liczbę m .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 55. (1 pkt) (Numer zadania: pp-12138)
[ ⇒ Rozwiąż ]
Podpunkt 55.1 (1 pkt)
W zestawie
250 liczb występują jedynie liczby
4
i
2 . Liczba
4 występuje
166 razy,
a liczba
2 występuje
84 razy. Przyjęto przybliżenie średniej
arytmetycznej
\overline{x} zestawu tych wszystkich liczb do liczby
3 .
Błąd bezwzględny tego przybliżenia, czyli liczba |\overline{x}-3| , jest równy:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 56. (1 pkt) (Numer zadania: pp-12139)
[ ⇒ Rozwiąż ]
Podpunkt 56.1 (1 pkt)
Na początku miesiąca komputer kosztował
5400 zł. W drugiej dekadzie
tego miesiąca cenę komputera obniżono o
30\% , a w trzeciej dekadzie
cena tego komputera została jeszcze raz obniżona, tym razem o
50\% .
Innych zmian ceny tego komputera w tym miesiącu już nie było.
Cena komputera na koniec miesiąca była równa:
Odpowiedź:
Cena\ koncowa\ [zl]=
(liczba zapisana dziesiętnie)
Zadanie 57. (1 pkt) (Numer zadania: pp-12141)
[ ⇒ Rozwiąż ]
Podpunkt 57.1 (1 pkt)
Liczba
w=\log_{\sqrt{2}}{16^{12}} jest równa:
Odpowiedź:
w=
(wpisz liczbę całkowitą)
Zadanie 58. (1 pkt) (Numer zadania: pp-12142)
[ ⇒ Rozwiąż ]
Podpunkt 58.1 (1 pkt)
Masę planety równą
4.984\cdot 10^{36} kg przybliżono do
5\cdot 10^{36} kg. Błąd bezwzględny
B_{bzw} tego
przybliżenia równy
|4.984\cdot 10^{36}-5\cdot 10^{36}| jest
równy
m\cdot 10^c , gdzie mantysa
m\in(0,1] i
cecha
c\in\mathbb{N} .
Podaj liczbę m .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 59. (1 pkt) (Numer zadania: pp-12144)
[ ⇒ Rozwiąż ]
Podpunkt 59.1 (1 pkt)
Liczba
\frac{2^{76}\cdot 3^{96}}{36^{24}} jest równa
2^m\cdot 3^n .
Podaj liczby m i n .
Odpowiedzi:
Zadanie 60. (1 pkt) (Numer zadania: pp-12145)
[ ⇒ Rozwiąż ]
Podpunkt 60.1 (1 pkt)
Cenę
x pewnego towaru obniżono o
36\% i otrzymano
cenę
y .
Aby przywrócić cenę
x , nową cenę
y należy podnieść o
d\% .
Podaj liczbę d .
Odpowiedź:
d=
(liczba zapisana dziesiętnie)
Zadanie 61. (1 pkt) (Numer zadania: pp-12146)
[ ⇒ Rozwiąż ]
Podpunkt 61.1 (1 pkt)
Niech
a=4 i
b=-4 . Wartość wyrażenia
a^b-b^a jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 62. (1 pkt) (Numer zadania: pp-12147)
[ ⇒ Rozwiąż ]
Podpunkt 62.1 (1 pkt)
Liczba
16^{14}\cdot 64^{28} jest równa
4^k .
Podaj liczbę k .
Odpowiedź:
k=
(wpisz liczbę całkowitą)
Zadanie 63. (1 pkt) (Numer zadania: pp-12148)
[ ⇒ Rozwiąż ]
Podpunkt 63.1 (1 pkt)
Wartość wyrażenia
w=\log_{16}{64}+10\log_{16}{4} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 64. (1 pkt) (Numer zadania: pp-12149)
[ ⇒ Rozwiąż ]
Podpunkt 64.1 (1 pkt)
Dane są dwa koła. Promień pierwszego koła jest większy od promienia drugiego koła o
32\% . Wynika stąd, że pole pierwszego koła jest większe od pola drugiego
koła o
d\% .
Podaj liczbę d .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 65. (1 pkt) (Numer zadania: pp-12151)
[ ⇒ Rozwiąż ]
Podpunkt 65.1 (1 pkt)
Liczba
\log_{2\sqrt{7}}{28} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 66. (1 pkt) (Numer zadania: pp-12153)
[ ⇒ Rozwiąż ]
Podpunkt 66.1 (1 pkt)
75\% liczby
a jest równe
210 , a
75\% liczby
b jest równe
108 .
Oblicz różnicę a-b .
Odpowiedź:
a-b=
(wpisz liczbę całkowitą)
Zadanie 67. (1 pkt) (Numer zadania: pp-12154)
[ ⇒ Rozwiąż ]
Podpunkt 67.1 (1 pkt)
Liczba
\frac{\log_{4}{64}}{\log_{4}{\sqrt{64}}}
jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 68. (1 pkt) (Numer zadania: pp-12155)
[ ⇒ Rozwiąż ]
Podpunkt 68.1 (1 pkt)
Podaj liczbę cyfr liczby
2^{272}\cdot 5^{270} :
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Zadanie 69. (1 pkt) (Numer zadania: pp-12156)
[ ⇒ Rozwiąż ]
Podpunkt 69.1 (1 pkt)
W pewnym banku prowizja od udzielanych kredytów hipotecznych przez cały styczeń była równa
20\% . Na początku lutego ten bank obniżył wysokość prowizji od wszystkich kredytów
o
k=16 punktów procentowych. Oznacza to, że prowizja od kredytów hipotecznych
w tym banku zmniejszyła się o
p\% .
Podaj liczbę p .
Odpowiedź:
p=
(wpisz liczbę całkowitą)
Zadanie 70. (1 pkt) (Numer zadania: pp-12158)
[ ⇒ Rozwiąż ]
Podpunkt 70.1 (1 pkt)
Cena pewnego towaru w wyniku obniżki o
20\% zmniejszyła się o
1060 zł.
Ten towar po tej obniżce kosztował:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Zadanie 71. (1 pkt) (Numer zadania: pp-12159)
[ ⇒ Rozwiąż ]
Podpunkt 71.1 (1 pkt)
Liczba
\sqrt[4]{\sqrt[6]{2^7}} jest równa
2^{a} .
Podaj liczbę a .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 72. (1 pkt) (Numer zadania: pp-12342)
[ ⇒ Rozwiąż ]
Podpunkt 72.1 (1 pkt)
Podaj liczbę wszystkich
całkowitych rozwiązań nierówności
|x+4| < 5 :
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
Zadanie 73. (1 pkt) (Numer zadania: pp-12343)
[ ⇒ Rozwiąż ]
Podpunkt 73.1 (1 pkt)
Liczba
\left(\frac{1}{16}\right)^{-0,5} , zaokrąglona
do dwóch miejsc po przecinku jest równa
m .
Podaj liczbę m :
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 74. (2 pkt) (Numer zadania: pp-12344)
[ ⇒ Rozwiąż ]
Podpunkt 74.1 (1 pkt)
Liczba
\log_{2}{36}+\log_{2}{25} jest równa
\log_{2}{m} .
Podaj liczbę m :
Odpowiedź:
m=
(wpisz liczbę całkowitą)
Podpunkt 74.2 (1 pkt)
Liczba
\log_{3}{25}+\log_{3}{49} jest równa
2\log_{3}{m} .
Podaj liczbę m :
Odpowiedź:
m=
(wpisz liczbę całkowitą)
Zadanie 75. (1 pkt) (Numer zadania: pp-12364)
[ ⇒ Rozwiąż ]
Podpunkt 75.1 (1 pkt)
Liczby
x_1 i
x_2 są różnymi rozwiązaniami
równania
|x-8|=10 .
Podaj sumę x_1+x_2 :
Odpowiedź:
x_1+x_2=
(wpisz liczbę całkowitą)
Zadanie 76. (1 pkt) (Numer zadania: pp-12365)
[ ⇒ Rozwiąż ]
Podpunkt 76.1 (1 pkt)
Zapisz liczbę
\left(\sqrt[5]{7}\cdot\frac{1}{7}\right)^{-3} w postaci potęgi
7^m .
Podaj wykładnik m tej potęgi:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 77. (1 pkt) (Numer zadania: pp-12366)
[ ⇒ Rozwiąż ]
Podpunkt 77.1 (1 pkt)
Dla każdej dodatniej liczby rzeczywistej
x i dla każdej dodatniej liczby
rzeczywistej
y wartość wyrażenia
6\log_{2}{x}+5\log_{2}{4} jest równa wartości wyrażenia
\log_{2}{ax^n} .
Podaj liczby a i n .
Odpowiedzi:
Zadanie 78. (1 pkt) (Numer zadania: pp-12367)
[ ⇒ Rozwiąż ]
Podpunkt 78.1 (1 pkt)
Pani Aniela wpłaciła do banku kwotę
75000 zł na lokatę dwuletnią.
Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości
p\%
w skali roku od kwoty bieżącego kapitału znajdującego się na lokacie – zgodnie z procentem składanym.
Na koniec okresu oszczędzania kwota na tej lokacie była równa
92407.50 zł
wraz z odsetkami (bez uwzględniania podatków).
Oprocentowanie lokaty w skali roku w procentach było równe:
Odpowiedź:
p\ [\%]=
(liczba zapisana dziesiętnie)
Zadanie 79. (1 pkt) (Numer zadania: pp-12383)
[ ⇒ Rozwiąż ]
Podpunkt 79.1 (1 pkt)
Liczba
\frac{5^{22}+5^{23}+5^{24}}{5^{22}}
jest równa:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Zadanie 80. (1 pkt) (Numer zadania: pp-12384)
[ ⇒ Rozwiąż ]
Podpunkt 80.1 (1 pkt)
Liczba
\log_{2}{5000}-4\log_{2}{5} jest równa:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Zadanie 81. (1 pkt) (Numer zadania: pp-12402)
[ ⇒ Rozwiąż ]
Podpunkt 81.1 (1 pkt)
Liczby
x_1 i
x_2 są różnymi rozwiązaniami
równania
|x-8|=10 .
Iloczyn x_1\cdot x_2 jest równy:
Odpowiedź:
x_1\cdot x_2=
(wpisz liczbę całkowitą)
Zadanie 82. (1 pkt) (Numer zadania: pp-12403)
[ ⇒ Rozwiąż ]
Podpunkt 82.1 (1 pkt)
Liczba
2^{7}\cdot \sqrt[5]{32^{6}} jest równa
2^m .
Podaj liczbę m .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 83. (1 pkt) (Numer zadania: pp-12404)
[ ⇒ Rozwiąż ]
Podpunkt 83.1 (1 pkt)
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
T/N : 1+\log_{2}{4}=\log_{2}{32}
T/N : 2+\log_{2}{4}=\log_{2}{16}
Zadanie 84. (1 pkt) (Numer zadania: pp-12424)
[ ⇒ Rozwiąż ]
Podpunkt 84.1 (1 pkt)
Liczba
w=\log_{2}{5}-\log_{2}{625} jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 85. (1 pkt) (Numer zadania: pp-12423)
[ ⇒ Rozwiąż ]
Podpunkt 85.1 (1 pkt)
Zapisz liczbę
\sqrt[3]{135}+\sqrt[3]{320} w postaci
a\sqrt[3]{b} , gdzie
a,b\in\mathbb{Z} i
b
jest najmniejsze możliwe.
Podaj liczby a i b .
Odpowiedzi:
Zadanie 86. (1 pkt) (Numer zadania: pp-12422)
[ ⇒ Rozwiąż ]
Podpunkt 86.1 (1 pkt)
Zapisz liczbę
\frac{25^{-7}}{625^{-2}} w postaci
potęgi
5^n .
Podaj wykładnik n tej potęgi.
Odpowiedź:
n=
(wpisz liczbę całkowitą)
Zadanie 87. (1 pkt) (Numer zadania: pp-12421)
[ ⇒ Rozwiąż ]
Podpunkt 87.1 (1 pkt)
Liczba
\left|\sqrt{7}-5\right|+\left|\sqrt{7}-1\right| jest równa:
Odpowiedź:
Wpisz odpowiedź:
\cdot √
(wpisz dwie liczby całkowite)
Masz pytania? Napisz: k42195@poczta.fm