Liczby rzeczywiste
Zadania z matur CKE dla liceum ogólnokształcącego - poziom rozszerzony
- dodawanie, odejmowanie, mnożenie, dzielenie, potęgowanie, pierwiastkowanie, logarytmowanie w zbiorze liczb rzeczywistych
- własności pierwiastków dowolnego stopnia, w tym pierwiastków stopnia nieparzystego z liczb ujemnych
- związek pierwiastkowania z potęgowaniem oraz prawa działań na potęgach i pierwiastkach
- własności monotoniczności potęgowania, w szczególności własności: jeśli x\lessdot y i a>1, to a^x\lessdot a^y, zaś jeśli x\lessdot y i a\in(0,1), to a^x> a^y
- przedział liczbowy, przedziały na osi liczbowej
- interpretacja geometryczna i algebraiczna wartości bezwzględnej, równania i nierówności typu |x+4|=5, |x-2|\lessdot 3, |x+3|\geqslant 4
- własności potęgowania i pierwiastkowania w sytuacjach praktycznych, w tym do obliczania procentów składanych, zysków z lokat i kosztów kredytów
- związek logarytmowania z potęgowaniem, logarytm iloczynu, logarytm ilorazu i logarytm potęgi
| Zadanie 1. (2 pkt) (Numer zadania: pr-21154) | [ ⇒ Rozwiąż ] |
Podpunkt 1.1 (2 pkt)
W chwili początkowej (t=0) masa substancji jest równa
4 gram. Wskutek rozpadu cząsteczek tej substancji jej
masa się zmniejsza. Po każdej kolejnej dobie ubywa 18\% masy,
jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej t\geqslant 0
funkcja m(t) określa masę substancji w gramach po
t pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór
funkcji m(t).
Oblicz, po ilu pełnych dobach masa tej substancji będzie po raz pierwszy mniejsza od 1,5 grama.
Odpowiedź:
t=
(wpisz liczbę całkowitą)
| Zadanie 2. (2 pkt) (Numer zadania: pr-21160) | [ ⇒ Rozwiąż ] |
Podpunkt 2.1 (1 pkt)
Dane są liczby:
a=25^{\log_{5}{8}} oraz
b=\frac{\log_{4}{2029}}{\log_{256}{2029}}.
Podaj liczbę a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 2.2 (1 pkt)
Podaj liczbę b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 3. (2 pkt) (Numer zadania: pr-21166) | [ ⇒ Rozwiąż ] |
Podpunkt 3.1 (2 pkt)
W chwili początkowej (t=0) filiżanka z gorącą kawą znajduje się
w pokoju, a temperatura tej kawy jest równa 74^{\circ}C.
Temperatura w pokoju (temperatura otoczenia) jest stała i równa
14^{\circ}C. Temperatura T tej kawy
zmienia się w czasie zgodnie z zależnością T(t)=(T_p-T_z)\cdot k^{-t}+T_z
dla t\geqslant 0 gdzie:
- T – temperatura kawy wyrażona w stopniach Celsjusza,
- t – czas wyrażony w minutach, liczony od chwili początkowej,
- T_p – temperatura początkowa kawy wyrażona w stopniach Celsjusza,
- T_z – temperatura otoczenia wyrażona w stopniach Celsjusza,
- k – stała charakterystyczna dla danej cieczy.
Oblicz temperaturę tej kawy po następnych pięciu minutach.
Odpowiedź:
| T(15)= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 4. (2 pkt) (Numer zadania: pr-21171) | [ ⇒ Rozwiąż ] |
Podpunkt 4.1 (2 pkt)
W chwili początkowej (t=0) zainicjowano pewną reakcję chemiczną,
w której brał udział związek A. W wyniku tej reakcji masa
m związku A zmieniała się w czasie
zgodnie z zależnością m(t)=a\cdot 2^{-0.25\cdot t}+b dla
t\geqslant 0 gdzie:
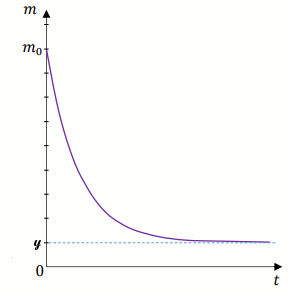
- m – masa związku A wyrażona w gramach,
- t – czas wyrażony w sekundach (liczony od chwili t=0),
- a,b – współczynniki liczbowe.

Oblicz, po ilu sekundach (licząc od chwili zainicjowania tej reakcji) przereagowało \frac{4}{9} masy początkowej tego związku.
Odpowiedź:
t\ [s]=
(wpisz liczbę całkowitą)
| Zadanie 5. (2 pkt) (Numer zadania: pr-21181) | [ ⇒ Rozwiąż ] |
Podpunkt 5.1 (2 pkt)
Oblicz \frac{\log_{5}{7}\cdot\log_{49}{125}}{\log_{3}{\sqrt[7]{9}}}.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 6. (2 pkt) (Numer zadania: pr-21183) | [ ⇒ Rozwiąż ] |
Podpunkt 6.1 (2 pkt)
Dane są liczby a=\log_{5}{3} oraz b=\log_{3}{4}.
Liczbę \log_{25}{16^{2}} zapisz w postaci
m\cdot a\cdot b.
Podaj liczbę m.
Odpowiedź:
| m= | |
| Zadanie 7. (3 pkt) (Numer zadania: pr-21187) | [ ⇒ Rozwiąż ] |
Podpunkt 7.1 (3 pkt)
Niech \log_{3}{12}=c. Zapisz wyrażenie
\frac{6}{c-1} w postaci \log_{a}{b}, gdzie
a jest liczbą pierwszą i b\in\mathbb{Z}.
Podaj liczbę b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 8. (3 pkt) (Numer zadania: pr-21191) | [ ⇒ Rozwiąż ] |
Podpunkt 8.1 (3 pkt)
Niech \log_{3}{4}=c. Zapisz wyrażenie
\frac{2c+2}{c} w postaci \log_{2}{a}.
Podaj liczbę a.
Odpowiedź:
Wpisz odpowiedź:
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)