Równania i nierówności
Zadania z matur CKE dla liceum ogólnokształcącego - poziom podstawowy
Uczeń:
- przekształca równania i nierówności w sposób równoważny;
- interpretuje równania i nierówności sprzeczne oraz tożsamościowe;
- rozwiązuje nierówności liniowe z jedną niewiadomą;
- rozwiązuje równania i nierówności kwadratowe;
- rozwiązuje równania wielomianowe, które dają się doprowadzić do równania kwadratowego, w szczególności równania dwukwadratowe;
- rozwiązuje równania wielomianowe postaci W(x)=0 dla wielomianów doprowadzonych do postaci iloczynowej lub takich, które dają się doprowadzić do postaci iloczynowej metodą wyłączania wspólnego czynnika przed nawias lub metodą grupowania;
- rozwiązuje równania wymierne postaci \frac{V(x)}{W(x)}=0, gdzie wielomiany V(x) i W(x) są zapisane w postaci iloczynowej.
| Zadanie 1. (1 pkt) (Numer zadania: pp-11761) | [ ⇒ Rozwiąż ] |
Podpunkt 1.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności
-2(x+13)\leqslant\frac{-8-x}{3}
jest przedział postaci:
Odpowiedzi:
| A. (a,+\infty) | B. [-\infty, a) |
| C. (-\infty, a] | D. [a,+\infty) |
Podpunkt 1.2 (0.8 pkt)
Podaj liczbę a.
Odpowiedź:
| a= | |
| Zadanie 2. (1 pkt) (Numer zadania: pp-11762) | [ ⇒ Rozwiąż ] |
Podpunkt 2.1 (0.4 pkt)
Jednym z rozwiązań równania
\sqrt{8}\cdot (x^2-5)(x-4)=0
jest liczba:
Odpowiedzi:
| A. -5 | B. -4 |
| C. 5 | D. 25 |
| E. -25 | F. \sqrt{5} |
Podpunkt 2.2 (0.6 pkt)
Podaj największe rozwiązanie tego równania.
Odpowiedź:
x_{max}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 3. (1 pkt) (Numer zadania: pp-11763) | [ ⇒ Rozwiąż ] |
Podpunkt 3.1 (1 pkt)
Równanie
\frac{(x+9)(x+3)^2}{(x-3)(x+9)^2}=0:
Odpowiedzi:
| A. ma dokładnie jedno rozwiązanie równe 9 | B. ma dokładnie jedno rozwiązanie równe -3 |
| C. ma dwa rozwiązania równe -9 oraz 3 | D. nie ma rozwiązania |
| Zadanie 4. (1 pkt) (Numer zadania: pp-11784) | [ ⇒ Rozwiąż ] |
Podpunkt 4.1 (1 pkt)
Równanie
\frac{(x^2+4x)(x-2)}{x^2-4}=0
w zbiorze liczb rzeczywistych ma dokładnie:
Odpowiedzi:
| A. jedno rozwiązanie | B. dwa rozwiązania |
| C. trzy rozwiązania | D. cztery rozwiązania |
| Zadanie 5. (1 pkt) (Numer zadania: pp-11809) | [ ⇒ Rozwiąż ] |
Podpunkt 5.1 (1 pkt)
Równanie \frac{(x^2+5x)(x^2+1)}{x^2-4}=0 w zbiorze
liczb rzeczywistych ma dokładnie:
Odpowiedzi:
| A. cztery rozwiązanie | B. trzy rozwiązanie |
| C. jedno rozwiązanie | D. dwa rozwiązania |
| Zadanie 6. (1 pkt) (Numer zadania: pp-11855) | [ ⇒ Rozwiąż ] |
Podpunkt 6.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności \frac{4}{7}-\frac{x}{5}>\frac{x}{7},
jest przedział postaci:
Odpowiedzi:
| A. [a,+\infty) | B. (a,+\infty) |
| C. (-\infty,a] | D. (-\infty,a) |
Podpunkt 6.2 (0.8 pkt)
Podaj liczbę a:
Odpowiedź:
| a= | |
| Zadanie 7. (1 pkt) (Numer zadania: pp-11856) | [ ⇒ Rozwiąż ] |
Podpunkt 7.1 (1 pkt)
Suma wszystkich rozwiązań równania 10x(x^2-9)(x-4)=0 jest równa:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) (Numer zadania: pp-11885) | [ ⇒ Rozwiąż ] |
Podpunkt 8.1 (1 pkt)
Równanie (x^2-81)(x^2+5)=0 ma dokładnie
Odpowiedzi:
| A. cztery rozwiązania | B. jedno rozwiązanie |
| C. dwa rozwiązania | D. trzy rozwiązania |
| Zadanie 9. (1 pkt) (Numer zadania: pp-11909) | [ ⇒ Rozwiąż ] |
Podpunkt 9.1 (1 pkt)
Jednym z rozwiązań równania 10(x-3)-x^2(x-3)=0
jest liczba:
Odpowiedzi:
| A. 1 | B. 6 |
| C. -3 | D. 7 |
| E. 3 | F. -1 |
| Zadanie 10. (1 pkt) (Numer zadania: pp-11912) | [ ⇒ Rozwiąż ] |
Podpunkt 10.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności \frac{8x-3}{4}>-3x
jest przedział postaci:
Odpowiedzi:
| A. \left(a,+\infty\right) | B. \left(-\infty,a] |
| C. \left[a,+\infty\right) | D. \left(-\infty,a) |
Podpunkt 10.2 (0.8 pkt)
Podaj liczbę a.
Odpowiedź:
| a= | |
| Zadanie 11. (1 pkt) (Numer zadania: pp-11913) | [ ⇒ Rozwiąż ] |
Podpunkt 11.1 (1 pkt)
Suma wszystkich rozwiązań równania
(3x-2)(3x-1)(x+1)=0 jest równa:
Odpowiedź:
| suma= | |
| Zadanie 12. (1 pkt) (Numer zadania: pp-11934) | [ ⇒ Rozwiąż ] |
Podpunkt 12.1 (1 pkt)
Punkt A=(1,2) należy do wykresu funkcji
f, określonej wzorem
f(x)=(m^2+16m+61)x^3-m^2-15m-55
dla każdej liczby rzeczywistej x.
Wtedy liczba m jest równa:
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 13. (1 pkt) (Numer zadania: pp-11941) | [ ⇒ Rozwiąż ] |
Podpunkt 13.1 (1 pkt)
Równanie \frac{(x^2+4x)(x-3)(x-4)}{x^2-16}=0
ma w zbiorze liczb rzeczywistych dokładnie:
Odpowiedzi:
| A. dwa rozwiązania: x=3, x=4 | B. dwa rozwiązania: x=3, x=-4 |
| C. dwa rozwiązania: x=3, x=0 | D. jedno rozwiązanie: x=3 |
| Zadanie 14. (1 pkt) (Numer zadania: pp-11962) | [ ⇒ Rozwiąż ] |
Podpunkt 14.1 (1 pkt)
Dana jest nierówność kwadratowa (-2x+12)(x-k)\lessdot 0
z niewiadomą x i parametrem k\in\mathbb{R}.
Rozwiązaniem tej nierówności jest przedział (-3,6).
Liczba k jest równa:
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 15. (1 pkt) (Numer zadania: pp-11966) | [ ⇒ Rozwiąż ] |
Podpunkt 15.1 (1 pkt)
Wyznacz najmniejsze i największe rozwiązanie równania
\frac{(2-x)(-2x-3)}{(5x-2)(3-2x)}=0.
Odpowiedzi:
| x_{min} | = | (wpisz dwie liczby całkowite) | |
| x_{max} | = | (wpisz dwie liczby całkowite) | |
| Zadanie 16. (1 pkt) (Numer zadania: pp-11967) | [ ⇒ Rozwiąż ] |
Podpunkt 16.1 (1 pkt)
Dana jest nierówność
3-\frac{x}{2}\geqslant \frac{x}{3}+5.
Najmniejszą liczbą całkowitą, która nie spełnia tej nierówności jest:
Odpowiedź:
x=
(wpisz liczbę całkowitą)
| Zadanie 17. (1 pkt) (Numer zadania: pp-11984) | [ ⇒ Rozwiąż ] |
Podpunkt 17.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności
11-\frac{3}{2}x\lessdot \frac{2}{3}-x jest
przedział postaci:
Odpowiedzi:
| A. \langle a, +\infty) | B. (-\infty, a\rangle |
| C. (-\infty, a) | D. (a, +\infty) |
Podpunkt 17.2 (0.8 pkt)
Liczba a jest równa:
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 18. (1 pkt) (Numer zadania: pp-11985) | [ ⇒ Rozwiąż ] |
Podpunkt 18.1 (1 pkt)
Równanie \frac{x-7}{(x-3)(7-x)}=0
ma w zbiorze liczb rzeczywistych dokładnie:
Odpowiedzi:
| A. dwa rozwiązania | B. trzy rozwiązania |
| C. zero rozwiązań | D. jedno rozwiązanie |
| Zadanie 19. (1 pkt) (Numer zadania: pp-12006) | [ ⇒ Rozwiąż ] |
Podpunkt 19.1 (1 pkt)
Liczba wszystkich całkowitych dodatnich rozwiązań nierówności
\frac{3x-68}{12}\lessdot \frac{1}{3} jest równa:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 20. (1 pkt) (Numer zadania: pp-12029) | [ ⇒ Rozwiąż ] |
Podpunkt 20.1 (1 pkt)
Iloczyn wszystkich rozwiązań równania 2(x-3)(x^2+9)=0 jest równy:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 21. (1 pkt) (Numer zadania: pp-12030) | [ ⇒ Rozwiąż ] |
Podpunkt 21.1 (0.2 pkt)
Zbiorem rozwiązań nierówności
\frac{\frac{151}{8}-5x}{2}\lessdot 3\left(\frac{27}{16}-\frac{1}{2}x\right)+7x-\frac{77}{8} jest
przedział postaci:
Odpowiedzi:
| A. (-\infty, a] | B. (-\infty, a) |
| C. (a, +\infty) | D. [a,+\infty) |
Podpunkt 21.2 (0.8 pkt)
Podaj liczbę a.
Odpowiedź:
| a= | |
| Zadanie 22. (1 pkt) (Numer zadania: pp-12057) | [ ⇒ Rozwiąż ] |
Podpunkt 22.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności
\frac{16-x}{2}-16x\geqslant 1 jest przedział postaci:
Odpowiedzi:
| A. (-\infty,a) | B. (-\infty,a] |
| C. [a,+\infty) | D. (a,+\infty) |
Podpunkt 22.2 (0.8 pkt)
Podaj liczbe a.
Odpowiedź:
| a= | |
| Zadanie 23. (1 pkt) (Numer zadania: pp-12085) | [ ⇒ Rozwiąż ] |
Podpunkt 23.1 (1 pkt)
Wskaż rysunek, na którym przedstawiony jest zbiór wszystkich liczb rzeczywistych
x, spełniających alternatywę nierówności
0 > 7-3x lub
7-3x\leqslant 5x-3:
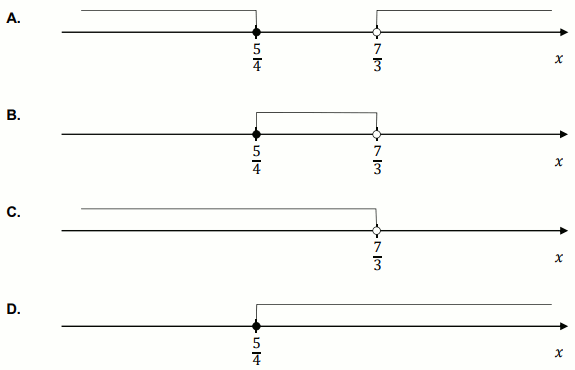
Odpowiedzi:
| A. C | B. A |
| C. D | D. B |
| Zadanie 24. (1 pkt) (Numer zadania: pp-12086) | [ ⇒ Rozwiąż ] |
Podpunkt 24.1 (1 pkt)
Wyznacz rozwiązanie równania x\sqrt{3}+6=6x-3:
Odpowiedź:
| x= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 25. (1 pkt) (Numer zadania: pp-12087) | [ ⇒ Rozwiąż ] |
Podpunkt 25.1 (1 pkt)
Podaj najmniejsze i największe rozwiązanie równania \frac{x^2-25}{x^2-5x}=0.
Odpowiedzi:
| x_{min} | = |
(wpisz liczbę całkowitą) |
| x_{max} | = |
(wpisz liczbę całkowitą) |
| Zadanie 26. (1 pkt) (Numer zadania: pp-12111) | [ ⇒ Rozwiąż ] |
Podpunkt 26.1 (1 pkt)
Liczba 8 jest rozwiązaniem równania:
Odpowiedzi:
| A. \frac{x+8}{x^2-64}=0 | B. x^2(x-8)+2x(x-8)=0 |
| C. \frac{x+1}{x+8}=0 | D. \frac{x+8}{x}=1 |
| Zadanie 27. (1 pkt) (Numer zadania: pp-12112) | [ ⇒ Rozwiąż ] |
Podpunkt 27.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności 5-\frac{2+6x}{4}\geqslant -2x+1
jest zbiór postaci:
Odpowiedzi:
| A. [a, +\infty) | B. (-\infty, a]\cup[b, +\infty) |
| C. (-\infty, a) | D. (-\infty, a] |
Podpunkt 27.2 (0.8 pkt)
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
| x_{min}= | |
| Zadanie 28. (1 pkt) (Numer zadania: pp-12185) | [ ⇒ Rozwiąż ] |
Podpunkt 28.1 (1 pkt)
Iloczyn wszystkich rozwiązań równania
4(x-3)(x^2-16)=0 jest równy:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 29. (1 pkt) (Numer zadania: pp-12186) | [ ⇒ Rozwiąż ] |
Podpunkt 29.1 (1 pkt)
Rozwiązanie nierówności
\frac{27-5x}{2}\lessdot 3\left(\frac{5}{2}-\frac{1}{2}x\right)+7x-21
zapisz w postaci przedziału.
Podaj najmniejszy koniec liczbowy tego przedziału.
Odpowiedź:
| min= | |
| Zadanie 30. (1 pkt) (Numer zadania: pp-12187) | [ ⇒ Rozwiąż ] |
Podpunkt 30.1 (1 pkt)
Podaj najmniejsze rozwiązanie równania
\frac{x^2-4x}{x^2-4x}=0:
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
| Zadanie 31. (1 pkt) (Numer zadania: pp-12188) | [ ⇒ Rozwiąż ] |
Podpunkt 31.1 (1 pkt)
Podaj sumę i iloczyn wszystkich rozwiązań równania
x(x-3)(x-4)=0:
Odpowiedzi:
| suma | = |
(wpisz liczbę całkowitą) |
| iloczyn | = |
(wpisz liczbę całkowitą) |
| Zadanie 32. (1 pkt) (Numer zadania: pp-12189) | [ ⇒ Rozwiąż ] |
Podpunkt 32.1 (1 pkt)
Liczba rozwiązań równania x(x-3)=(x-3)^2
jest równa:
Odpowiedzi:
| A. 3 | B. 0 |
| C. 2 | D. 1 |
| Zadanie 33. (1 pkt) (Numer zadania: pp-12190) | [ ⇒ Rozwiąż ] |
Podpunkt 33.1 (1 pkt)
Rozwiązaniem równania \frac{x+3}{x+4}=3 jest
liczba:
Odpowiedź:
| x= | |
| Zadanie 34. (1 pkt) (Numer zadania: pp-12191) | [ ⇒ Rozwiąż ] |
Podpunkt 34.1 (1 pkt)
Linę o długości 160 metrów rozcięto na trzy części, których
długości pozostają w stosunku 3:4:5. Z tego wynika, że
najdłuższa z tych części ma długość:
Odpowiedź:
| d\ [m]= | |
| Zadanie 35. (1 pkt) (Numer zadania: pp-12198) | [ ⇒ Rozwiąż ] |
Podpunkt 35.1 (1 pkt)
Równania (x^2+7x+12)(x^2-25)=0
nie spełnia liczba:
Odpowiedzi:
| A. -2 | B. -5 |
| C. -4 | D. 5 |
| Zadanie 36. (1 pkt) (Numer zadania: pp-12199) | [ ⇒ Rozwiąż ] |
Podpunkt 36.1 (1 pkt)
Nierówność (x+1)(x+4)^2(x-4)(x-1)>0
spełnia liczba:
Odpowiedzi:
| A. -11 | B. 1 |
| C. 3 | D. 5 |
| Zadanie 37. (1 pkt) (Numer zadania: pp-12345) | [ ⇒ Rozwiąż ] |
Podpunkt 37.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności
\frac{-2(-3-x)}{8}\leqslant 1 jest
przedział postaci:
Odpowiedzi:
| A. (a, +\infty) | B. (-\infty, a) |
| C. [a, +\infty) | D. (-\infty, a] |
Podpunkt 37.2 (0.8 pkt)
Liczba a jest równa:
Odpowiedź:
| a= | |
| Zadanie 38. (1 pkt) (Numer zadania: pp-12346) | [ ⇒ Rozwiąż ] |
Podpunkt 38.1 (0.5 pkt)
Równanie \frac{x(x-6)(-2-x)}{2x+4}=0
w zbiorze liczb rzeczywistych ma k rozwiązań.
Podaj liczbę k:
Odpowiedź:
k=
(wpisz liczbę całkowitą)
Podpunkt 38.2 (0.5 pkt)
Podaj najmniejsze i największe rozwiązanie tego równania:
Odpowiedzi:
| min | = |
(wpisz liczbę całkowitą) |
| max | = |
(wpisz liczbę całkowitą) |
| Zadanie 39. (1 pkt) (Numer zadania: pp-12386) | [ ⇒ Rozwiąż ] |
Podpunkt 39.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności 5-2(1+9x)\geqslant 2x-17
jest przedział postaci:
Odpowiedzi:
| T/N : (-\infty, a] | T/N : [a, +\infty) |
Podpunkt 39.2 (0.8 pkt)
Podaj liczbę a.
Odpowiedź:
| a= | |
| Zadanie 40. (1 pkt) (Numer zadania: pp-12387) | [ ⇒ Rozwiąż ] |
Podpunkt 40.1 (1 pkt)
Podaj najmniejsze i największe rozwiązanie równania 2x(x+3)(x^2-9)=0:
Odpowiedzi:
| min | = |
(wpisz liczbę całkowitą) |
| max | = |
(wpisz liczbę całkowitą) |
| Zadanie 41. (1 pkt) (Numer zadania: pp-12406) | [ ⇒ Rozwiąż ] |
Podpunkt 41.1 (1 pkt)
Dana jest nierówność -2-\frac{-3-2x}{2}\geqslant 3x.
Największą liczbą całkowitą, która spełnia tę nierówność, jest:
Odpowiedź:
x_{max,\in\mathbb{Z}}=
(wpisz liczbę całkowitą)
| Zadanie 42. (1 pkt) (Numer zadania: pp-12407) | [ ⇒ Rozwiąż ] |
Podpunkt 42.1 (1 pkt)
Dane jest równanie 4(x+3)^2(x^2+9)=0.
Podaj liczbę rozwiązań tego równania:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 43. (1 pkt) (Numer zadania: pp-12426) | [ ⇒ Rozwiąż ] |
Podpunkt 43.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności 3-x\leqslant \frac{5x-2}{2}
jest przedział:
Odpowiedzi:
| A. [a, b] | B. [a, +\infty) |
| C. (a,b) | D. (-\infty,a) |
| E. (a, +\infty) | F. (-\infty, a] |
Podpunkt 43.2 (0.8 pkt)
Podaj najmniejszy koniec liczbowy tego przedziału.
Odpowiedź:
| x_{min}= | |
| Zadanie 44. (1 pkt) (Numer zadania: pp-12427) | [ ⇒ Rozwiąż ] |
Podpunkt 44.1 (1 pkt)
Suma wszystkich rozwiązań równania
(-2x-3)(-2+5x)(-2-x)=0 jest równa:
Odpowiedź:
| suma= | |
| Zadanie 45. (1 pkt) (Numer zadania: pp-12445) | [ ⇒ Rozwiąż ] |
Podpunkt 45.1 (1 pkt)
Dane jest równanie 5x(x^2+2)(x^2-4x+7)=0.
Podaj liczbę rozwiązań tego równania.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 46. (1 pkt) (Numer zadania: pp-12468) | [ ⇒ Rozwiąż ] |
Podpunkt 46.1 (1 pkt)
Suma wszystkich rozwiązań równania
6(x^2-4)(x+m)(x+5)=0 jest równa 0.
Oznacza to, że liczba m jest równa:
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 47. (1 pkt) (Numer zadania: pp-12469) | [ ⇒ Rozwiąż ] |
Podpunkt 47.1 (1 pkt)
Wyznacz rozwiązanie równania \frac{x-6}{3x-25}=\frac{2}{5}.
Odpowiedź:
| x= | |