Układy równań
Zadania z matur CKE dla liceum ogólnokształcącego - poziom podstawowy
Uczeń:
- rozwiązuje układy równań liniowych z dwiema niewiadomymi, podaje interpretację geometryczną układów oznaczonych, nieoznaczonych i sprzecznych;
- stosuje układy równań do rozwiązywania zadań tekstowych;
- rozwiązuje metodą podstawiania układy równań, z których jedno jest liniowe, a drugie kwadratowe, postaci \begin{cases}ax+by=e\\x^2+y^2+cx+dy=f\end{cases} lub \begin{cases}ax+by=e\\y=ax^2+bx+c\end{cases};
| Zadanie 1. (2 pkt) (Numer zadania: pp-21043) | [ ⇒ Rozwiąż ] |
Podpunkt 1.1 (2 pkt)
Dany jest prostokąt o bokach długości a i b,
gdzie a>b. Obwód tego prostokąta jest równy
58. Jeden z boków tego prostokąta jest o
7 krótszy od drugiego.
Oceń, które z podanych układów równań opisują zależności pomiędzy bokami tego prostokąta.
Odpowiedzi:
| T/N : \begin{cases}2ab=58\\a-b=7\end{cases} | T/N : \begin{cases}2(a+b)=58\\b=a-7\end{cases} |
| T/N : \begin{cases}2a+2b=58\\b=7a\end{cases} | T/N : \begin{cases}2a+2b=58\\a-b=7\end{cases} |
| Zadanie 2. (3 pkt) (Numer zadania: pp-21092) | [ ⇒ Rozwiąż ] |
Podpunkt 2.1 (1 pkt)
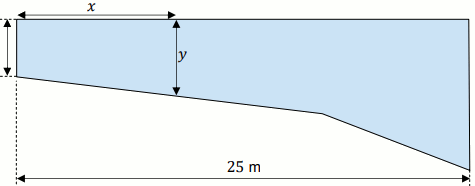
Basen ma długość 25\ m. W najpłytszym miejscu jego głębokość jest równa
1\ m. Przekrój podłużny tego basenu przedstawiono poglądowo
na rysunku. Głębokość y basenu zmienia się wraz z odległością
x od brzegu w sposób opisany funkcją:
y=\left{\begin{cases}ax+b;\ 0\leqslant x\leqslant 15\ m\\0,18x-0,9;\ 15\ m\leqslant x\leqslant 25\ m\end{cases}.
Odległość x jest mierzona od płytszego brzegu w poziomie na powierzchni wody (zobacz
rysunek). Wielkości x i y są wyrażone w metrach.
Największa głębokość basenu jest równa:
Odpowiedź:
| g\ [m]= | |
Podpunkt 2.2 (2 pkt)
Oblicz wartość współczynnika a i wartość współczynnika b.
Odpowiedzi:
| a | = | (wpisz dwie liczby całkowite) | |
| b | = | (wpisz dwie liczby całkowite) | |
| Zadanie 3. (2 pkt) (Numer zadania: pp-21198) | [ ⇒ Rozwiąż ] |
Podpunkt 3.1 (2 pkt)
W maju 2024 roku założono dwa sady: posadzono w nich łącznie 2720 drzew.
Po roku stwierdzono, że uschło 90\% drzew w pierwszym sadzie i
85\% drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych
nie dosadzano. Liczba drzew, które pozostały w drugim sadzie, stanowiła
250\% liczby drzew, które pozostały w pierwszym sadzie.
Oblicz, ile drzew posadzono w pierwszym sadzie w maju 2024 roku.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 4. (2 pkt) (Numer zadania: pp-21211) | [ ⇒ Rozwiąż ] |
Podpunkt 4.1 (2 pkt)
Właściciel restauracji kupił 80 kilogramów pomidorów:
x kg pomidorów malinowych w cenie 13
złotych za kilogram oraz y kg pomidorów cherry w cenie
22.91 złotych za kilogram. Za pomidory zapłacił łącznie
1277.84 złotych.
Oblicz, ile kilogramów pomidorów malinowych kupił właściciel restauracji.
Odpowiedź:
malinowe\ [kg]=
(wpisz liczbę całkowitą)