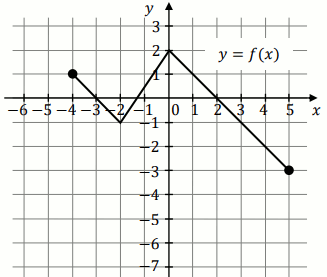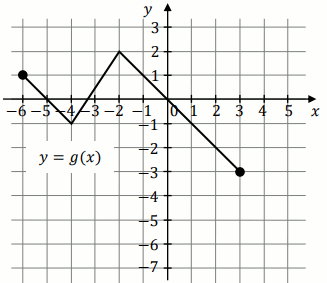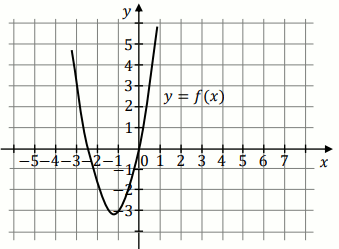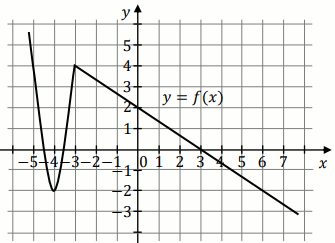Funkcje
Zadania z matur CKE dla liceum ogólnokształcącego - poziom podstawowy
Uczeń:
- określa funkcje jako jednoznaczne przyporządkowanie za pomocą opisu słownego, tabeli, wykresu, wzoru (także różnymi wzorami na różnych przedziałach);
- oblicza wartość funkcji zadanej wzorem algebraicznym;
- odczytuje i interpretuje wartości funkcji określonych za pomocą tabel, wykresów, wzorów itp., również w sytuacjach wielokrotnego użycia tego samego źródła informacji lub kilku źródeł jednocześnie;
- odczytuje z wykresu funkcji: dziedzinę, zbiór wartości, miejsca zerowe, przedziały monotoniczności, przedziały, w których funkcja przyjmuje wartości większe (nie mniejsze) lub mniejsze (nie większe) od danej liczby, największe i najmniejsze wartości funkcji (o ile istnieją) w danym przedziale domkniętym oraz argumenty, dla których wartości największe i najmniejsze są przez funkcję przyjmowane;
- interpretuje współczynniki występujące we wzorze funkcji liniowej;
- wyznacza wzór funkcji liniowej na podstawie informacji o jej wykresie lub o jej własnościach;
- szkicuje wykres funkcji kwadratowej zadanej wzorem;
- interpretuje współczynniki występujące we wzorze funkcji kwadratowej w postaci ogólnej, kanonicznej i iloczynowej (jeśli istnieje);
- wyznacza wzór funkcji kwadratowej na podstawie informacji o tej funkcji lub o jej wykresie;
- wyznacza największą i najmniejszą wartość funkcji kwadratowej w przedziale domkniętym;
- wykorzystuje własności funkcji liniowej i kwadratowej do interpretacji zagadnień geometrycznych, fizycznych itp., także osadzonych w kontekście praktycznym;
- na podstawie wykresu funkcji y=f(x) szkicuje wykresy funkcji y=f(x-a), y=f(x)+b, y=f(-x), y=-f(x);
- posługuje się funkcją f(x)=\frac{a}{x}, w tym jej wykresem, do opisu i interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi, również w zastosowaniach praktycznych;
- posługuje się funkcjami wykładniczą i logarytmiczną, w tym ich wykresami, do opisu i interpretacji zagadnień związanych z zastosowaniami praktycznymi.
| Zadanie 1. (1 pkt) (Numer zadania: pp-11765) | [ ⇒ Rozwiąż ] |
Podpunkt 1.1 (1 pkt)
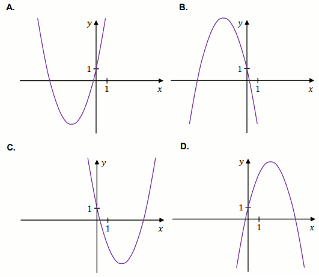
Wykres funkcji liniowej określonej wzorem f(x)=ax+b,
przechodzi przez pierwszą, drugą i trzecią ćwiartkę układu współrzędnych.
Wówczas liczby a i b spełniają warunki:
Odpowiedzi:
| A. a\lessdot 0 \wedge b \lessdot 0 | B. a > 0 \wedge b \lessdot 0 |
| C. a > 0 \wedge b > 0 | D. a\lessdot 0 \wedge b > 0 |
| Zadanie 2. (1 pkt) (Numer zadania: pp-11766) | [ ⇒ Rozwiąż ] |
Podpunkt 2.1 (1 pkt)
Jednym z miejsc zerowych funkcji kwadratowej f jest liczba
8. Pierwsza współrzędna wierzchołka paraboli, będącej
wykresem tej funkcji jest równa 5.
Drugim miejscem zerowym funkcji f jest liczba:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 3. (1 pkt) (Numer zadania: pp-11787) | [ ⇒ Rozwiąż ] |
Podpunkt 3.1 (1 pkt)
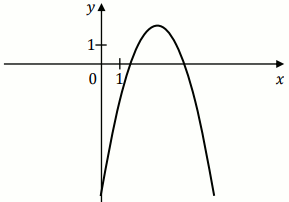
Funkcja kwadratowa f jest określona wzorem
f(x)=ax^2+bx+1, gdzie a
oraz b są pewnymi liczbami rzeczywistymi, takimi, że
a\lessdot 0 i b > 0.
Fragment wykresu funkcji f przedstawiono na rysunku:
Odpowiedzi:
| A. C | B. D |
| C. A | D. B |
| Zadanie 4. (1 pkt) (Numer zadania: pp-11812) | [ ⇒ Rozwiąż ] |
Podpunkt 4.1 (1 pkt)
Miejscem zerowym funkcji liniowej f(x)=ax+b jest liczba 2.
Wykres tej funkcji zawiera punkt o współrzędnych (-1,-5).
Podaj liczby a i b.
Odpowiedzi:
| a | = | (wpisz dwie liczby całkowite) | |
| b | = | (wpisz dwie liczby całkowite) | |
| Zadanie 5. (1 pkt) (Numer zadania: pp-11810) | [ ⇒ Rozwiąż ] |
Podpunkt 5.1 (1 pkt)
Funkcja f jest określona dla każdej liczby rzeczywistej
x wzorem f(x)=\frac{3x-k}{x^2+1}
gdzie k jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek
f(1)=2.
Wyznacz współczynnik k występujący we wzorze tej funkcji.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 6. (1 pkt) (Numer zadania: pp-11813) | [ ⇒ Rozwiąż ] |
Podpunkt 6.1 (1 pkt)
Funkcja kwadratowa f jest określona wzorem
f(x)=(x-2)^2-81.
Jednym z miejsc zerowych tej funkcji jest liczba x_1=-7.
Drugim miejscem zerowym funkcji f jest liczba:
Odpowiedź:
x_2=
(wpisz liczbę całkowitą)
| Zadanie 7. (1 pkt) (Numer zadania: pp-11835) | [ ⇒ Rozwiąż ] |
Podpunkt 7.1 (1 pkt)
Funkcja liniowa f jest określona wzorem
f(x)=-\frac{1}{16}x+\frac{1}{8}.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : miejscem zerowym funkcji f jest liczba 2 | T/N : punkt przecięcia wykresu funkcji f z osią Oy ma współrzędne\left(0,\frac{1}{8}\right) |
| Zadanie 8. (1 pkt) (Numer zadania: pp-11839) | [ ⇒ Rozwiąż ] |
Podpunkt 8.1 (1 pkt)
Proces stygnięcia naparu z ziół w otoczeniu o stałej temperaturze 12^{\circ}
opisuje funkcja wykładnicza T(x)=80\cdot 2^{-\frac{1}{5}x}+12, gdzie
T(x) to temperatura naparu wyrażona w stopniach Celsjusza po
x minutach liczonych od momentu x=0, w którym zioła
zalano wrzątkiem.
Temperatura naparu po 20 minutach od momentu zalania ziół wrzątkiem jest równa:
Odpowiedź:
| T\ [^{\circ}C]= | |
| Zadanie 9. (1 pkt) (Numer zadania: pp-11857) | [ ⇒ Rozwiąż ] |
Podpunkt 9.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji f:
Iloczyn f(-2)\cdot f(-7)\cdot f(4) jest równy:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) (Numer zadania: pp-11858) | [ ⇒ Rozwiąż ] |
Podpunkt 10.1 (1 pkt)
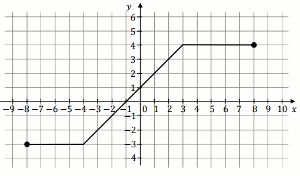
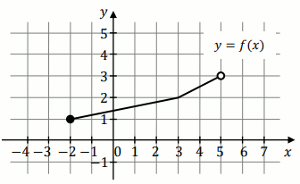
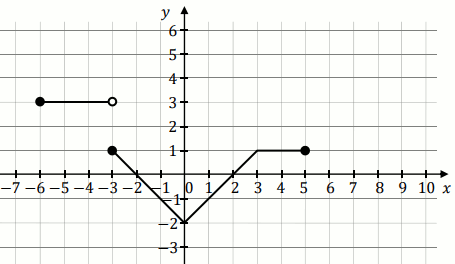
Na rysunku 1. przedstawiono wykres funkcji f określonej na zbiorze
[-4,5]:
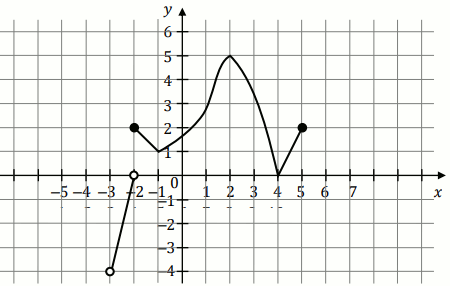
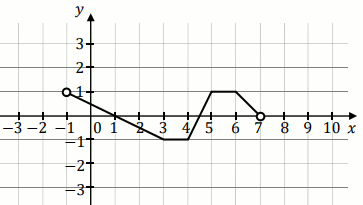
Funkcję g określono za pomocą funkcji f.
Wykres funkcji g przedstawiono na rysunku 2:
Wynika stąd, że:
Odpowiedzi:
| A. g(x)=f(x-2) | B. g(x)=f(-x)+2 |
| C. g(x)=f(x+2) | D. g(x)=f(x)+2 |
| E. g(x)=f(x)-2 | F. g(x)=f(-x)-2 |
| Zadanie 11. (1 pkt) (Numer zadania: pp-11859) | [ ⇒ Rozwiąż ] |
Podpunkt 11.1 (1 pkt)
Miejscem zerowym funkcji liniowej f określonej wzorem
f(x)=-\frac{1}{2}(x+2)-5 jest liczba:
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 12. (1 pkt) (Numer zadania: pp-11864) | [ ⇒ Rozwiąż ] |
Podpunkt 12.1 (1 pkt)
Wykresem funkcji kwadratowej f(x)=3x^2+bx+c jest parabola o wierzchołku
w punkcie W=(-2,-5). Wzór tej funkcji w postaci kanonicznej to:
Odpowiedzi:
| A. f(x)=3(x+5)^2-2 | B. f(x)=3(x-2)^2-5 |
| C. f(x)=3(x+2)^2+5 | D. f(x)=3(x+2)^2-5 |
| E. f(x)=3(x-5)^2-2 | F. f(x)=3(x-2)^2+5 |
| Zadanie 13. (1 pkt) (Numer zadania: pp-11884) | [ ⇒ Rozwiąż ] |
Podpunkt 13.1 (1 pkt)
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f
określonej wzorem f(x)=2x^2+5x:
Osią symetrii wykresu funkcji g określonej wzorem g(x)=f(x-2) jest prosta o równaniu x=a.
Podaj liczbę a.
Odpowiedź:
| a= | |
| Zadanie 14. (1 pkt) (Numer zadania: pp-11890) | [ ⇒ Rozwiąż ] |
Podpunkt 14.1 (1 pkt)
Dana jest funkcja kwadratowa f określona
wzorem f(x)=2x^2-2x. Funkcja kwadratowa
g jest określona wzorem g(x)=2x^2+2x.
Wykres funkcji g jest:
Odpowiedzi:
| A. symetryczny do wykresu funkcji f względem osi Ox | B. symetryczny do wykresu funkcji f względem osi Oy |
| C. symetryczny do wykresu funkcji f względem punktu O=(0,0) | D. przesunięty względem wykresu funkcji f o -4 jednostek w kierunku przeciwnym do zwrotu osi Ox |
| Zadanie 15. (1 pkt) (Numer zadania: pp-11886) | [ ⇒ Rozwiąż ] |
Podpunkt 15.1 (1 pkt)
Funkcja f jest określona wzorem f(x)=\frac{3}{x}-3
dla każdej liczby rzeczywistej x\neq 0.
Liczba f(1)-f(-1) jest równa:
Odpowiedź:
| f(x_0)-f(-x_0)= | |
| Zadanie 16. (1 pkt) (Numer zadania: pp-11887) | [ ⇒ Rozwiąż ] |
Podpunkt 16.1 (1 pkt)
Punkt M=(3, -2) należy do wykresu funkcji liniowej f
określonej wzorem f(x)=5x+b-7.
Wynika stąd, że b jest równe:
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 17. (1 pkt) (Numer zadania: pp-11889) | [ ⇒ Rozwiąż ] |
Podpunkt 17.1 (1 pkt)
Funkcja kwadratowa f określona wzorem
f(x)=-(x+4)^2+2 jest rosnąca w przedziale:
Odpowiedzi:
| A. \langle -4,+\infty\rangle | B. (-\infty, 4\rangle |
| C. \langle 4,+\infty\rangle | D. (-\infty, -4\rangle |
| Zadanie 18. (1 pkt) (Numer zadania: pp-11888) | [ ⇒ Rozwiąż ] |
Podpunkt 18.1 (1 pkt)
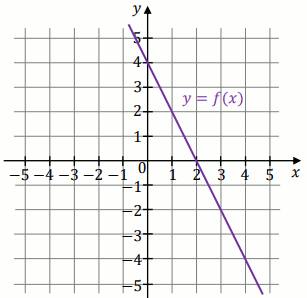
Na rysunku jest przedstawiony fragment wykresu funkcji okreslonej wzorem
y=f(x):
W przedziale (-4,6) równanie f(x)=-2:
Odpowiedzi:
| A. ma trzy rozwiązania | B. nie ma rozwiązań |
| C. ma jedno rozwiązanie | D. ma dwa rozwiązania |
| Zadanie 19. (1 pkt) (Numer zadania: pp-11914) | [ ⇒ Rozwiąż ] |
Podpunkt 19.1 (0.2 pkt)
Funkcja liniowa f określona wzorem
f(x)=(3m-5)x+22 jest rosnąca dla:
wszystkich m należących do przedziału postaci:
Odpowiedzi:
| A. [a, +\infty) | B. (-\infty, a] |
| C. (a, +\infty) | D. (-\infty, a) |
Podpunkt 19.2 (0.8 pkt)
Podaj liczbę a.
Odpowiedź:
| a= | |
| Zadanie 20. (1 pkt) (Numer zadania: pp-11915) | [ ⇒ Rozwiąż ] |
Podpunkt 20.1 (1 pkt)
Funkcja kwadratowa f określona wzorem
f(x)=x^2+bx+c osiąga dla x=1
wartość najmniejszą równą -10.
Podaj liczby b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 21. (1 pkt) (Numer zadania: pp-11916) | [ ⇒ Rozwiąż ] |
Podpunkt 21.1 (1 pkt)
Dana jest funkcja kwadratowa f określona wzorem
f(x)=-2(x-3)(x+6).
Funkcja f jest rosnąca w zbiorze:
Odpowiedzi:
| A. \left(-\infty, 4\right\rangle | B. \left\langle -6,+\infty\right) |
| C. \left(-\infty, -\frac{3}{2}\right\rangle | D. \left\langle 3,+\infty\right) |
| E. \left(-\infty, 3\right\rangle | F. \left(-\infty, -\frac{5}{4}\right\rangle |
| Zadanie 22. (1 pkt) (Numer zadania: pp-11917) | [ ⇒ Rozwiąż ] |
Podpunkt 22.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji f określonej na zbiorze
\langle -2, 5):
Funkcja g jest określona za pomocą funkcji f następująco: g(x)=f(x+1). Wykres funkcji g można otrzymać poprzez odpowiednie przesunięcie wykresu funkcji f.
Dziedziną funkcji g jest zbiór przedział liczbowy o końcach
a i b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 23. (1 pkt) (Numer zadania: pp-11920) | [ ⇒ Rozwiąż ] |
Podpunkt 23.1 (1 pkt)
W ciągu dwóch godzin trzy jednakowe maszyny produkują razem 2160
guzików.
Ile guzików wyprodukuje pięć takich maszyn w ciągu jednej godziny? Przyjmij, że maszyny pracują z taką samą, stałą wydajnością.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 24. (1 pkt) (Numer zadania: pp-11961) | [ ⇒ Rozwiąż ] |
Podpunkt 24.1 (1 pkt)
Funkcja f jest określona wzorem
f(x)=-\log{x}, dla wszystkich liczb rzeczywistych
dodatnich x.
Wartość funkcji f dla argumentu x_0=\sqrt[8]{10^{7}} jest równa:
Odpowiedź:
| f(x_0)= | |
| Zadanie 25. (1 pkt) (Numer zadania: pp-11963) | [ ⇒ Rozwiąż ] |
Podpunkt 25.1 (0.4 pkt)
Dana jest funkcja kwadratowa f(x)=ax^2+bx+c, gdzie
a, b i c
są liczbami rzeczywistymi takimi, że a\neq 0
oraz c\lessdot 0. Funkcja f
nie ma miejsc zerowych.
Wykres funkcji f leży w całości:
Odpowiedzi:
| A. nad osią Ox | B. pod osią Ox |
Podpunkt 25.2 (0.6 pkt)
Powyższa odpowiedź jest poprawna, ponieważ:
Odpowiedzi:
| A. a\lessdot 0 i b^2-4ac\lessdot 0 | B. a > 0 i b^2-4ac\lessdot 0 |
| C. a\lessdot 0 i b^2-4ac=0 | D. a\lessdot 0 i b\lessdot 0 |
| Zadanie 26. (1 pkt) (Numer zadania: pp-11965) | [ ⇒ Rozwiąż ] |
Podpunkt 26.1 (1 pkt)
Dany jest wielomian W(x) określony wzorem
W(x)=x^3-5x^2+3x-15 dla każdej liczby rzeczywistej.
x.
Wielomian W(x) można zapisać w postaci
W(x)=(x+a)(x^2+b).
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 27. (1 pkt) (Numer zadania: pp-11986) | [ ⇒ Rozwiąż ] |
Podpunkt 27.1 (1 pkt)
Dany jest wielomian W(x)=3x^3+6x^2-45x.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : liczba -5 jest pierwiastkiem wielomianu W(x) | T/N : wielomian W(x) ma dokładnie dwa pierwiastki |
| Zadanie 28. (1 pkt) (Numer zadania: pp-11989) | [ ⇒ Rozwiąż ] |
Podpunkt 28.1 (0.2 pkt)
Funkcja liniowa f jest określona wzorem
f(x)=(-7k+4)x+k-4, gdzie
k\in\mathbb{R}.
Funkcja f jest malejąca dla każdej liczby k należącej do przedziału postaci:
Odpowiedzi:
| A. \left(a,+\infty\right) | B. \left(-\infty,a\right) |
Podpunkt 28.2 (0.8 pkt)
Liczba a jest równa:
Odpowiedź:
| a= | |
| Zadanie 29. (1 pkt) (Numer zadania: pp-11990) | [ ⇒ Rozwiąż ] |
Podpunkt 29.1 (1 pkt)
Funkcje liniowe f oraz g,
określone wzorami f(x)=-2x-5 oraz
g(x)=ax-6, mają to samo miejsce zerowe.
Współczynnik a we wzorze funkcji g jest równy:
Odpowiedź:
| a= | |
| Zadanie 30. (1 pkt) (Numer zadania: pp-12010) | [ ⇒ Rozwiąż ] |
Podpunkt 30.1 (1 pkt)
Wielomian W(x)=ax^3+bx^2+cx+d jest iloczynem wielomianów
F(x)=(3-5x)^2 oraz G(x)=-5x+3.
Suma a+b+c+d współczynników wielomianu W(x) jest równa:
Odpowiedź:
a+b+c+d=
(wpisz liczbę całkowitą)
| Zadanie 31. (1 pkt) (Numer zadania: pp-12011) | [ ⇒ Rozwiąż ] |
Podpunkt 31.1 (1 pkt)
Funkcja y=f(x) jest określona za pomocą tabeli:
------------------------------ | x | -2 | -1 | 0 | 1 | 2 | ------------------------------ | y | -3 | 0 | 2 | 0 | -3 | ------------------------------
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : wykres funkcji f jest symetryczny względem osi Oy | T/N : funkcja f ma dwa miejsca zerowe |
| Zadanie 32. (1 pkt) (Numer zadania: pp-12012) | [ ⇒ Rozwiąż ] |
Podpunkt 32.1 (1 pkt)
Liczba 2 jest miejscem zerowym funkcji liniowej
f(x)=(6-m)x+4.
Liczba m jest równa:
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 33. (1 pkt) (Numer zadania: pp-12031) | [ ⇒ Rozwiąż ] |
Podpunkt 33.1 (1 pkt)
Funkcja liniowa f(x)=(a-7)x+4 osiąga wartość najmniejszą
równą 4.
Wtedy a jest równe:
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 34. (1 pkt) (Numer zadania: pp-12032) | [ ⇒ Rozwiąż ] |
Podpunkt 34.1 (1 pkt)
Na wykresie przedstawiono wykres funkcji f:
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : funkcja f dla argumentu -2 przyjmuje wartość 2 | T/N : funkcja f ma dwa miejsca zerowe |
| Zadanie 35. (1 pkt) (Numer zadania: pp-12033) | [ ⇒ Rozwiąż ] |
Podpunkt 35.1 (1 pkt)
Funkcja f jest określona wzorem
f(x)=\frac{2x+2}{2x^2+3} dla każdej
liczby rzeczywistej x.
Wartość funkcji f dla argumentu 1 jest równa:
Odpowiedź:
| f(1)= | |
| Zadanie 36. (1 pkt) (Numer zadania: pp-12058) | [ ⇒ Rozwiąż ] |
Podpunkt 36.1 (1 pkt)
Na poniższym rysunku przedstawiono wykres funkcji f określonej w zbiorze
[-6,5].
Funkcja g jest określona wzorem
g(x)=f(x)-2.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : funkcja g nie ma miejsc zerowych | T/N : funkcje f i g mają taki sam zbiór wartości |
| T/N : f(-2)+g(-2)=-2 |
| Zadanie 37. (1 pkt) (Numer zadania: pp-12061) | [ ⇒ Rozwiąż ] |
Podpunkt 37.1 (1 pkt)
Funkcja f jest określona wzorem
f(x)=\frac{(x-5)^2}{2x-12}
dla każdej liczby rzeczywistej x\neq 1.
Wtedy dla argumentu x_0=\sqrt{3}+4 wartość funkcji f jest równa:
Odpowiedź:
| f(x_0)= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 38. (1 pkt) (Numer zadania: pp-12062) | [ ⇒ Rozwiąż ] |
Podpunkt 38.1 (1 pkt)
Do wykresu funkcji f określonej dla każdej liczby rzeczywistej
x wzorem f(x)=3^x-2 należy
punkt o współrzędnych (2,y), gdy:
Odpowiedź:
y=
(wpisz liczbę całkowitą)
| Zadanie 39. (1 pkt) (Numer zadania: pp-12063) | [ ⇒ Rozwiąż ] |
Podpunkt 39.1 (0.2 pkt)
Funkcja kwadratowa f określona wzorem
f(x)=-5(x-3)(x-5) jest malejąca
w przedziale o maksymalnej długości postaci:
Odpowiedzi:
| A. \left\langle a,+\infty) | B. \left(-\infty,a\rangle |
Podpunkt 39.2 (0.8 pkt)
Podaj liczbę a.
Odpowiedź:
| a= | |
| Zadanie 40. (1 pkt) (Numer zadania: pp-12088) | [ ⇒ Rozwiąż ] |
Podpunkt 40.1 (1 pkt)
Na poniższym rysunku przedstawiono wykres funkcji f określonej w zbiorze
(-1,7).
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : funkcja f ma dwa miejsca zerowe | T/N : zbiorem wartości funkcji f jest przedział [-1,1) |
| T/N : funkcja f jest monotoniczna w przedziale (-1,4) |
| Zadanie 41. (1 pkt) (Numer zadania: pp-12089) | [ ⇒ Rozwiąż ] |
Podpunkt 41.1 (1 pkt)
Wykresem funkcji kwadratowej f określonej wzorem
f(x)=(x-4)(x-2) jest parabola
o wierzchołku W=(p,q).
Współrzędne wierzchołka W spełniają warunki:
Odpowiedzi:
| A. p \lessdot 0 i q \lessdot 0 | B. p > 0 i q > 0 |
| C. p > 0 i q \lessdot 0 | D. p \lessdot 0 i q > 0 |
| Zadanie 42. (1 pkt) (Numer zadania: pp-12113) | [ ⇒ Rozwiąż ] |
Podpunkt 42.1 (1 pkt)
Funkcja liniowa f jest określona wzorem
f(x)=-5x+3. Wykres funkcji f
przesunięto wzdłuż osi Ox o 2
jednostki w lewo (tzn. przeciwnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji
g(a)=ax+b.
Podaj współczynniki a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 43. (1 pkt) (Numer zadania: pp-12114) | [ ⇒ Rozwiąż ] |
Podpunkt 43.1 (1 pkt)
Funkcja f określona jest wzorem f(x)=ax-7
dla każdej liczby rzeczywistej x. Miejscem zerowym funkcji
f jest liczba \frac{9}{4}.
Wtedy a jest równe:
Odpowiedź:
| a= | |
| Zadanie 44. (1 pkt) (Numer zadania: pp-12116) | [ ⇒ Rozwiąż ] |
Podpunkt 44.1 (1 pkt)
Funkcja kwadratowa f jest określona wzorem
f(x)=-5(x-3)(x-5). Wierzchołek paraboli,
która jest wykresem funkcji f, ma współrzędną x_w równą:
Odpowiedź:
| x_w= | |
| Zadanie 45. (1.2 pkt) (Numer zadania: pp-12117) | [ ⇒ Rozwiąż ] |
Podpunkt 45.1 (0.2 pkt)
Funkcja f jest określona wzorem f(x)=-x^2+4
dla każdej liczby rzeczywistej x.
Zbiorem wartości funkcji f jest przedział postaci:
Odpowiedzi:
| A. (-\infty,a) | B. (a,+\infty) |
| C. [a,+\infty) | D. (-\infty,a] |
Podpunkt 45.2 (1 pkt)
Podaj liczbę a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 46. (1 pkt) (Numer zadania: pp-12118) | [ ⇒ Rozwiąż ] |
Podpunkt 46.1 (1 pkt)
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f:
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji f.
Odpowiedzi:
| A. y=-x^2-7x-12 | B. y=x^2-7x-12 |
| C. y=x^2-7x-12 | D. y=-x^2+0x+4 |
| E. y=-x^2+x+2 | F. y=-x^2+11x-18 |
| Zadanie 47. (1 pkt) (Numer zadania: pp-12192) | [ ⇒ Rozwiąż ] |
Podpunkt 47.1 (1 pkt)
Funkcje liniowe f i g określone
wzorami f(x)=-2x+12 i g(x)=-2x+k+3
mają wspólne miejsce zerowe. Wynika z tego, że:
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 48. (1 pkt) (Numer zadania: pp-12193) | [ ⇒ Rozwiąż ] |
Podpunkt 48.1 (0.5 pkt)
Zbiorem wartości funkcji f określonej wzorem
f(x)=-(x-8)^2+4jest zbiór postaci:
Odpowiedzi:
| A. (-\infty,a) | B. (a,+\infty) |
| C. [a,+\infty) | D. (-\infty,a] |
Podpunkt 48.2 (0.5 pkt)
Zapisz ten zbiór w postaci przedziału i podaj jego koniec liczbowy a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 49. (1 pkt) (Numer zadania: pp-12194) | [ ⇒ Rozwiąż ] |
Podpunkt 49.1 (1 pkt)
Osią symetrii wykresu funkcji kwadratowej f określonej
wzorem f(x)=-\frac{5}{6}x^2+3x-7 jest
prosta o równaniu x=a.
Podaj liczbę a.
Odpowiedź:
| a= | |
| Zadanie 50. (1 pkt) (Numer zadania: pp-12195) | [ ⇒ Rozwiąż ] |
Podpunkt 50.1 (1 pkt)
Parabola, która jest wykresem funkcji kwadratowej f(x)=ax^2+bx+c
ma ramiona skierowane ku górze, a jej wierzchołek znajduje się na osi
Ox, po
prawej stronie osi Oy.
Wówczas:
Odpowiedzi:
| A. a > 0 \wedge c \lessdot 0 | B. a \lessdot 0 \wedge c \lessdot 0 |
| C. a > 0 \wedge c > 0 | D. a \lessdot 0 \wedge c > 0 |
| Zadanie 51. (1 pkt) (Numer zadania: pp-12196) | [ ⇒ Rozwiąż ] |
Podpunkt 51.1 (1 pkt)
Punkty P=(-7,8) i O=(0,0) należą
do jednej prostej.
Wyznacz tangens kąta nachylenia tej prostej do osi Ox.
Odpowiedź:
| \tan\alpha= | |
| Zadanie 52. (1 pkt) (Numer zadania: pp-12197) | [ ⇒ Rozwiąż ] |
Podpunkt 52.1 (1 pkt)
Funkcja f jest określona wzorem f(x)=\left(\frac{1}{2}\right)^x
dla wszystkich liczb rzeczywistych x.
Funkcja f dla argumentu x_0=-3 przyjmuje wartość:
Odpowiedź:
| f\left(x_0\right)= | |
| Zadanie 53. (1 pkt) (Numer zadania: pp-12200) | [ ⇒ Rozwiąż ] |
Podpunkt 53.1 (1 pkt)
Wielkości x i y są odwrotnie
proporcjonalne:
\begin{tabular}{|c|c|c|}
\hline
x & 18 & a \\ \hline
y & 24 & 6 \\ \hline
\end{tabular}
Wyznacz a,
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 54. (1 pkt) (Numer zadania: pp-12201) | [ ⇒ Rozwiąż ] |
Podpunkt 54.1 (1 pkt)
Boki trójkąta ABC są zawarte w prostych o równaniach
y=-\frac{5}{6}x+7 i y=-2x+7 oraz osi
Ox układu współrzędnych.
Wyznacz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle ABC}= | |
| Zadanie 55. (1 pkt) (Numer zadania: pp-12203) | [ ⇒ Rozwiąż ] |
Podpunkt 55.1 (1 pkt)
Punkt P=(-3, 7) należy do wykresu funkcji liniowej
f określonej wzorem f(x)=(2m-35)x+5.
Zatem:
Odpowiedź:
| m= | |
| Zadanie 56. (1 pkt) (Numer zadania: pp-12204) | [ ⇒ Rozwiąż ] |
Podpunkt 56.1 (1 pkt)
Wykresem funkcji kwadratowej f określonej wzorem
f(x)=-2x^2+8x-19 jest parabola o wierzchołku
w punkcie \left(2,q\right).
Liczba q jest równa:
Odpowiedź:
q=
(wpisz liczbę całkowitą)
| Zadanie 57. (1 pkt) (Numer zadania: pp-12205) | [ ⇒ Rozwiąż ] |
Podpunkt 57.1 (1 pkt)
Funkcja f każdej liczbie naturalnej przyporządkowuje resztę
z dzielenia tej liczby przez 4.
Wyznacz zbiór wartości funkcji f i podaj średnią wartość wszystkich liczb z tego zbioru.
Odpowiedź:
| \overline{x}_{ZW_f}= | |
| Zadanie 58. (1 pkt) (Numer zadania: pp-12206) | [ ⇒ Rozwiąż ] |
Podpunkt 58.1 (1 pkt)
Parabola, która jest wykresem funkcji kwadratowej f(x)=ax^2+bx+c
ma ramiona skierowane ku dołowi, a jej wierzchołek znajduje się na osi
Ox, po
prawej stronie osi Oy.
Wówczas:
Odpowiedzi:
| A. a > 0 \wedge b > 0 | B. a \lessdot 0 \wedge b > 0 |
| C. a \lessdot 0 \wedge b \lessdot 0 | D. a > 0 \wedge b \lessdot 0 |
| Zadanie 59. (1 pkt) (Numer zadania: pp-12207) | [ ⇒ Rozwiąż ] |
Podpunkt 59.1 (1 pkt)
Proste o równaniach y=(-4m+4)x oraz
y=\frac{3}{7}x+1 są prostopadłe.
Wówczas:
Odpowiedź:
| m= | |
| Zadanie 60. (1 pkt) (Numer zadania: pp-12208) | [ ⇒ Rozwiąż ] |
Podpunkt 60.1 (0.5 pkt)
Funkcja kwadratowa f jest określona wzorem
f(x)=a(x-1)(x-5). Wierzchołkiem
paraboli, która jest wykresem funkcji f jest punkt
W=(3,4).
Oznacza to, że współczynnik a jest równy:
Odpowiedź:
| a= | |
Podpunkt 60.2 (0.5 pkt)
Największa wartość funkcji f w przedziale
[1,6] jest równa:
Odpowiedź:
f_{MAX}(x)=
(wpisz liczbę całkowitą)
| Zadanie 61. (1 pkt) (Numer zadania: pp-12209) | [ ⇒ Rozwiąż ] |
Podpunkt 61.1 (1 pkt)
Do wykresu funkcji liniowej f określonej wzorem
f(x)=ax+b należą punkty A=(0,1)
B=(1,-1).
Wynika z tego, że:
Odpowiedzi:
| A. a\cdot b > 0 | B. a\in(-1,0) |
| C. a+b=0 | D. a\cdot b\lessdot 0 |
| Zadanie 62. (1 pkt) (Numer zadania: pp-12210) | [ ⇒ Rozwiąż ] |
Podpunkt 62.1 (1 pkt)
Funkcja f jest określona wzorem
f(x)=9^{-x}+4.
Liczba f\left(\frac{1}{2}\right) jest równa:
Odpowiedź:
| f\left(\frac{1}{2}\right)= | |
| Zadanie 63. (1 pkt) (Numer zadania: pp-12211) | [ ⇒ Rozwiąż ] |
Podpunkt 63.1 (1 pkt)
Punkt A=\left(-\frac{14}{3},2\right)
należy do wykresu funkcji określonej wzorem f(x)=3x+b.
Wyznacz liczbę b.
Odpowiedź:
| b= | |
| Zadanie 64. (1 pkt) (Numer zadania: pp-12212) | [ ⇒ Rozwiąż ] |
Podpunkt 64.1 (1 pkt)
Funkcja kwadratowa określona wzorem f(x)=x^2+bx+c ma dwa
dodatnie miejsca zerowe, a jej wykres przecina oś Oy poniżej
punktu O=(0,0).
Wówczas:
Odpowiedzi:
| A. b\lessdot 0 \wedge c > 0 | B. b\lessdot 0 \wedge c \lessdot 0 |
| C. b > 0 \wedge c > 0 | D. b > 0 \wedge c \lessdot 0 |
| Zadanie 65. (1 pkt) (Numer zadania: pp-12213) | [ ⇒ Rozwiąż ] |
Podpunkt 65.1 (1 pkt)
Miejscami zerowymi funkcji kwadratowej f określonej wzorem
f(x)=1-(6-x)^2 są liczby x_1
i x_2.
Wówczas:
Odpowiedzi:
| x_1+x_2 | = |
(wpisz liczbę całkowitą) |
| x_1\cdot x_2 | = |
(wpisz liczbę całkowitą) |
| Zadanie 66. (1 pkt) (Numer zadania: pp-12214) | [ ⇒ Rozwiąż ] |
Podpunkt 66.1 (1 pkt)
We wzorze funkcji kwadratowej f(x)=ax^2+bx+c współczynnik
a jest ujemny, a parabola, która jest wykresem tej funkcji ma
wierzchołek w punkcie W=(-5, 4).
Oceń, które z podanych liczb należą do zbioru wartości tej funkcji:
Odpowiedzi:
| T/N : 7 | T/N : 2 |
| T/N : 5 | T/N : 9 |
| Zadanie 67. (1 pkt) (Numer zadania: pp-12215) | [ ⇒ Rozwiąż ] |
Podpunkt 67.1 (1 pkt)
Punkt A=(a, 6) należy do prostej określonej równaniem
y=\frac{3}{4}x+\frac{51}{4}.
Wynika z tego, że:
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 68. (1 pkt) (Numer zadania: pp-12216) | [ ⇒ Rozwiąż ] |
Podpunkt 68.1 (1 pkt)
Funkcja liniowa f jest określona wzorem
f(x)=(2m+5)x+11, gdzie m
to pewna liczba rzeczywista, ma miejsce zerowe równe \frac{3}{4}.
Wynika z tego, że:
Odpowiedź:
| m= | |
| Zadanie 69. (1 pkt) (Numer zadania: pp-12217) | [ ⇒ Rozwiąż ] |
Podpunkt 69.1 (1 pkt)
Funkcja f jest określona dla każdej liczby rzeczywistej
x wzorem f(x)=(m\sqrt{7}+21)x+2.
Podaj najmniejsze m całkowite, dla którego funkcja ta jest rosnąca.
Odpowiedź:
m_{\in\mathbb{Z}, min}=
(wpisz liczbę całkowitą)
| Zadanie 70. (1 pkt) (Numer zadania: pp-12219) | [ ⇒ Rozwiąż ] |
Podpunkt 70.1 (1 pkt)
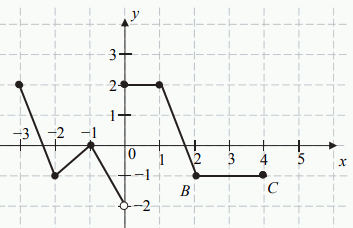
Rysunek przedstawia wykres funkcji f zbudowany z 6 odcinków, przy czym
punkty B=(2, -1) i C=(4,-1) należą do wykresu funkcji.
Równanie f(x)=2 ma:
Odpowiedzi:
| A. więcej niż trzy rozwiązania | B. jedno rozwiązanie |
| C. dwa rozwiązania | D. trzy rozwiązania |
| Zadanie 71. (1 pkt) (Numer zadania: pp-12220) | [ ⇒ Rozwiąż ] |
Podpunkt 71.1 (1 pkt)
Miejscem zerowym funkcji liniowej f określonej wzorem
f(x)=2(x-3)-\sqrt{5} jest liczba:
Odpowiedź:
| x_0= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 72. (1 pkt) (Numer zadania: pp-12221) | [ ⇒ Rozwiąż ] |
Podpunkt 72.1 (0.5 pkt)
Wierzchołkiem paraboli, która jest wykresem funkcji kwadratowej f jest punkt
W=(-1,6), a punkt O=(0,0) należy do tej paraboli.
Wyznacz niezerowe miejsce zerowe funkcji f.
Odpowiedź:
x_{\neq 0}=
(wpisz liczbę całkowitą)
Podpunkt 72.2 (0.25 pkt)
Zbiorem wartości funkcji f jest przedział:
Odpowiedzi:
| A. [6, +\infty) | B. [-6, +\infty) |
| C. (-\infty, 6] | D. [-1, +\infty) |
Podpunkt 72.3 (0.25 pkt)
Osią symetrii tej paraboli jest prosta o równaniu:
Odpowiedzi:
| A. x=6 | B. y=-1 |
| C. y=6 | D. x=-1 |
| Zadanie 73. (1 pkt) (Numer zadania: pp-12222) | [ ⇒ Rozwiąż ] |
Podpunkt 73.1 (1 pkt)
Dane są funkcje f(x)=3^x-7 oraz g(x)=f(-x)
określone dla rzeczywistych x. Punkt wspólny wykresów funkcji
f i g ma współrzędne (x_0,y_0).
Podaj liczby x_0 i y_0.
Odpowiedzi:
| x_0 | = |
(wpisz liczbę całkowitą) |
| y_0 | = |
(wpisz liczbę całkowitą) |
| Zadanie 74. (1 pkt) (Numer zadania: pp-12223) | [ ⇒ Rozwiąż ] |
Podpunkt 74.1 (1 pkt)
Punkt (1,3-5\sqrt{3}) należy do wykresu funkcji
f(x)=-5\sqrt{3}x+b.
Wtedy współczynnik b jest równy:
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 75. (1 pkt) (Numer zadania: pp-12348) | [ ⇒ Rozwiąż ] |
Podpunkt 75.1 (0.5 pkt)
Funkcja y=f(x) jest określona za pomocą tabeli:
-------------------------------------------------- | x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | -------------------------------------------------- | y | -7 | 4 | -7 | 6 | -5 | -4 | -2 | 1 | 0 | --------------------------------------------------
Wskaż największą wartość tej funkcji:
Odpowiedź:
max=
(wpisz liczbę całkowitą)
Podpunkt 75.2 (0.5 pkt)
Wskaż miejsce zerowe tej funkcji:
Odpowiedź:
x_0=
(wpisz liczbę całkowitą)
| Zadanie 76. (1 pkt) (Numer zadania: pp-12349) | [ ⇒ Rozwiąż ] |
Podpunkt 76.1 (1 pkt)
Funkcja liniowa f jest określona wzorem
f(x)=\frac{\sqrt{2}}{7}x+2. W kartezjańskim układzie
współrzędnych (x, y) wykres funkcji
y=f(x) jest prostą nachyloną do osi Ox
pod kątem ostrym \alpha.
Wyznacz sinus kąta \alpha:
Odpowiedź:
| \sin\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 77. (1 pkt) (Numer zadania: pp-12370) | [ ⇒ Rozwiąż ] |
Podpunkt 77.1 (1 pkt)
Miejscem zerowym funkcji liniowej f określonej wzorem f(x)=ax+b jest liczba
2, a punkt przecięcia wykresu funkcji f
z osią Ox kartezjańskiego układu współrzędnych
(x, y) ma współrzędne (0,4)
(zobacz rysunek).
Oceń poprawność poniższych zdań:
Odpowiedzi:
| T/N : a\cdot b > 0 | T/N : prosta odcina na osiach układu trójkąt o polu równym 8 |
| Zadanie 78. (1 pkt) (Numer zadania: pp-12371) | [ ⇒ Rozwiąż ] |
Podpunkt 78.1 (1 pkt)
Funkcja logarytmiczna f jest określona wzorem
f(x)=\log_{2}{x} dla każdej dodatniej liczby
rzeczywistej x.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : funkcja f przyjmuje tylko wartości dodatnie | T/N : funkcja f ma miejsce zerowe |
| Zadanie 79. (1 pkt) (Numer zadania: pp-12389) | [ ⇒ Rozwiąż ] |
Podpunkt 79.1 (1 pkt)
Funkcja liniowa f jest określona wzorem
f(x)=(3-5m)x-3.
Funkcja ta nie ma miejsca zerowego dla m równego:
Odpowiedź:
| m= | |
| Zadanie 80. (1 pkt) (Numer zadania: pp-12408) | [ ⇒ Rozwiąż ] |
Podpunkt 80.1 (1 pkt)
Funkcja liniowa f jest określona wzorem
f(x)=\frac{1}{2}x-k+10, gdzie
k jest liczbą rzeczywistą. Miejsce zerowe funkcji
f jest liczbą większą od 2.
Liczba k należy do przedziału (a, +\infty). Podaj liczbę a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 81. (1 pkt) (Numer zadania: pp-12409) | [ ⇒ Rozwiąż ] |
Podpunkt 81.1 (1 pkt)
Funkcja liniowa f jest określona wzorem f(x)=5x.
W kartezjańskim układzie współrzędnych (x,y) wykres funkcji
f przesunięto o wektor o współrzędnych \vec{u}=[-5,3],
w wyniku czego otrzymano wykres funkcji liniowej g(x)=ax+b.
Podaj liczby a i b.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 82. (1 pkt) (Numer zadania: pp-12428) | [ ⇒ Rozwiąż ] |
Podpunkt 82.1 (1 pkt)
Miejscem zerowym funkcji liniowej g określonej wzorem g(x)=ax+b jest liczba -2.
Dla argumentu 0 funkcja g przyjmuje
wartość -9.
Podaj liczby a i b.
Odpowiedzi:
| a | = | (wpisz dwie liczby całkowite) | |
| b | = | (wpisz dwie liczby całkowite) | |