Trygonometria
Zadania z matur CKE dla liceum ogólnokształcącego - poziom podstawowy
Uczeń:
- wykorzystuje definicje funkcji: sinus, cosinus i tangens dla kątów od 0^{\circ} do 180^{\circ}, w szczególności wyznacza wartości funkcji trygonometrycznych dla kątów 30^{\circ}, 45^{\circ} i 60^{\circ};
- znajduje przybliżone wartości funkcji trygonometrycznych, korzystając z tablic lub kalkulatora;
- znajduje za pomocą tablic lub kalkulatora przybliżoną wartość kąta, jeśli dana jest wartość funkcji trygonometrycznej;
- korzysta z wzorów \sin^2\alpha+\cos^2\alpha=1, \tan\alpha=\frac{\sin\alpha}{\cos\alpha};
- stosuje twierdzenia sinusów i cosinusów oraz wzór na pole trójkąta P=\frac{1}{2}\cdot a\cdot b\cdot\sin\alpha;
- oblicza kąty trójkąta i długości jego boków przy odpowiednich danych (rozwiązuje trójkąty).
| Zadanie 1. (2 pkt) (Numer zadania: pp-21063) | [ ⇒ Rozwiąż ] |
Podpunkt 1.1 (1 pkt)
Dane są dwa kąty o miarach \alpha oraz \beta,
spełniające warunki: \alpha\in\left(0^{\circ},180^{\circ}\right) i
\tan\alpha=-\frac{2}{3} oraz \beta\in\left(0^{\circ},180^{\circ}\right)
i \cos\beta=\frac{1}{\sqrt{10}}.
Na rysunkach A–F w kartezjańskim układzie współrzędnych (x, y) zaznaczono różne kąty – w tym kąt o mierze \alpha oraz kąt o mierze \beta. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią Ox, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: A lub B, lub C, lub D, lub E, lub F.
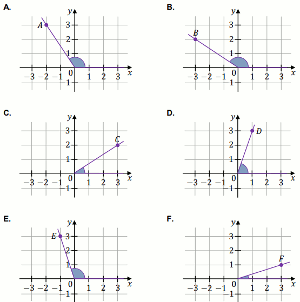
Kąt \alpha zaznaczony jest na rysunku:
Odpowiedzi:
| A. E | B. B |
| C. D | D. A |
| E. C | F. F |
Podpunkt 1.2 (1 pkt)
Kąt \beta zaznaczony jest na rysunku:
Odpowiedzi:
| A. E | B. A |
| C. B | D. D |
| E. C | F. F |
| Zadanie 2. (2 pkt) (Numer zadania: pp-21070) | [ ⇒ Rozwiąż ] |
Podpunkt 2.1 (2 pkt)
Kąt \alpha jest ostry i \tan\alpha=6.
Oblicz wartość wyrażenia \sin^2\alpha.
Odpowiedź:
| \sin^2\alpha= | |
| Zadanie 3. (2 pkt) (Numer zadania: pp-21103) | [ ⇒ Rozwiąż ] |
Podpunkt 3.1 (2 pkt)
W kartezjańskim układzie współrzędnych (x,y) zaznaczono
kąt skierowany w standardowym położeniu o mierze \alpha
taki, że \tan\alpha=-\frac{7}{2} oraz
90^{\circ}\lessdot \alpha\lessdot 180^{\circ}.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : \sin\alpha\lessdot \cos\alpha | T/N : \sin\alpha=-\frac{2}{7}\cos\alpha |
| T/N : \sin\alpha > \cos\alpha | T/N : \sin\alpha=\frac{2}{7}\cos\alpha |
| Zadanie 4. (2 pkt) (Numer zadania: pp-21119) | [ ⇒ Rozwiąż ] |
Podpunkt 4.1 (2 pkt)
Kąt \alpha jest ostry i
\sin\alpha+\cos\alpha=1.
Oblicz wartość wyrażenia \sin\alpha\cos\alpha.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 5. (2 pkt) (Numer zadania: pp-21159) | [ ⇒ Rozwiąż ] |
Podpunkt 5.1 (2 pkt)
Kąt \alpha jest ostry i spełnia warunek
\frac{6\sin{\alpha}-7\cos{\alpha}}{\cos{\alpha}}=7.
Oblicz tangens kąta \alpha.
Odpowiedź:
| \tan{\alpha}= | |
| Zadanie 6. (2 pkt) (Numer zadania: pp-21160) | [ ⇒ Rozwiąż ] |
Podpunkt 6.1 (2 pkt)
Kąt \alpha jest ostry i
\sin\alpha+\cos\alpha=\frac{6\sqrt{2}}{7}.
Oblicz wartośc wyrażenia \tan\alpha+\frac{1}{\tan\alpha}.
Odpowiedź:
| \tan{\alpha}+\frac{1}{\tan\alpha}= | |
| Zadanie 7. (2 pkt) (Numer zadania: pp-21161) | [ ⇒ Rozwiąż ] |
Podpunkt 7.1 (2 pkt)
Kąt \alpha jest ostry i spełniona jest równość
\sin\alpha+\cos\alpha=\frac{\sqrt{7}}{7}.
Oblicz wartośc wyrażenia w=(\cos\alpha-\sin\alpha)^2.
Odpowiedź:
| w= | |
| Zadanie 8. (2 pkt) (Numer zadania: pp-21162) | [ ⇒ Rozwiąż ] |
Podpunkt 8.1 (2 pkt)
Kąt \alpha jest ostry i spełnia równość
\tan\alpha+\frac{1}{\tan\alpha}=4.
Oblicz wartość wyrażenia \sin\alpha\cdot\cos\alpha.
Odpowiedź:
| \sin\alpha\cdot \cos\alpha= | |