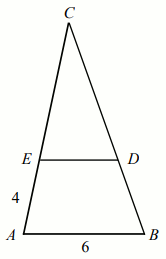Planimetria z CKE
Zadania z matur CKE dla liceum ogólnokształcącego - poziom podstawowy
Uczeń:
wyznacza promienie i średnice okręgów, długości cięciw okręgów oraz odcinków stycznych, w tym z wykorzystaniem twierdzenia Pitagorasa;
rozpoznaje trójkąty ostrokątne, prostokątne i rozwartokątne przy danych długościach boków (m.in. stosuje twierdzenie odwrotne do twierdzenia Pitagorasa i twierdzenie cosinusów); stosuje twierdzenie: w trójkącie naprzeciw większego kąta wewnętrznego leży dłuższy bok;
rozpoznaje wielokąty foremne i korzysta z ich podstawowych własności;
korzysta z własności kątów i przekątnych w prostokątach, równoległobokach, rombach i trapezach;
stosuje własności kątów wpisanych i środkowych;
stosuje wzory na pole wycinka koła i długość łuku okręgu;
stosuje twierdzenia: Talesa, odwrotne do twierdzenia Talesa, o dwusiecznej kąta oraz o kącie między styczną a cięciwą;
korzysta z cech podobieństwa trójkątów;
wykorzystuje zależności między obwodami oraz między polami figur podobnych;
wskazuje podstawowe punkty szczególne w trójkącie: środek okręgu wpisanego w trójkąt, środek okręgu opisanego na trójkącie, ortocentrum, środek ciężkości oraz korzysta z ich własności;
stosuje funkcje trygonometryczne do wyznaczania długości odcinków w figurach płaskich oraz obliczania pól figur;
przeprowadza dowody geometryczne.
Zadanie 1. (1 pkt) (Numer zadania: pp-11772)
[ ⇒ Rozwiąż ]
Podpunkt 1.1 (1 pkt)
W rombie o boku długości
2\sqrt{3} kąt rozwarty ma miarę
150^{\circ} .
Iloczyn długości przekątnych tego rombu jest równy:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 2. (1 pkt) (Numer zadania: pp-11770)
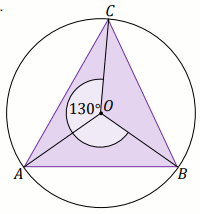
[ ⇒ Rozwiąż ]
Podpunkt 2.1 (1 pkt)
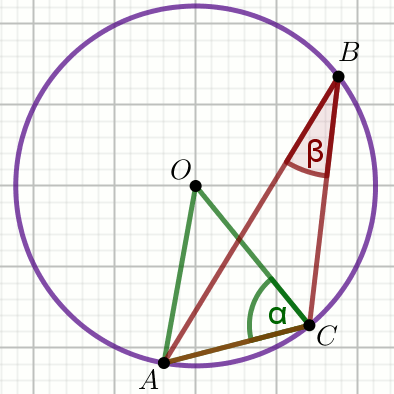
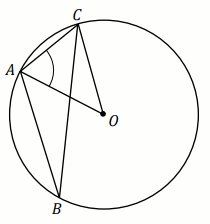
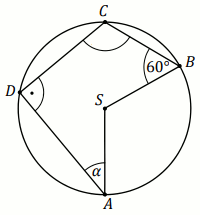
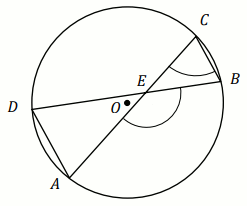
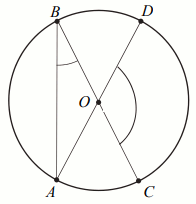
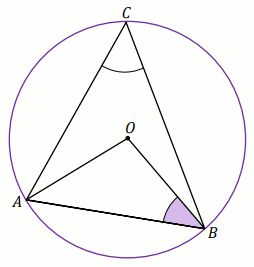
Punkty
A ,
B i
C
należą do okręgu o środku w punkcie
O , a kąt
\alpha ma miarę
48^{\circ} :
Miara stopniowa kąta \beta jest równa:
Odpowiedź:
\beta \ [^{\circ}]=
(wpisz liczbę całkowitą)
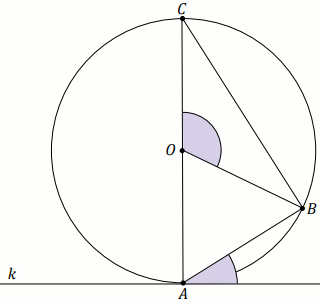
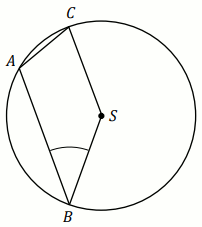
Zadanie 3. (1 pkt) (Numer zadania: pp-11792)
[ ⇒ Rozwiąż ]
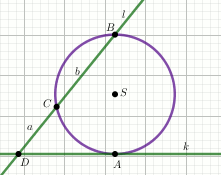
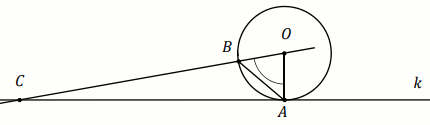
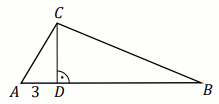
Podpunkt 3.1 (1 pkt)
Odcinek
AB jest średnicą okręgu o środku
S .
Prosta
k jest styczna do tego okręgu w punkcie
A .
Prosta
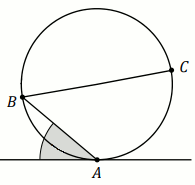
l przecina ten okrąg w punktach
B i
C . Proste
k i
l
przecinają się w punkcie
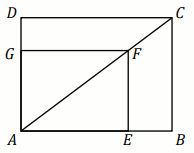
D , przy czym
a=3
i
b=4 (zobacz rysunek).
Odległość punktu A od prostej l jest równa:
Odpowiedź:
Zadanie 4. (1 pkt) (Numer zadania: pp-11794)
[ ⇒ Rozwiąż ]
Podpunkt 4.1 (1 pkt)
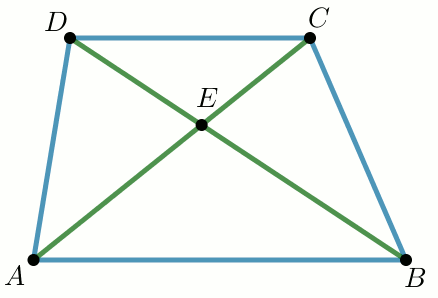
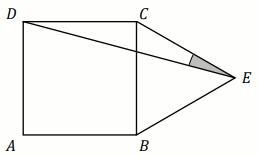
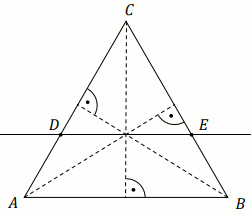
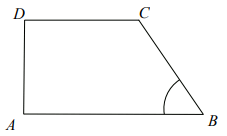
W trapezie
ABCD o podstawach
AB i
CD przekątne przecinają się w punkcie
E
(zobacz rysunek).
Oceń prawdziwość poniższych stwierdzeń:
Odpowiedzi:
T/N : P_{\triangle ACD}=P_{\triangle BCD}
T/N : \triangle ABE \sim \triangle DEC
Zadanie 5. (1 pkt) (Numer zadania: pp-11793)
[ ⇒ Rozwiąż ]
Podpunkt 5.1 (1 pkt)
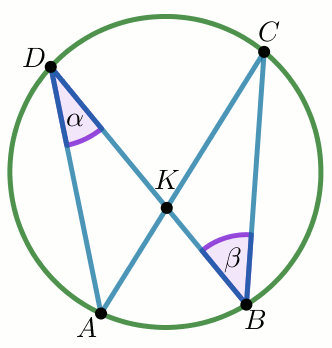
Na łukach
AB i
CD okręgu są oparte kąty wpisane
ADB i
DBC , takie, że
\alpha=14^{\circ} i
\beta=24^{\circ} (zobacz rysunek).
Cięciwy
AC i
BD przecinają się w punkcie
K .
Miara stopniowa kąta DKC jest równa:
Odpowiedź:
|\sphericalangle DKC|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 6. (1 pkt) (Numer zadania: pp-11795)
[ ⇒ Rozwiąż ]
Podpunkt 6.1 (0.5 pkt)
Pole trójkąta równobocznego
T_1 jest równe
\frac{(0.5)^2\sqrt{3}}{4} .
Pole trójkąta równobocznego
T_2 jest równe
\frac{(1.0)^2\sqrt{3}}{4} .
Trójkąt T_2 jest podobny do trójkąta T_1 w skali:
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 6.2 (0.5 pkt)
Oceń, które z podanych zdań poprawnie uzasadniają powyższą odpowiedź:
Odpowiedzi:
T/N : ponieważ pole trójkąta T_2 jest 4 razy większe od pola trójkąta T_1
T/N : ponieważ bok trójkąta T_2 jest o 0.5 dłuższy od boku trójkąta T_1
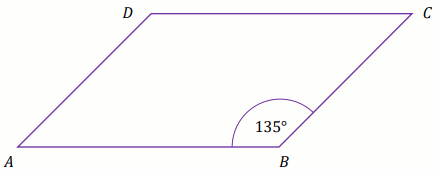
Zadanie 7. (1 pkt) (Numer zadania: pp-11796)
[ ⇒ Rozwiąż ]
Podpunkt 7.1 (1 pkt)
Pole równoległoboku
ABCD jest równe
1848 .
Bok
AD tego równoległoboku ma długość
42 , a kąt
ABC równoległoboku ma miarę
135^{\circ} (zobacz rysunek).
Długość boku AB jest równa:
Odpowiedź:
Zadanie 8. (1 pkt) (Numer zadania: pp-11818)
[ ⇒ Rozwiąż ]
Podpunkt 8.1 (1 pkt)
Trapez
T_1 , o polu równym
28 i obwodzie
34 , jest podobny do trapezu
T_2 .
Pole powierzchni trapezu
T_2 jest równe
7 .
Obwód trapezu T_2 jest równy:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 9. (1 pkt) (Numer zadania: pp-11819)
[ ⇒ Rozwiąż ]
Podpunkt 9.1 (1 pkt)
Koło ma promień równy
2 .
Obwód wycinka tego koła o kącie środkowym
30^{\circ} jest równy
a+b\cdot \pi .
Podaj liczby a i b .
Odpowiedzi:
Zadanie 10. (1 pkt) (Numer zadania: pp-11820)
[ ⇒ Rozwiąż ]
Podpunkt 10.1 (1 pkt)
W okręgu
\mathcal{O} kąt środkowy
\beta
oraz kąt wpisany
\alpha są oparte na tym samym łuku.
Kąt
\beta ma miarę o
26^{\circ} większą od kąta
\alpha .
Miara stopniowa kąta \beta jest równa:
Odpowiedź:
\beta\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 11. (1 pkt) (Numer zadania: pp-11821)
[ ⇒ Rozwiąż ]
Podpunkt 11.1 (1 pkt)
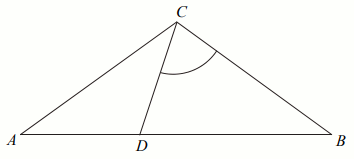
W trójkącie
ABC długość boku
AC jest równa
9 , a długość boku
BC jest równa
3 . Dwusieczna kąta
ACB przecina bok
AB w punkcie
D .
Stosunek |AD|:|DB| jest równy:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 12. (1 pkt) (Numer zadania: pp-11845)
[ ⇒ Rozwiąż ]
Podpunkt 12.1 (1 pkt)
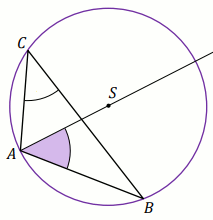
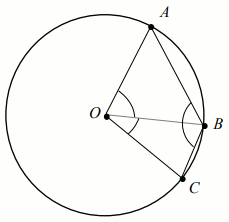
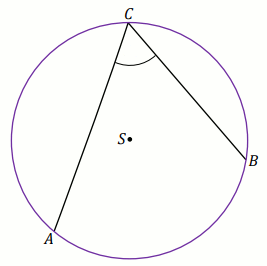
Punkty
A ,
B oraz
C
leżą na okręgu o środku w punkcie
O . Prosta
k
jest styczna do tego okręgu w punkcie
A i tworzy z cięciwą
AB kąt o mierze
28^{\circ} . Ponadto odcinek
AC jest średnicą tego okręgu (zobacz rysunek).
Miara stopniowa kąta rozwartego BOC jest równa:
Odpowiedź:
|\sphericalangle BOC|=
(wpisz liczbę całkowitą)
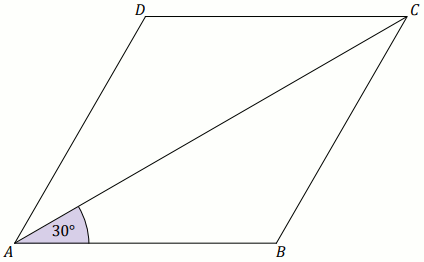
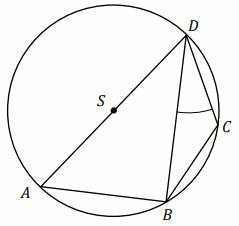
Zadanie 13. (1 pkt) (Numer zadania: pp-11846)
[ ⇒ Rozwiąż ]
Podpunkt 13.1 (1 pkt)
W rombie
ABCD dłuższa przekątna
AC ma długość
6 i tworzy z bokiem
AB kąt o mierze
30^{\circ} (zobacz rysunek).
Pole rombu ABCD jest równe:
Odpowiedź:
Zadanie 14. (1 pkt) (Numer zadania: pp-11866)
[ ⇒ Rozwiąż ]
Podpunkt 14.1 (1 pkt)
Punkty
A ,
B ,
C
leżą na okręgu o środku
S . Punkt
D jest punktem
przecięcia cięciwy
AC i średnicy okręgu poprowadzonej z punktu
B . Miara kąta
BSC jest równa
104^{\circ} , a miara kąta
ADB=\gamma jest równa
30^{\circ} (zobacz rysunek).
Wtedy kąt ABD ma miarę:
Odpowiedź:
|\sphericalangle ABD|=
(wpisz liczbę całkowitą)
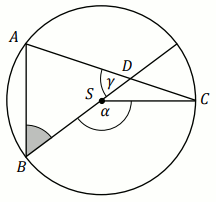
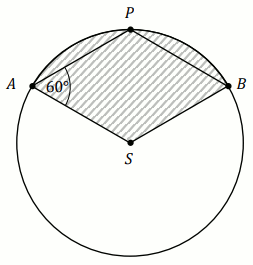
Zadanie 15. (1 pkt) (Numer zadania: pp-11874)
[ ⇒ Rozwiąż ]
Podpunkt 15.1 (1 pkt)
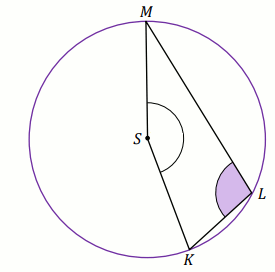
Punkty
A ,
B ,
P leżą
na okręgu o środku
S i promieniu długości
3 .
Czworokąt
ASBP jest rombem, w którym kąt ostry
PAS
ma miarę
60^{\circ} (zobacz rysunek).
Pole powierzchni zakreskowanej na rysunku figury jest równe a\cdot\pi .
Podaj liczbę a .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 16. (1 pkt) (Numer zadania: pp-11848)
[ ⇒ Rozwiąż ]
Podpunkt 16.1 (1 pkt)
Wysokość trójkąta równobocznego jest równa
2\sqrt{2} . Pole powierzchni
tego trójkąta jest równe:
Odpowiedź:
Zadanie 17. (1 pkt) (Numer zadania: pp-11871)
[ ⇒ Rozwiąż ]
Podpunkt 17.1 (1 pkt)
Boki równoległoboku mają długości
3 i
8 ,
a kąt rozwarty między tymi bokami ma miarę
120^{\circ} . Pole powierzchni
tego równoległoboku jest równe:
Odpowiedź:
Zadanie 18. (1 pkt) (Numer zadania: pp-11892)
[ ⇒ Rozwiąż ]
Podpunkt 18.1 (1 pkt)
Na trójkącie ostrokątnym
ABC opisano okrąg o środku
O .
Miara kąta
ABC jest równa
79^{\circ} .
Miara stopniowa kąta ACO jest równa:
Odpowiedź:
|\sphericalangle ACO| \ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 19. (1 pkt) (Numer zadania: pp-11893)
[ ⇒ Rozwiąż ]
Podpunkt 19.1 (1 pkt)
Trójkąt
ABC jest prostokątny. Odcinek
AD jest
wysokością tego trójkąta poprowadzoną z wierzchołka
A na przeciwprostokątną
BC .
Wtedy:
Odpowiedzi:
A. \frac{|AD|}{|AB|}=\frac{|AC|}{|AB|}
B. \frac{|AD|}{|AB|}=\frac{|BC|}{|BD|}
C. \frac{|AD|}{|AB|}=\frac{|CD|}{|AD|}
D. \frac{|AD|}{|AB|}=\frac{|CD|}{|AC|}
Zadanie 20. (1 pkt) (Numer zadania: pp-11894)
[ ⇒ Rozwiąż ]
Podpunkt 20.1 (1 pkt)
Pole rombu o obwodzie
52 i kącie rozwartym
120^{\circ} jest równe:
Odpowiedź:
Zadanie 21. (1 pkt) (Numer zadania: pp-11896)
[ ⇒ Rozwiąż ]
Podpunkt 21.1 (1 pkt)
Na boku
BC kwadratu
ABCD (na zewnątrz) zbudowano
trójkąt równoboczny
BEC (zobacz rysunek).
Miara stopniowa kąta DCE=\alpha jest równa:
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
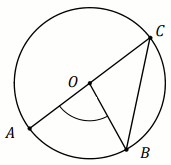
Zadanie 22. (1 pkt) (Numer zadania: pp-11923)
[ ⇒ Rozwiąż ]
Podpunkt 22.1 (1 pkt)
Wierzchołki
A ,
B ,
C
czworokąta
ABSC leżą na okręgu o środku
S .
Kąt
ABS ma miarę
74^{\circ} (zobacz rysunek),
a przekątna
BC jest dwusieczną tego kąta.
Miara stopniowa kąta ASC jest równa:
Odpowiedź:
|\sphericalangle ASC|=
(wpisz liczbę całkowitą)
Zadanie 23. (1 pkt) (Numer zadania: pp-11924)
[ ⇒ Rozwiąż ]
Podpunkt 23.1 (1 pkt)
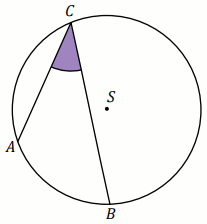
Punkty
A oraz
B leżą na okręgu o środku
S . Kąt środkowy
ASB ma miarę
144^{\circ} . Prosta
l jest styczna do
tego okręgu w punkcie
A i tworzy z cięciwą
AB
okręgu kąt o mierze
\alpha (zobacz rysunek).
Wtedy:
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 24. (1 pkt) (Numer zadania: pp-11925)
[ ⇒ Rozwiąż ]
Podpunkt 24.1 (1 pkt)
Pole prostokąta jest równe
\frac{784}{3} , a przekątne
tego prostokąta przecinają się pod kątem ostrym
\alpha , takim, że
\sin\alpha=\frac{1}{24} .
Długość przekątnej tego prostokąta jest równa:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
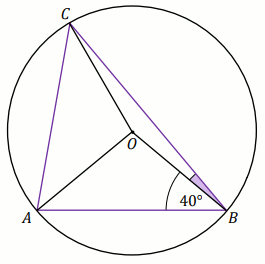
Zadanie 25. (1 pkt) (Numer zadania: pp-11953)
[ ⇒ Rozwiąż ]
Podpunkt 25.1 (1 pkt)
Punkty
A ,
B oraz
C
należą do okręgu o środku w punkcie
O . Kąt
ABO ma miarę
40^{\circ} , a kąt
OBC ma miarę
24^{\circ} (zobacz rysunek).
Miara kąta ACO jest równa:
Odpowiedź:
|\sphericalangle ACO|=
(wpisz liczbę całkowitą)
Zadanie 26. (1 pkt) (Numer zadania: pp-11954)
[ ⇒ Rozwiąż ]
Podpunkt 26.1 (1 pkt)
W trójkącie
ABC bok
AB ma długość
1,4 , a bok
BC ma długość
2,8 . Dwusieczna kąta
ABC
przecina bok
AC w punkcie
D takim,
że
|AD|=1,8 (zobacz rysunek).
Odcinek CD ma długość:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 27. (1 pkt) (Numer zadania: pp-11971)
[ ⇒ Rozwiąż ]
Podpunkt 27.1 (1 pkt)
Punkty
A ,
B ,
C
leżą na okręgu o środku
O (zobacz rysunek).
Ponadto
|\sphericalangle BOA}|=126^{\circ} .
Miara stopniowa kąta CAB jest równa:
Odpowiedź:
|\sphericalangle CAB|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 28. (1 pkt) (Numer zadania: pp-11972)
[ ⇒ Rozwiąż ]
Podpunkt 28.1 (1 pkt)
Dany jest kwadrat
ABCD o boku długości
3 . Z wierzchołka
A
zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
Pole powierzchni części wspólnej koła i kwadratu jest równe
a\cdot \pi . Podaj liczbę a .
Odpowiedź:
Zadanie 29. (1 pkt) (Numer zadania: pp-11973)
[ ⇒ Rozwiąż ]
Podpunkt 29.1 (1 pkt)
Odcinki
AC i
BD przecinają się
w punkcie
O . Ponadto
|AD|=1 ,
|OD|=|BC|=2 .
Kąty
ODA i
BCO są proste
(zobacz rysunek).
Długość odcinka OC jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 30. (1 pkt) (Numer zadania: pp-11974)
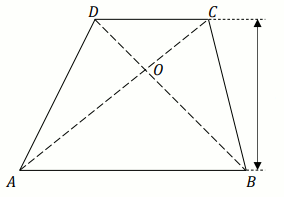
[ ⇒ Rozwiąż ]
Podpunkt 30.1 (1 pkt)
Dany jest trapez
ABCD , w którym
AB\paralel CD oraz przekątne
AC i
BD przecinają się w
punkcie
O (zobacz rysunek). Wysokość tego trapezu jest
równa
14 . Obwód trójkąta
ABO jest
równy
14 , a obwód trójkąta
CDO
jest równy
7 .
Wysokość trójkąta ABO poprowadzona z punktu
O jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 31. (1 pkt) (Numer zadania: pp-11994)
[ ⇒ Rozwiąż ]
Podpunkt 31.1 (1 pkt)
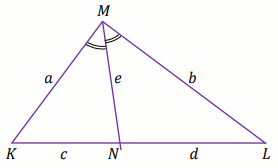
Dany jest trójkąt
KLM , w którym
|KM|=a ,
|LM|=b oraz
a\neq b . Dwusieczna kąta
KML przecina bok
KL w punkcie
N takim, że
|KN|=c ,
|NL|=d oraz
|MN|=e (zobacz rysunek).
Dla danych a=3 , b=\frac{39}{2} i
c=11 , liczba d jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 32. (1 pkt) (Numer zadania: pp-11995)
[ ⇒ Rozwiąż ]
Podpunkt 32.1 (1 pkt)
Dany jest równoległobok o bokach długości
2 i
8 oraz o kącie między nimi o mierze
120^{\circ} .
Pole powierzchni tego równoległoboku jest równe:
Odpowiedź:
Zadanie 33. (1 pkt) (Numer zadania: pp-11996)
[ ⇒ Rozwiąż ]
Podpunkt 33.1 (1 pkt)
W trójkącie
ABC , wpisanym w okrąg o środku w punkcie
S ,
kąt
ACB ma miarę
59^{\circ} (zobacz rysunek).
Miara stopniowa kąta ostrego BAS jest równa:
Odpowiedź:
|\sphericalangle BAS| \ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 34. (1 pkt) (Numer zadania: pp-12016)
[ ⇒ Rozwiąż ]
Podpunkt 34.1 (1 pkt)
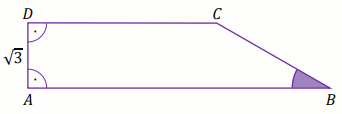
Podstawy trapezu prostokątnego
ABCD mają długości:
|AB|=11 oraz
|CD|=10 .
Wysokość
AD tego trapezu ma długość
\sqrt{3} (zobacz rysunek).
.
Miara stopniowa kąta ostrego ABC jest równa:
Odpowiedź:
|\sphericalangle ABC|=
(wpisz liczbę całkowitą)
Zadanie 35. (1 pkt) (Numer zadania: pp-12017)
[ ⇒ Rozwiąż ]
Podpunkt 35.1 (1 pkt)
Punkty
A ,
B oraz
C
leżą na okręgu o środku w punkcie
S . Długość łuku
AB ,
na którym jest oparty kąt wpisany
ACB , jest równa
\frac{1}{10} długości okręgu (zobacz rysunek).
Miara stopniowa kąta ostrego ACB jest równa:
Odpowiedź:
|\sphericalangle ACB| \ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 36. (1 pkt) (Numer zadania: pp-12036)
[ ⇒ Rozwiąż ]
Podpunkt 36.1 (1 pkt)
Trójkąt
ABC jest wpisany w okrąg o środku
O .
Miara kąta
CAO jest równa
60^{\circ}
(zobacz rysunek).
Wtedy miara stopniowa kąta ABC jest równa:
Odpowiedź:
|\sphericalangle ABC|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 37. (1 pkt) (Numer zadania: pp-12039)
[ ⇒ Rozwiąż ]
Podpunkt 37.1 (1 pkt)
W romb o boku
2\sqrt{3} i kącie
60^{\circ} wpisano okrąg.
Promień tego okręgu jest równy:
Odpowiedź:
Zadanie 38. (1 pkt) (Numer zadania: pp-12040)
[ ⇒ Rozwiąż ]
Podpunkt 38.1 (1 pkt)
Przez punkt przecięcia wysokości trójkąta równobocznego
ABC
poprowadzono prostą
DE równoległą do podstawy
AB (zobacz rysunek).
Stosunek pola trójkąta ABC do pola trójkąta
CDE jest równy a:b .
a i b .
Odpowiedzi:
Zadanie 39. (1 pkt) (Numer zadania: pp-12041)
[ ⇒ Rozwiąż ]
Podpunkt 39.1 (1 pkt)
Końcami odcinka
PR są punkty
P=(-4,-1) i
R=(4,3) .
Odległość punktu T=(-1,-2) od środka S odcinka
PR jest równa:
Odpowiedź:
|ST|=
\cdot √
(wpisz dwie liczby całkowite)
Zadanie 40. (1 pkt) (Numer zadania: pp-12046)
[ ⇒ Rozwiąż ]
Podpunkt 40.1 (1 pkt)
W trapezie równoramiennym
ABCD podstawy
AB
i
CD mają długości równe odpowiednio
a
i
b (przy czym
a > b ). Miara
kąta ostrego trapezu jest równa
30^{\circ} .
Wtedy wysokość tego trapezu jest równa m\cdot(a-b) .
m .
Odpowiedź:
Zadanie 41. (1 pkt) (Numer zadania: pp-12068)
[ ⇒ Rozwiąż ]
Podpunkt 41.1 (1 pkt)
Prosta
k jest styczna w punkcie
A
do okręgu o środku
O . Punkt
B leży na
tym okręgu i miara kąta
AOB jest równa
54^{}\circ{ . Przez punkty
O i
B poprowadzono prostą, która przecina prostą
k w punkcie
C (zobacz rysunek).
Miara kąta BAC jest równa:
Odpowiedź:
|\sphericalangle BAC|=
(wpisz liczbę całkowitą)
Zadanie 42. (1 pkt) (Numer zadania: pp-12069)
[ ⇒ Rozwiąż ]
Podpunkt 42.1 (1 pkt)
Przyprostokątna
AC trójkąta prostokątnego
ABC
ma długość
8 oraz
\tan\alpha=\frac{10}{9}
(zobacz rysunek).
Pole tego trójkąta jest równe:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 43. (1 pkt) (Numer zadania: pp-12070)
[ ⇒ Rozwiąż ]
Podpunkt 43.1 (1 pkt)
Pole pewnego trójkąta równobocznego jest równe
\frac{\sqrt{3}}{16} .
Obwód tego trójkąta jest równy:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 44. (1 pkt) (Numer zadania: pp-12071)
[ ⇒ Rozwiąż ]
Podpunkt 44.1 (1 pkt)
W trójkącie
ABC bok
BC ma długość
26 , a wysokość
CD tego trójkąta
dzieli bok
AB na odcinki o długościach
|AD|=3 i
|BD|=24 (zobacz rysunek).
Długość boku AC jest równa:
Odpowiedź:
Zadanie 45. (1 pkt) (Numer zadania: pp-12072)
[ ⇒ Rozwiąż ]
Podpunkt 45.1 (1 pkt)
Punkty
A ,
B ,
C
i
D leżą na okręgu o środku
S . Miary kątów
SBC ,
BCD ,
CDA
są równe odpowiednio:
60^{\circ} ,
127^{\circ} ,
90^{\circ} (zobacz rysunek).
Wynika z tego, że miara \alpha jest równa:
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 46. (1 pkt) (Numer zadania: pp-12074)
[ ⇒ Rozwiąż ]
Podpunkt 46.1 (1 pkt)
W każdym
n -kącie wypukłym (
n\geqslant 3 )
liczba przekątnych jest równa
\frac{n(n-3)}{2} .
Wielokątem wypukłym, w którym liczba przekątnych jest o 25
większa od liczby jego boków, jest k -kąt wypukły.
k jest równa:
Odpowiedź:
k=
(wpisz liczbę całkowitą)
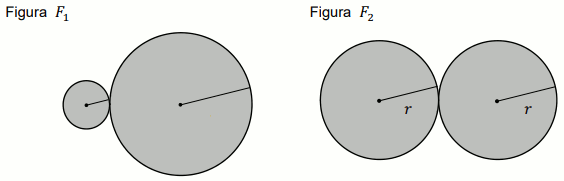
Zadanie 47. (1 pkt) (Numer zadania: pp-12075)
[ ⇒ Rozwiąż ]
Podpunkt 47.1 (1 pkt)
Pole figury
F_1 złożonej z dwóch stycznych zewnętrznie kół
o promieniach
1 i
2 jest równe
polu figury
F_2 złożonej z dwóch stycznych zewnętrznie kół o
promieniach długości
r (zobacz rysunek).
Długość promienia r jest równa:
Odpowiedź:
Zadanie 48. (1 pkt) (Numer zadania: pp-12093)
[ ⇒ Rozwiąż ]
Podpunkt 48.1 (1 pkt)
Na okręgu o środku w punkcie
O leżą punkty
A ,
B oraz
C . Odcinek
AC jest średnicą tego okręgu, a kąt środkowy
AOB ma miarę
86^{\circ} (zobacz rysunek).
Miara stopniowa kąta OBC jest równa:
Odpowiedź:
|\sphericalangle OBC|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 49. (1 pkt) (Numer zadania: pp-12094)
[ ⇒ Rozwiąż ]
Podpunkt 49.1 (1 pkt)
Dane są okrąg i prosta styczna do tego okręgu w punkcie
A .
Punkty
B i
C są położone na okręgu tak,
że
BC jest jego średnicą. Cięciwa
AB
tworzy ze styczną kąt o mierze
53^{\circ} (zobacz rysunek).
Miara stopniowa kąta ABC jest równa:
Odpowiedź:
|\sphericalangle ABC| \ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 50. (1 pkt) (Numer zadania: pp-12095)
[ ⇒ Rozwiąż ]
Podpunkt 50.1 (1 pkt)
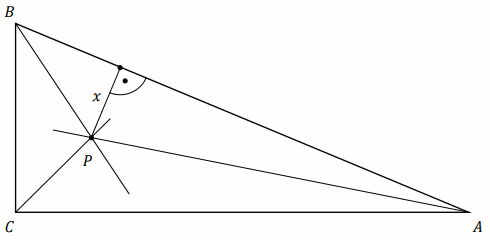
Dany jest trójkąt prostokątny
ABC o bokach
|AC|=48 ,
|BC|=14 ,
|AB|=50 . Dwusieczne kątów tego trójkąta przecinają się w punkcie
P (zobacz rysunek).
Odległość x punktu P od przeciwprostokątnej
AB jest równa:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 51. (1 pkt) (Numer zadania: pp-12096)
[ ⇒ Rozwiąż ]
Podpunkt 51.1 (1 pkt)
Jeden z boków równoległoboku ma długość równą
10 .
Przekątne tego równoległoboku mogą mieć długości:
Odpowiedzi:
A. 10 i 10
B. 8 i 6
C. 20 i 20
D. 8 i 12
Zadanie 52. (1 pkt) (Numer zadania: pp-12098)
[ ⇒ Rozwiąż ]
Podpunkt 52.1 (1 pkt)
W pewnym trójkącie równoramiennym największy kąt ma miarę
120^{\circ} ,
a najdłuższy bok ma długość
6 (zobacz rysunek).
Najkrótsza wysokość tego trójkąta ma długość równą:
Odpowiedź:
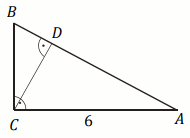
Zadanie 53. (1 pkt) (Numer zadania: pp-12124)
[ ⇒ Rozwiąż ]
Podpunkt 53.1 (1 pkt)
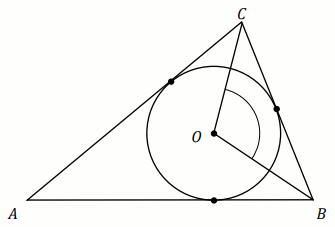
Okrąg o środku w punkcie
O jest wpisany w trójkąt
ABC . Wiadomo, że
|AB|=|AC| i
|\sphericalangle BOC|=124^{\circ} (zobacz rysunek).
Miara stopniowa kąta BAC jest równa:
Odpowiedź:
|\sphericalangle BAC|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 54. (1 pkt) (Numer zadania: pp-12125)
[ ⇒ Rozwiąż ]
Podpunkt 54.1 (1 pkt)
Punkty
A ,
B ,
C i
D leżą na okręgu o środku w punkcie
O .
Cięciwy
DB i
AC przecinają się
w punkcie
E ,
|\sphericalangle ACB|=58^{\circ} oraz
|\sphericalangle AEB|=127^{\circ} (zobacz rysunek).
Miara stopniowa kąta DAC jest równa:
Odpowiedź:
|\sphericalangle DAC|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 55. (1 pkt) (Numer zadania: pp-12126)
[ ⇒ Rozwiąż ]
Podpunkt 55.1 (1 pkt)
Przekątna
AC prostokąta
ABCD ma
długość
\frac{225}{2} . Na boku
AB obrano
punkt
E , na przekątnej
AC obrano punkt
F , a na boku
AD obrano punkt
G – tak, że czworokąt
AEFG jest
prostokątem (zobacz rysunek). Ponadto
|EF|=27 i
|GF|=36 .
Obwód prostokąta ABCD jest równy:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 56. (1 pkt) (Numer zadania: pp-12123)
[ ⇒ Rozwiąż ]
Podpunkt 56.1 (1 pkt)
Czworokąt
ABCD jest wpisany w okrąg o środku
S . Bok
AD jest średnicą tego okręgu,
a miara kąta
BDC jest równa
39^{\circ} (zobacz rysunek).
Wtedy miara stopniowa kąta BSC jest równa:
Odpowiedź:
|\sphericalangle BSC|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 57. (1 pkt) (Numer zadania: pp-12262)
[ ⇒ Rozwiąż ]
Podpunkt 57.1 (1 pkt)
Przyprostokątna
AC trójkąta prostokątnego
ABC
ma długość
6 , a wysokość
CD dzieli go na
dwa takie trójkąty
ADC i
CDB , że pole trójkąta
ADC jest
169 razy większe od pola trójkąta
CDB (zobacz rysunek).
Oblicz długość przyprostokątnej BC tego trójkąta.
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 58. (1 pkt) (Numer zadania: pp-12263)
[ ⇒ Rozwiąż ]
Podpunkt 58.1 (1 pkt)
W trapezie prostokątnym
ABCD są dane długości boków:
|AB|=16 ,
|BC|=50 ,
|DC|=2 ,
|AD|=48 (zobacz rysunek).
Oblicz tangens kąta ostrego ABC .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 59. (1 pkt) (Numer zadania: pp-12264)
[ ⇒ Rozwiąż ]
Podpunkt 59.1 (1 pkt)
Pole trójkąta równoramiennego jest równe
\frac{289}{4} .
Miara kąta między ramionami tego trójkąta jest równa
30^{^\circ} .
Oblicz długość ramienia tego trójkąta.
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 60. (1 pkt) (Numer zadania: pp-12265)
[ ⇒ Rozwiąż ]
Podpunkt 60.1 (1 pkt)
Dany jest trójkąt prostokątny
ABC , w którym przyprostokątna
BC ma długość
215 cm, a przyprostokątna
AB ma długość
42 cm. Miara stopniowa
\beta kąta
BAC zaokrąglona do pełnych
stopni jest równa:
Odpowiedź:
\beta\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 61. (1 pkt) (Numer zadania: pp-12266)
[ ⇒ Rozwiąż ]
Podpunkt 61.1 (1 pkt)
Punkty
A ,
B ,
C ,
D leżą na okręgu o środku w punkcie
O .
Kąt środkowy
DOC ma miarę
126^{\circ} (zobacz rysunek).
Oblicz miarę stopniową kąta ABC .
Odpowiedź:
|\sphericalangle ABC| [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 62. (1 pkt) (Numer zadania: pp-12267)
[ ⇒ Rozwiąż ]
Podpunkt 62.1 (1 pkt)
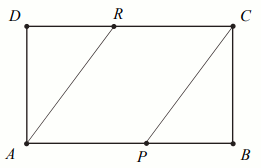
Pole prostokąta
ABCD jest równe
90 .
Na bokach
AB i
CD wybrano – odpowiednio –
punkty
P i
R , takie, że
|AP|:|PB|=|CR|:|RD|=16:3 (zobacz rysunek).
Oblicz pole powierzchni czworokąta APCR .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 63. (1 pkt) (Numer zadania: pp-12268)
[ ⇒ Rozwiąż ]
Podpunkt 63.1 (1 pkt)
Na okręgu o środku w punkcie
O leżą punkty
A ,
B i
C (zobacz rysunek). Kąt
ABC ma miarę
118^{\circ} , a kąt
BOC ma miarę
31^{\circ} .
Oblicz miarę stopniową kąta AOB .
Odpowiedź:
|\sphericalangle AOB|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 64. (1 pkt) (Numer zadania: pp-12269)
[ ⇒ Rozwiąż ]
Podpunkt 64.1 (1 pkt)
W trójkącie
ABC punkt
D leży na boku
BC , a punkt
E leży na boku
AC . Odcinek
DE jest równoległy do boku
AB , a ponadto
|AE|=4 ,
|DE|=\frac{29}{6} ,
|AB|=6 (zobacz rysunek).
Oblicz długość odcinka CE .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 65. (1 pkt) (Numer zadania: pp-12270)
[ ⇒ Rozwiąż ]
Podpunkt 65.1 (1 pkt)
Dany jest trójkąt równoboczny, którego pole powierzchni jest równe
\frac{121\sqrt{3}}{2} .
Bok a tego trójkąta ma długość:
Odpowiedź:
a=
\cdot √
(wpisz dwie liczby całkowite)
Zadanie 66. (1 pkt) (Numer zadania: pp-12271)
[ ⇒ Rozwiąż ]
Podpunkt 66.1 (1 pkt)
Dany jest trójkąt równoramienny
ABC , w którym
|AC|=|BC| . Na podstawie
AB tego trójkąta
leży punkt
D , taki że
|AD|=|CD| ,
|BC|=|BD| oraz
|\sphericalangle BCD|=84^{\circ} (zobacz rysunek).
Wyznacz miarę stopniową kąta ACD .
Odpowiedź:
|\sphericalangle ACD|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 67. (1 pkt) (Numer zadania: pp-12354)
[ ⇒ Rozwiąż ]
Podpunkt 67.1 (1 pkt)
W trójkącie prostokątnym
ABC sinus kąta
CAB jest równy
\frac{28}{53} ,
a przeciwprostokątna
AB jest o
25
dłuższa od przyprostokątnej
BC .
Długość przeciwprostokątnej AB tego trójkąta jest równa:
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)
Zadanie 68. (1 pkt) (Numer zadania: pp-12355)
[ ⇒ Rozwiąż ]
Podpunkt 68.1 (1 pkt)
Dany jest trójkąt
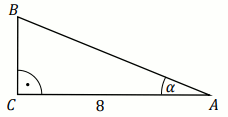
ABC , w którym
|AB|=3 ,
|AC|=6 oraz
\cos\sphericalangle BAC=\frac{2}{3} .
Długość boku BC tego trójkąta jest równa:
Odpowiedź:
Zadanie 69. (1 pkt) (Numer zadania: pp-12356)
[ ⇒ Rozwiąż ]
Podpunkt 69.1 (1 pkt)
Punkty
K ,
L oraz
M
należą do okręgu o środku w punkcie
S . Miara kąta
KSM jest równa
170^{\circ}
(zobacz rysunek).
Miara stopniowa kąta wpisanego w ten okrąg KLM jest równa:
Odpowiedź:
|\sphericalangle KLM|\ [^\circ]=
(wpisz liczbę całkowitą)
Zadanie 70. (1 pkt) (Numer zadania: pp-12376)
[ ⇒ Rozwiąż ]
Podpunkt 70.1 (1 pkt)
Dany jest okrąg o środku w punkcie
S i promieniu
12 .
Miara kąta wpisanego
ACB jest równa
60^{\circ} (zobacz rysunek).
Długość łuku AB , na którym oparty jest kąt wpisany ACB ,
jest równa p\cdot \pi .p .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 71. (1 pkt) (Numer zadania: pp-12391)
[ ⇒ Rozwiąż ]
Podpunkt 71.1 (1 pkt)
Punkty
A ,
B oraz
C
leżą na okręgu o środku w punkcie
O . Miara kąta
BCA jest równa
66^{\circ} (zobacz rysunek).
Miara stopniowa kąta ostrego ABO jest równa:
Odpowiedź:
|\sphericalangle ABO|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 72. (1 pkt) (Numer zadania: pp-12392)
[ ⇒ Rozwiąż ]
Podpunkt 72.1 (1 pkt)
W trójkącie równoramiennym
ABC dane są:
|AC|=|BC|=3 i
|AB|=2 .
Na boku
BC , między punktami
B i
C , wybrano taki punkt
D , że
trójkąty
ABC i
BDA są podobne (zobacz rysunek).
Odcinek BD ma długość:
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 73. (1 pkt) (Numer zadania: pp-12393)
[ ⇒ Rozwiąż ]
Podpunkt 73.1 (1 pkt)
Dany jest trójkąt
ABC , w którym
|AB|=24 ,
|BC|=25 oraz
|\sphericalangle ABC|=60^{\circ} (zobacz rysunek).
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
T/N : pole powierzchni trójkąta ABC jest równe 150\sqrt{3}
T/N : trójkąta ABC ma dwa kąty o tej samej mierze
Zadanie 74. (1 pkt) (Numer zadania: pp-12412)
[ ⇒ Rozwiąż ]
Podpunkt 74.1 (1 pkt)
Dany jest trójkąt prostokątny o kątach ostrych
\alpha oraz
\beta (zobacz rysunek). Sinus kąta
\alpha
jest równy
\frac{1}{4} .
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
T/N : \cos\alpha=\frac{15}{16}
T/N : \sin\beta=\frac{\sqrt{30}}{4}
Zadanie 75. (1 pkt) (Numer zadania: pp-12413)
[ ⇒ Rozwiąż ]
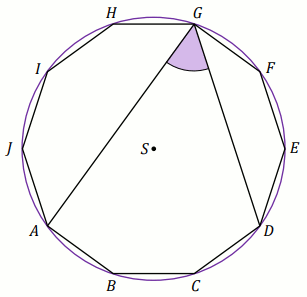
Podpunkt 75.1 (1 pkt)
Na dziesięciokącie foremnym
ABCDEFGHIJ opisano okrąg o środku w
punkcie
S (zobacz rysunek).
Miara stopniowa kąta środkowego okręgu ASD jest równa:
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
Zadanie 76. (1 pkt) (Numer zadania: pp-12414)
[ ⇒ Rozwiąż ]
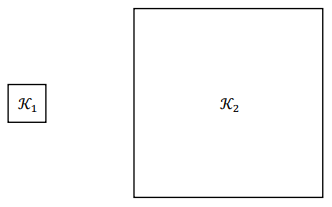
Podpunkt 76.1 (1 pkt)
Kwadrat
K_2 jest podobny do kwadratu
K_1
w skali
8 (zobacz rysunek). Suma pól tych kwadratów jest równa
130 .
Długość a boku kwadratu K_1 jest równa:
Odpowiedź:
Zadanie 77. (1 pkt) (Numer zadania: pp-12435)
[ ⇒ Rozwiąż ]
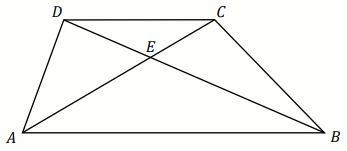
Podpunkt 77.1 (1 pkt)
Dany jest trapez
ABCD o podstawach
AB
i
CD takich, że
|AB|=8\cdot |CD| .
Przekątne
AC i
BD przecinają się w
punkcie
E (zobacz rysunek).
Oceń prawdziwość poniższych zdań.
Odpowiedzi:
T/N : P_{\trangle BCE}=P_{\trangle AED}
T/N : P_{\trangle ABD}=P_{\trangle ABC}
Masz pytania? Napisz: k42195@poczta.fm