Planimetria z CKE

Zadania z matur CKE dla liceum ogólnokształcącego - poziom rozszerzony

Uczeń:

wyznacza promienie i średnice okręgów, długości cięciw okręgów oraz odcinków stycznych, w tym z wykorzystaniem twierdzenia Pitagorasa;
rozpoznaje trójkąty ostrokątne, prostokątne i rozwartokątne przy danych długościach boków (m.in. stosuje twierdzenie odwrotne do twierdzenia Pitagorasa i twierdzenie cosinusów); stosuje twierdzenie: w trójkącie naprzeciw większego kąta wewnętrznego leży dłuższy bok;
rozpoznaje wielokąty foremne i korzysta z ich podstawowych własności;
korzysta z własności kątów i przekątnych w prostokątach, równoległobokach, rombach i trapezach;
stosuje własności kątów wpisanych i środkowych;
stosuje wzory na pole wycinka koła i długość łuku okręgu;
stosuje twierdzenia: Talesa, odwrotne do twierdzenia Talesa, o dwusiecznej kąta oraz o kącie między styczną a cięciwą;
korzysta z cech podobieństwa trójkątów;
wykorzystuje zależności między obwodami oraz między polami figur podobnych;
wskazuje podstawowe punkty szczególne w trójkącie: środek okręgu wpisanego w trójkąt, środek okręgu opisanego na trójkącie, ortocentrum, środek ciężkości oraz korzysta z ich własności;
stosuje funkcje trygonometryczne do wyznaczania długości odcinków w figurach płaskich oraz obliczania pól figur;
przeprowadza dowody geometryczne.

Zadanie 1. (1 pkt) (Numer zadania: pr-21159)

Podpunkt 1.1 (1 pkt)

Dany jest trójkąt prostokątny $ABC$ , w którym $|\sphericalangle ABC|=90^{\circ}$ oraz $|\sphericalangle CAB|=60^{\circ}$ . Punkty $K$ i $L$ leżą na bokach – odpowiednio – $AB$ i $BC$ tak, że $|BK|=|BL|=6$ (zobacz rysunek). Odcinek $KL$ przecina wysokość $BD$ tego trójkąta w punkcie $N$ , a ponadto $|AD|=16$ .

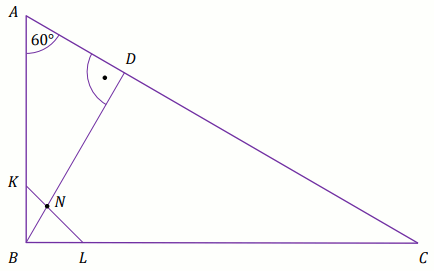
Oblicz, $|ND|$ .

Odpowiedź:

$\|ND\|=$	$+$ $\cdot$ √


(wpisz cztery liczby całkowite)

Zadanie 2. (3 pkt) (Numer zadania: pr-21164)

[ ⇒ Rozwiąż ]

Podpunkt 2.1 (3 pkt)

Dany jest okrąg $\mathcal{O}$ . Przez punkt $A$ poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – $P$ oraz $Q$ . Przez punkt $B$ leżący na odcinku $AP$ poprowadzono styczną do tego okręgu w punkcie $D$ , która przecięła odcinek $AQ$ w punkcie $C$ (zobacz rysunek).

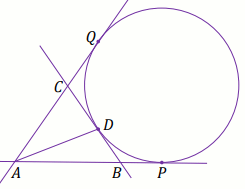
Wiadomo, że $|AQ|=15\cdot |BP|$ oraz $|CD|=7\cdot |BD|$ .

Oblicz $|AC|:|BC|$ .

Odpowiedź:

$\|AC\|:\|BC\|=$

(wpisz dwie liczby całkowite)

Zadanie 3. (3 pkt) (Numer zadania: pr-21177)

[ ⇒ Rozwiąż ]

Podpunkt 3.1 (1 pkt)

Punkt $P$ jest punktem przecięcia przekątnych trapezu $ABCD$ . Długość podstawy $CD$ jest o $3$ mniejsza od długości podstawy $AB$ . Promień okręgu opisanego na trójkącie ostrokątnym $CPD$ jest o $6$ mniejszy od promienia okręgu opisanego na trójkącie $APB$ . Wówczas, spełniony jest warunek: $|DP|^2+|CP|^2-|CD|^2=a\cdot|DP|\cdot|CP|$ .

Wyznacz $\sin\sphericalangle APB$ .

Odpowiedź:

$\sin\sphericalangle APB=$

(wpisz dwie liczby całkowite)

Podpunkt 3.2 (2 pkt)

Wyznacz liczbę $a$ .

Odpowiedź:

$a=$	$\cdot$ √


(wpisz trzy liczby całkowite)

Zadanie 4. (3 pkt) (Numer zadania: pr-21189)

[ ⇒ Rozwiąż ]

Podpunkt 4.1 (3 pkt)

Dany jest trójkąt równoboczny $ABC$ . Na bokach $AB$ i $AC$ wybrano punkty – odpowiednio – $D$ i $E$ takie, że $|BD|=|AE|=\frac{1}{14}|AB|$ . Odcinki $CD$ i $BE$ przecinają się w punkcie $P$ (zobacz rysunek).

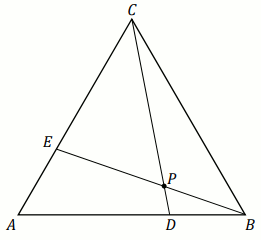
Pole powierzchni trójkąta $ABC$ jest równe. $k\cdot P_{\triangle DBP}$ , gdzie $k$ jest liczbą całkowitą.
Podaj liczbę $k$ .

Odpowiedź:

$k=$ (wpisz liczbę całkowitą)

Zadanie 5. (3 pkt) (Numer zadania: pr-21192)

[ ⇒ Rozwiąż ]

Podpunkt 5.1 (3 pkt)

Dany jest trójkąt $ABC$ . Na boku $AB$ tego trójkąta obrano punkty $D$ , $E$ i $F$ tak, że $|AD|=|DE|=|EF|=16\cdot|FB|$ . Na bokach $AC$ i $BC$ obrano – odpowiednio – punkty $G$ i $H$ tak, że $DG\parallel EC$ oraz $FH\parallel EC$ (zobacz rysunek).

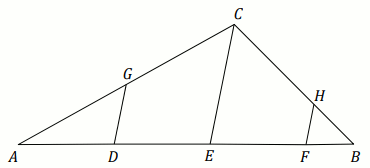
Niech pole trójkąta $FBH$ będzie równe $S$ . Zapisz pole trójkąta $ADG$ w postaci $k\cdot S$ .
Podaj liczbę $k$ .

Odpowiedź:

$k=$

(wpisz dwie liczby całkowite)

Zadanie 6. (3 pkt) (Numer zadania: pr-21195)

[ ⇒ Rozwiąż ]

Podpunkt 6.1 (3 pkt)

W trójkącie $ABC$ kąt $BAC$ jest dwa razy większy od kąta $ABC$ o mierze $\alpha$ . Niech $|BC|=a$ , $|AC|=b$ oraz $|AB|=c$ . Wówczas $\cos\alpha=\frac{m\cdot a}{n\cdot b}$ , gdzie $m, n$ jest są pewnymi liczbami całkowitymi.

Podaj liczby $m$ i $n$ .

Odpowiedzi:

$m$	$=$	(wpisz liczbę całkowitą)
$n$	$=$	(wpisz liczbę całkowitą)

Zadanie 7. (2 pkt) (Numer zadania: pr-21196)

[ ⇒ Rozwiąż ]

Podpunkt 7.1 (2 pkt)

W trójkącie $ABC$ bok $AB$ jest $4$ razy dłuższy od boku $AC$ , a długość boku $BC$ stanowi $\frac{10}{3}$ długości boku $AC$ .

Oblicz cosinus najmniejszego kąta trójkąta $ABC$ .

Odpowiedź:

$\cos\alpha=$

(wpisz dwie liczby całkowite)

Zadanie 8. (3 pkt) (Numer zadania: pr-21198)

[ ⇒ Rozwiąż ]

Podpunkt 8.1 (1 pkt)

Dany jest trójkąt równoramienny $ABC$ , w którym $|AC|=|AB|=39$ , a punkt $D$ jest środkiem podstawy $AB$ . Okrąg o środku $D$ jest styczny do prostej $AC$ w punkcie $M$ . Punkt $K$ leży na boku $AC$ , punkt $L$ leży na boku $BC$ , odcinek $KL$ jest styczny do rozważanego okręgu oraz $|KC|=|LC|=3$ (zobacz rysunek).

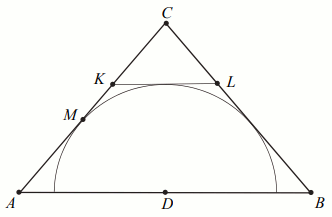
Oblicz $|KL|$ .

Odpowiedź:

$\|KL\|=$

(wpisz dwie liczby całkowite)

Podpunkt 8.2 (2 pkt)

Oblicz $\frac{|AM|}{|MC|}$ .

Odpowiedź:

$\|AM\|:\|MC\|=$

(wpisz dwie liczby całkowite)

Masz pytania? Napisz: k42195@poczta.fm