Planimetria z CKE

Zadania z matur CKE dla liceum ogólnokształcącego - poziom rozszerzony

Uczeń:

wyznacza promienie i średnice okręgów, długości cięciw okręgów oraz odcinków stycznych, w tym z wykorzystaniem twierdzenia Pitagorasa;
rozpoznaje trójkąty ostrokątne, prostokątne i rozwartokątne przy danych długościach boków (m.in. stosuje twierdzenie odwrotne do twierdzenia Pitagorasa i twierdzenie cosinusów); stosuje twierdzenie: w trójkącie naprzeciw większego kąta wewnętrznego leży dłuższy bok;
rozpoznaje wielokąty foremne i korzysta z ich podstawowych własności;
korzysta z własności kątów i przekątnych w prostokątach, równoległobokach, rombach i trapezach;
stosuje własności kątów wpisanych i środkowych;
stosuje wzory na pole wycinka koła i długość łuku okręgu;
stosuje twierdzenia: Talesa, odwrotne do twierdzenia Talesa, o dwusiecznej kąta oraz o kącie między styczną a cięciwą;
korzysta z cech podobieństwa trójkątów;
wykorzystuje zależności między obwodami oraz między polami figur podobnych;
wskazuje podstawowe punkty szczególne w trójkącie: środek okręgu wpisanego w trójkąt, środek okręgu opisanego na trójkącie, ortocentrum, środek ciężkości oraz korzysta z ich własności;
stosuje funkcje trygonometryczne do wyznaczania długości odcinków w figurach płaskich oraz obliczania pól figur;
przeprowadza dowody geometryczne.

Zadanie 1. (4 pkt) (Numer zadania: pr-30877)

Podpunkt 1.1 (4 pkt)

Czworokąt $ABCD$ , w którym $|BC|=20\sqrt{3}$ i $|CD|=25\sqrt{3}$ , jest opisany na okręgu. Przekątna $AC$ tego czworokąta tworzy z bokiem $BC$ kąt o mierze $60^{\circ}$ , natomiast z bokiem $AB$ – kąt ostry, którego sinus jest równy $\frac{1}{4}$ .

Oblicz obwód czworokąta $ABCD$ .

Odpowiedź:

$L_{ABCD}=$ $+$ $\cdot$ √
(wpisz trzy liczby całkowite)

Zadanie 2. (5 pkt) (Numer zadania: pr-30887)

[ ⇒ Rozwiąż ]

Podpunkt 2.1 (2 pkt)

Czworokąt wypukły $ABCD$ jest wpisany w okrąg o promieniu $36$ . Kąty $BAD$ i $BCD$ są proste (zobacz rysunek).

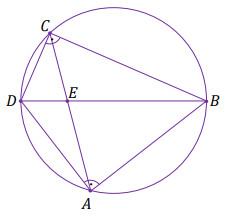
Przekątne $AC$ i $BD$ tego czworokąta przecinają się w punkcie $E$ tak, że $|BE|=3\cdot |DE|$ oraz $|BD|=2\cdot |AE|$ .

Oblicz długość boku $AB$ .

Odpowiedź:

$\|AB\|=$	$\cdot$ √


(wpisz trzy liczby całkowite)

Podpunkt 2.2 (1 pkt)

Oblicz długość boku $AD$ .

Odpowiedź:

$\|AD\|=$	$\cdot$ √


(wpisz trzy liczby całkowite)

Podpunkt 2.3 (2 pkt)

Oblicz długość boku $BC$ .

Odpowiedź:

$\|BC\|=$	$\cdot$ √


(wpisz trzy liczby całkowite)

Zadanie 3. (4 pkt) (Numer zadania: pr-30889)

[ ⇒ Rozwiąż ]

Podpunkt 3.1 (2 pkt)

Dany jest kwadrat $ABCD$ o boku $a$ długości $6$ . Punkt $E$ dzieli bok $CD$ w stosunku $|DE|:|EC|=8:1$ . Przekątna $BD$ dzieli trójkąt $ACE$ na dwie figury: $AGF$ oraz $CEFG$ (zobacz rysunek).

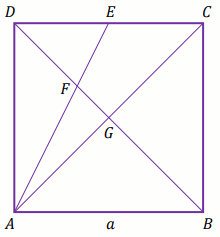
Oblicz pole trójkąta $AGF$ .

Odpowiedź:

$P_{\triangle AGF}=$

(wpisz dwie liczby całkowite)

Podpunkt 3.2 (2 pkt)

Oblicz pole czworokąta $CEFG$ .

Odpowiedź:

$P_{\square CEFG}=$

(wpisz dwie liczby całkowite)

Zadanie 4. (2 pkt) (Numer zadania: pr-30896)

[ ⇒ Rozwiąż ]

Podpunkt 4.1 (2 pkt)

W okrąg o promieniu $20$ wpisano trójkąt $ABC$ . Długość boku $AB$ jest równa $24$ . Bok $BC$ ma długość $20\sqrt{3}$ i jest najdłuższym bokiem tego trójkąta.

Oblicz długość boku $AC$ trójkąta $ABC$ . Jeśli zadanie posiada dwa rozwiązania podaj większe z nich.

Odpowiedź:

$\|AC\|=$	$+$ $\cdot$ √


(wpisz cztery liczby całkowite)

Zadanie 5. (5 pkt) (Numer zadania: pr-31022)

[ ⇒ Rozwiąż ]

Podpunkt 5.1 (1 pkt)

Dany jest trapez $ABCD$ o podstawach $AB$ i $CD$ , w którym $|AB|>|CD|$ oraz ramię $BC$ ma długość $\frac{13}{4}$ . Na tym trapezie opisano okrąg o promieniu $R=\frac{481}{96}$ . Miary kątów $BAC$ i $ABC$ tego trapezu spełniają warunek $\frac{\sin\sphericalangle BAC}{\sin\sphericalangle ABC}=\frac{13}{37}$ .

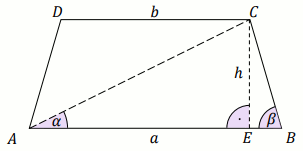
Oblicz $\sin\alpha$ .

Odpowiedź:

$\sin\alpha=$

(wpisz dwie liczby całkowite)

Podpunkt 5.2 (1 pkt)

Oblicz wysokość trapezu $h$ .

Odpowiedź:

$h=$

(wpisz dwie liczby całkowite)

Podpunkt 5.3 (1 pkt)

Oblicz długość przekątnej $AC$ .

Odpowiedź:

$\|AC\|=$

(wpisz dwie liczby całkowite)

Podpunkt 5.4 (1 pkt)

Oblicz długość podstawy $AB$ .

Odpowiedź:

$\|AB\|=$

(wpisz dwie liczby całkowite)

Podpunkt 5.5 (1 pkt)

Oblicz pole trapezu $ABCD$ .

Odpowiedź:

$\|AB\|=$

(wpisz dwie liczby całkowite)

Zadanie 6. (4 pkt) (Numer zadania: pr-31029)

[ ⇒ Rozwiąż ]

Podpunkt 6.1 (1 pkt)

Dany jest trapez równoramienny $ABCD$ o obwodzie $l$ i podstawach $AB$ oraz $CD$ takich, że $|AB|> |CD|$ . Trapez jest opisany na okręgu i wpisany w okrąg, a wysokość $CE$ trapezu ma długość $h$ (zobacz rysunek).

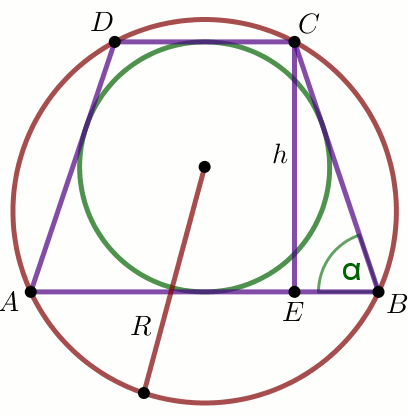
Sinus kąta $\alpha$ jest równy $\sin\alpha=\frac{a\cdot h}{l}$ .
Podaj liczbę $a$ .

Odpowiedź:

$a=$ (wpisz liczbę całkowitą)

Podpunkt 6.2 (3 pkt)

Długość promienia $R$ okręgu opisanego na tym trapezie wyraża się wzorem $R=\frac{l\cdot\sqrt{a\cdot h^2+l^2}}{b\cdot h}$ .

Podaj liczby $a$ i $b$ .

Odpowiedzi:

$a$	$=$	(wpisz liczbę całkowitą)
$b$	$=$	(wpisz liczbę całkowitą)

Zadanie 7. (4 pkt) (Numer zadania: pr-30381)

[ ⇒ Rozwiąż ]

Podpunkt 7.1 (4 pkt)

Na przeciwprostokątnej $AB$ trójkąta prostokątnego $ABC$ zbudowano kwadrat $ABDE$ (zobacz rysunek).

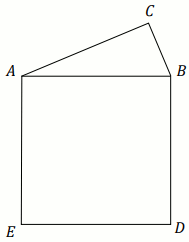
Jeden z kątów ostrych $\alpha$ tego trójkąta spełnia warunek $\sin{2\alpha}=\frac{1}{3}$ .

Oblicz stosunek pola kwadratu $AEDB$ do pola trójkąta $ABC$ .

Odpowiedź:

$P_{AEDB}:P_{ABC}=$

(wpisz dwie liczby całkowite)

Zadanie 8. (4 pkt) (Numer zadania: pr-31033)

[ ⇒ Rozwiąż ]

Podpunkt 8.1 (2 pkt)

Czworokąt $ABCD$ jest wpisany w okrąg o promieniu $R=4$ . Przekątna $BD$ tego czworokąta ma długość $4\sqrt{3}$ . Kąty wewnętrzne $BAD$ i $ADC$ czworokąta $ABCD$ są ostre, a iloczyn sinusów wszystkich jego kątów wewnętrznych jest równy $\frac{3}{16}$ .

Podaj miarę stopniową kąta $BCD$ .

Odpowiedź:

$|\sphericalangle BCD| \ [^{\circ}]=$ (wpisz liczbę całkowitą)

Podpunkt 8.2 (2 pkt)

Podaj miarę stopniową kąta $CDA$ .

Odpowiedź:

$|\sphericalangle CDA| \ [^{\circ}]=$ (wpisz liczbę całkowitą)

Zadanie 9. (4 pkt) (Numer zadania: pr-31045)

[ ⇒ Rozwiąż ]

Podpunkt 9.1 (2 pkt)

Dany jest trójkąt prostokątny $ABC$ . Promień okręgu wpisanego w ten trójkąt jest równy $8$ i jest o $32$ krótszy od przeciwprostokątnej tego trójkąta.

Oblicz iloczyn długości przyprostokątnych tego trójkata.

Odpowiedź:

$a\cdot b=$ (wpisz liczbę całkowitą)

Podpunkt 9.2 (2 pkt)

Oblicz sinus większego z kątów ostrych tego trójkąta.

Odpowiedź:

$\sin\alpha=$

(wpisz dwie liczby całkowite)

Zadanie 10. (5 pkt) (Numer zadania: pr-31054)

[ ⇒ Rozwiąż ]

Podpunkt 10.1 (2 pkt)

Na okręgu jest opisany czworokąt $ABCD$ . Bok $AD$ tego czworokąta jest $2$ razy dłuższy od boku $AB$ , a przekątna $BD$ ma długość równą $8$ . Ponadto spełnione są następujące warunki: $\cos\sphericalangle ADB=\frac{139}{160}$ , $|\sphericalangle BCD|=90^{\circ}$ oraz $|AB|$ jest liczbą całkowitą.

Oblicz długość boku $AB$ tego czworokąta.

Odpowiedź:

$|AB|=$ (wpisz liczbę całkowitą)

Podpunkt 10.2 (3 pkt)

Podaj długość krótszej z przyprostokątnych trójkąta $BCD$ .

Odpowiedź:

$\|BC\|=$	$+$ $\cdot$ √


(wpisz cztery liczby całkowite)

Zadanie 11. (5 pkt) (Numer zadania: pr-31058)

[ ⇒ Rozwiąż ]

Podpunkt 11.1 (2 pkt)

Trapez prostokątny $ABCD$ o podstawach $AB$ i $CD$ jest opisany na okręgu. Ramię $BC$ ma długość $10$ , a ramię $AD$ jest wysokością trapezu. Podstawa $AB$ jest $9$ razy dłuższa od podstawy $CD$ .

Oblicz długość krótszej podstawy tego trapezu.

Odpowiedź:

$\|CD\|=$

(wpisz dwie liczby całkowite)

Podpunkt 11.2 (2 pkt)

Oblicz wysokość tego trapezu.

Odpowiedź:

$h=$

(wpisz dwie liczby całkowite)

Podpunkt 11.3 (1 pkt)

Oblicz pole powierzchni tego trapezu.

Odpowiedź:

$P_{ABCD}=$

(wpisz dwie liczby całkowite)

Zadanie 12. (6 pkt) (Numer zadania: pr-31073)

[ ⇒ Rozwiąż ]

Podpunkt 12.1 (2 pkt)

Dany jest romb $ABCD$ . Przez wierzchołki $B$ i $D$ poprowadzono dwie proste równoległe przecinające boki $CD$ i $AB$ – odpowiednio – w punktach $M$ i $N$ , tak, że podzieliły one boki rombu w stosunku $|AN|:|NB|=|CM|:|MD|=4:1$ . Ponadto wiadomo, że $|MB|=|ND|=|BD|$ (zobacz rysunek).

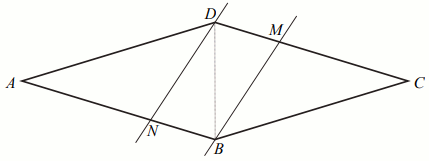
Oblicz stosunek pól powierzchni trójkąta $AND$ do czworokata $NBMD$ .

Odpowiedź:

$\frac{P_{AND}}{P_{NBMD}}=$

(wpisz dwie liczby całkowite)

Podpunkt 12.2 (4 pkt)

Oblicz cosinus kąta $BCD$ .

Odpowiedź:

$\cos\sphericalangle BCD=$

(wpisz dwie liczby całkowite)

Masz pytania? Napisz: k42195@poczta.fm