Stereometria z CKE
Zadania z matur CKE dla liceum ogólnokształcącego - poziom podstawowy
Uczeń:
- rozpoznaje wzajemne położenie prostych w przestrzeni, w szczególności proste prostopadłe nieprzecinające się;
- posługuje się pojęciem kąta między prostą a płaszczyzną oraz pojęciem kąta dwuściennego między półpłaszczyznami;
- rozpoznaje w graniastosłupach i ostrosłupach kąty między odcinkami (np. krawędziami, krawędziami i przekątnymi) oraz kąty między ścianami, oblicza miary tych kątów;
- rozpoznaje w walcach i w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami (np. kąt rozwarcia stożka, kąt między tworzącą a podstawą), oblicza miary tych kątów;
- określa, jaką figurą jest dany przekrój prostopadłościanu płaszczyzną;
- oblicza objętości i pola powierzchni graniastosłupów, ostrosłupów, walca, stożka i kuli, również z wykorzystaniem trygonometrii i poznanych twierdzeń;
- wykorzystuje zależność między objętościami brył podobnych.
| Zadanie 1. (2 pkt) (Numer zadania: pp-21089) | [ ⇒ Rozwiąż ] |
Podpunkt 1.1 (1 pkt)
Dany jest ostrosłup, którego podstawą jest kwadrat o boku długości 6.
Jedna z krawędzi bocznych tego ostrosłupa ma długość 8 i jest prostopadła
do płaszczyzny jego podstawy.
Wyznacz objętość tego ostrosłupa.
Odpowiedź:
| V= | |
Podpunkt 1.2 (1 pkt)
Tangens kąta nachylenia najdłuższej krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy jest równy:
Odpowiedź:
| \tan\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 2. (2 pkt) (Numer zadania: pp-21060) | [ ⇒ Rozwiąż ] |
Podpunkt 2.1 (1 pkt)
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 2\sqrt{3}.
Pole powierzchni całkowitej tego graniastosłupa jest równe:
Odpowiedź:
P_c=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
Podpunkt 2.2 (1 pkt)
Oblicz cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy
tego graniastosłupa.
Odpowiedź:
| Wpisz odpowiedź: | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 3. (3 pkt) (Numer zadania: pp-21065) | [ ⇒ Rozwiąż ] |
Podpunkt 3.1 (1 pkt)
Objętość ostrosłupa prawidłowego czworokątnego jest równa 64.
Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze
\alphataki, że \tan\alpha=\frac{3}{4} (zobacz rysunek).
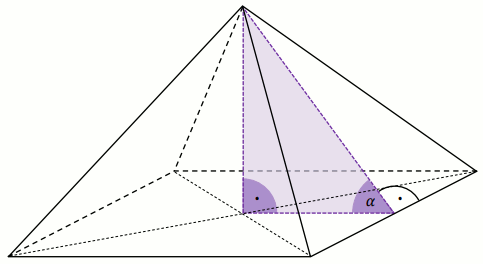

Oblicz długość krawędzi podstawy tego ostrosłupa.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 3.2 (1 pkt)
Oblicz długość wysokości tego ostrosłupa.
Odpowiedź:
H=
(wpisz liczbę całkowitą)
Podpunkt 3.3 (1 pkt)
Oblicz długość wysokości ściany bocznej tego ostrosłupa.
Odpowiedź:
h=
(wpisz liczbę całkowitą)
| Zadanie 4. (3 pkt) (Numer zadania: pp-21088) | [ ⇒ Rozwiąż ] |
Podpunkt 4.1 (3 pkt)
Każda z krawędzi podstawy trójkątnej ostrosłupa ma długość
3\sqrt{3}, a każda jego krawędź boczna ma długość
4.
Oblicz wysokość tego ostrosłupa.
Odpowiedź:
H=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 5. (3 pkt) (Numer zadania: pp-21099) | [ ⇒ Rozwiąż ] |
Podpunkt 5.1 (1 pkt)
Dany jest sześcian ABCDEFGH o krawędzi długości
4. Wierzchołki podstawy ABCD
sześcianu połączono odcinkami z punktem W, który jest
punktem przecięcia przekątnych podstawy EFGH.
Otrzymano w ten sposób ostrosłup prawidłowy czworokątny ABCDW
(zobacz rysunek).
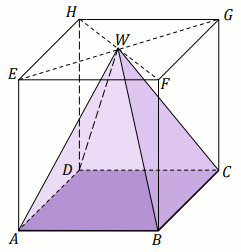

Objętość V ostrosłupa ABCDW jest równa:
Odpowiedź:
| V= | |
Podpunkt 5.2 (2 pkt)
Oblicz cosinus kąta \alpha nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Odpowiedź:
| \cos\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 6. (2 pkt) (Numer zadania: pp-21105) | [ ⇒ Rozwiąż ] |
Podpunkt 6.1 (1 pkt)
Wysokość graniastosłupa prawidłowego sześciokątnego jest równa 6 (zobacz rysunek).
Pole podstawy tego graniastosłupa jest równe \frac{75\sqrt{3}}{2}.
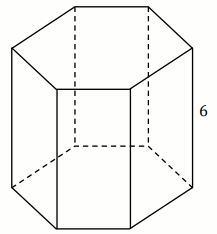

Pole powierzchni jednej ściany bocznej tego graniastosłupa jest równe:
Odpowiedź:
P_{sb}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 6.2 (1 pkt)
Kąt nachylenia najdłuższej przekątnej graniastosłupa prawidłowego sześciokątnego do
płaszczyzny jego podstawy jest zaznaczony na rysunku:
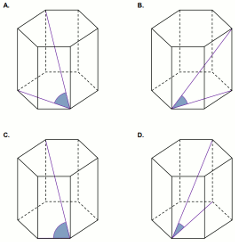

Odpowiedzi:
| A. C | B. D |
| C. B | D. A |
| Zadanie 7. (2 pkt) (Numer zadania: pp-21185) | [ ⇒ Rozwiąż ] |
Podpunkt 7.1 (2 pkt)
Objętość stożka o wysokości 4 jest równa
\frac{64}{9}\pi.
Oblicz miarę stopniową kąta rozwarcia tego stożka.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 8. (3 pkt) (Numer zadania: pp-21196) | [ ⇒ Rozwiąż ] |
Podpunkt 8.1 (1 pkt)
Tworząca stożka ma długość 4. Kąt rozwarcia tego stożka
ma miarę 60^{\circ}.
Obwód podstawy tego stożka ma długość p\cdot \pi. Wyznacz liczbę p.
Odpowiedź:
p=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 8.2 (2 pkt)
Objętośc tego stożka jest równa p\cdot \pi. Wyznacz liczbę p.
Odpowiedź:
| p= | ||
| (wpisz trzy liczby całkowite) | ||