Podgląd arkusza : lo2@am-2-2022-09-18-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10169 |
Podpunkt 1.1 (1 pkt)
« Wyznacz iloczyn wszystkich rozwiązań równania
(x-7)(x+3)(x^2-25)=0.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10414 |
Podpunkt 2.1 (1 pkt)
« Liczbę 4^{17}\cdot 32^{34} można zapiać w postaci:
Odpowiedzi:
| A. 8^{51} | B. 64^{17} |
| C. 8^{68} | D. 4^{85} |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10276 |
Podpunkt 3.1 (1 pkt)
Które z poniższych wzorów opisują funkcję malejącą?
Odpowiedzi:
| T/N : f(x)=\sqrt{x-\frac{1}{5}} | T/N : f(x)=-1+2x |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11431 |
Podpunkt 4.1 (1 pkt)
Liczba 5 jest miejscem zerowym funkcji liniowej
f(x)=.....\cdot x+b, a punkt
M=(-1,-12) należy do wykresu tej funkcji.
Podaj brakującą liczbę.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11114 |
Podpunkt 5.1 (1 pkt)
Wykres proporcjonalności odwrotnej zawiera punkt o współrzednych
(8,3).
Wynika z tego, że ten wykres zawiera też punkt:
Odpowiedzi:
| A. (1,-8) | B. (7,-5) |
| C. (-2,-12) | D. (-4,-3) |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11560 |
Podpunkt 6.1 (1 pkt)
« Które z podanych trójek są długościami boków trójkąta ostrokątnego?
Odpowiedzi:
| T/N : 14, 14, 20 | T/N : 8, 10, 12 |
| T/N : 4, 6, 8 |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11435 |
Podpunkt 7.1 (1 pkt)
Trójkąt T_1 o bokach długości
2\sqrt{7}, 3\sqrt{7} i
4\sqrt{7} jest podobny do trójkąta
T_2. Trójkąt T_2 ma boki
o długościach:
Odpowiedzi:
| A. \frac{4\sqrt{7}}{5},\frac{9\sqrt{7}}{5},\frac{8\sqrt{7}}{5} | B. \frac{4\sqrt{7}}{5},\frac{6\sqrt{7}}{5},\frac{12\sqrt{7}}{5} |
| C. \frac{6\sqrt{7}}{5},\frac{9\sqrt{7}}{5},\frac{12\sqrt{7}}{5} | D. \frac{6\sqrt{7}}{5},\frac{9\sqrt{7}}{5},\frac{8\sqrt{7}}{5} |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10623 |
Podpunkt 8.1 (1 pkt)
« Wiadomo, że \alpha i \beta
są miarami kątów ostrych trójkąta prostokątnego oraz
36\sin^2\alpha+\cos^2\beta=1.
Oblicz \tan\alpha.
Odpowiedź:
| \tan\alpha= | |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10774 |
Podpunkt 9.1 (1 pkt)
Na rysunku przedstawiony jest wykres funkcji
y=f(x).
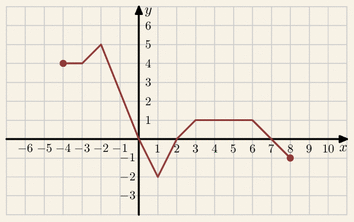
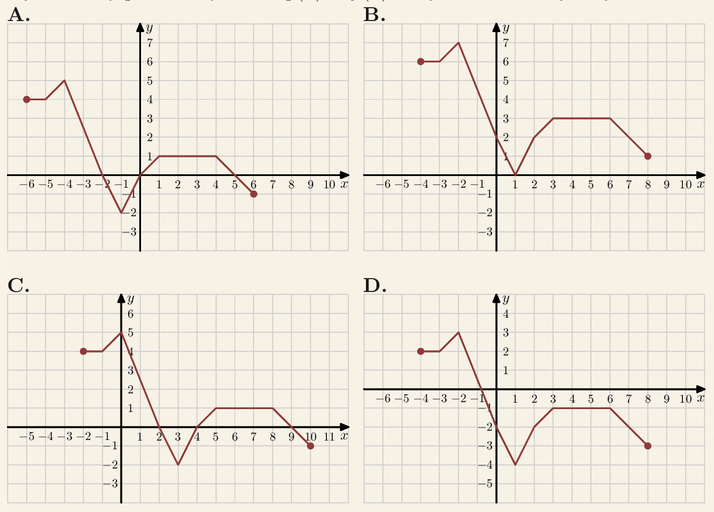

Na którym rysunku przedstawiony jest wykres funkcji y=f(x)-2:

Odpowiedzi:
| A. C | B. B |
| C. D | D. A |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10378 |
Podpunkt 10.1 (1 pkt)
Funkcja f określona jest wzorem
f(x)=|x+1| w przedziale x\in(-6,0),
a wykres funkcji g
otrzymano przesuwając wykres funkcji f o wektor
\vec{u}=[2,-9].
Podaj najmniejszą wartość funkcji f oraz najmniejszą wartość funkcji g.
Odpowiedzi:
| f_{min} | = |
(wpisz liczbę zapisaną dziesiętnie) |
| g_{min} | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20069 |
Podpunkt 11.1 (2 pkt)
Rozwiąż równanie
1\frac{1}{3}=\frac{3x-4}{x-3}
.
Podaj x.
Odpowiedź:
| x= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20308 |
Podpunkt 12.1 (2 pkt)
Miejscem zerowym funkcji f(x)=\frac{2-7m}{2}x+2 jest
liczba \frac{1}{17}.
Wyznacz m.
Odpowiedź:
| m= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20485 |
Podpunkt 13.1 (2 pkt)
Do wykresu funkcji f(x)=\frac{a}{x-3} należy punkt
\left(5,\frac{1}{4}\right) oraz
punkt (x_0,-5).
Wyznacz x_0.
Odpowiedź:
| x_0= | |
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20710 |
Podpunkt 14.1 (2 pkt)
« W trójkącie ABC kąt przy wierzchołku
A jest prosty. Odcinek
AE jest środkową tego trójkąta, zaś
odcinek AF jego wysokością.
Oblicz |EF|.
Dane
|AB|=24
|AC|=7
|AC|=7
Odpowiedź:
| |EF|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20788 |
Podpunkt 15.1 (2 pkt)
» W trójkącie ABC kąt przy wierzchołku
A jest prosty. Wysokość tego trojkąta opuszczona
z wierzchołka kąta prostego dzieli przeciwprostokątną na odcinki
BD i DC, których stosunek
długości jest większy od 1.
Oblicz |BD|:|DC|.
Dane
|AB|:|AC|=5:3=1.66666666666667
Odpowiedź:
| |BD|:|DC|= | |
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20741 |
Podpunkt 16.1 (2 pkt)
Oblicz
(\tan\alpha-\sin\beta)(\cot\alpha-\cos\gamma)
.
Dane
\alpha=45^{\circ}
\beta=30^{\circ}
\gamma=60^{\circ}
\beta=30^{\circ}
\gamma=60^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20742 |
Podpunkt 17.1 (2 pkt)
«« Kąt \alpha jest kątem rozwartym. Wyznacz rozwiązanie
równania
(x-b)\cos^2\alpha=x+\tan\alpha+1-b
.
Dane
b=-3
\sin\alpha=\frac{\sqrt{2}}{2}=0.70710678118655
\sin\alpha=\frac{\sqrt{2}}{2}=0.70710678118655
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20572 |
Podpunkt 18.1 (1 pkt)
« Wyznacz dziedzinę funkcji:
f(x)=\frac{x+4}{x\sqrt{ax+b}}-\frac{2x+4}{x^2+cx+d}
.
Rozwiązanie zapisz w postaci sumy przedziałów. Ile jest tych przedziałów?
Dane
a=5
b=4
c=-8
d=16
b=4
c=-8
d=16
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 18.2 (1 pkt)
Podaj najmniejszy z końców tych przedziałów.
Odpowiedź:
| min= | |
| Zadanie 19. (3 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-21198 |
Podpunkt 19.1 (1 pkt)
Dany jest trójkąt równoramienny ABC, w którym
|AC|=|AB|=14, a punkt D jest środkiem podstawy
AB. Okrąg o środku D jest styczny do prostej
AC w punkcie M. Punkt K
leży na boku AC, punkt L leży na boku
BC, odcinek KL jest styczny do rozważanego okręgu
oraz |KC|=|LC|=2 (zobacz rysunek).
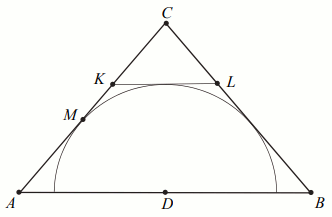

Oblicz |KL|.
Odpowiedź:
| |KL|= | |
Podpunkt 19.2 (2 pkt)
Oblicz \frac{|AM|}{|MC|}.
Odpowiedź:
| |AM|:|MC|= | |
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20578 |
Podpunkt 20.1 (1 pkt)
Funkcja f określona jest wzorem
f(x)=\frac{3}{x+3}+1 w zbiorze
\langle -5,-3)\cup(-3,2\rangle, a funkcja g
wzorem g(x)=-2\cdot f(x).
Zbiorem wartości funkcji g jest zbiór
\mathbb{R}-(p,q).
Wyznacz liczbę p.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 20.2 (1 pkt)
Wyznacz liczbę q.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)