Podgląd arkusza : lo2@am-2-2022-10-02-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10111 |
Podpunkt 1.1 (1 pkt)
Liczby a i b są dodatnie.
13\% liczby a jest równe
65\% liczby b. Wynika stąd,
że:
Odpowiedzi:
| A. liczba b jest 6 razy mniejsza od liczby a | B. liczba a jest 5 razy większa od liczby b |
| C. liczba b jest 7 razy większa od liczby a | D. liczba a jest 6 razy większa od liczby b |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11461 |
Podpunkt 2.1 (1 pkt)
Oblicz liczbę odwrotną do liczby
\sqrt{9+6\sqrt{2}}\cdot\sqrt{9-6\sqrt{2}}.
Odpowiedź:
| \frac{m\sqrt{n}}{k}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11390 |
Podpunkt 3.1 (1 pkt)
Do zbioru wartości funkcji f(x)=4-|x|, gdzie
x\in\mathbb{N} należy liczba:
Odpowiedzi:
| A. 8 | B. \frac{2}{7} |
| C. 6 | D. 1 |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10918 |
Podpunkt 4.1 (1 pkt)
« Funkcja liniowa określona wzorem f(x)=ax+b jest malejąca i ma
miejsce zerowe \frac{\sqrt{35}-6}{2}.
Wynika z tego, że:
Odpowiedzi:
| A. a > 0 \wedge b > 0 | B. a > 0 \wedge b \lessdot 0 |
| C. a \lessdot 0 \wedge b < 0 | D. a \lessdot 0 \wedge b > 0 |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10870 |
Podpunkt 5.1 (1 pkt)
Układ równań
\begin{cases}
2x-y=1\\
-4x+2y=-2
\end{cases}
opisuje w układzie współrzędnych na płaszczyźnie:
Odpowiedzi:
| A. zbiór pusty | B. zbiór jednoelementowy |
| C. zbiór dwuelementowy | D. zbiór nieskończony |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11117 |
Podpunkt 6.1 (1 pkt)
Dla której z podanych wartości a, wykres funkcji określonej wzorem
f(x)=\frac{a}{x} nie ma punktów wspólnych z wykresem
prostej o równaniu y=9x:
Odpowiedzi:
| A. a=\frac{1}{2} | B. a=\frac{1}{4} |
| C. a=3 | D. a=-\sqrt{6} |
| E. a=\frac{1}{5} | F. a=\sqrt{3} |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10601 |
Podpunkt 7.1 (1 pkt)
Odcinki BC i EF
na rysunku są równoległe, przy czym
|AC|=\frac{13}{2} i
|BC|=12:
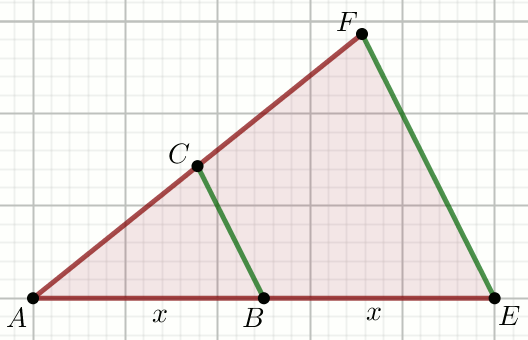

Oblicz długość odcinka EF.
Odpowiedź:
|EF|=
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10660 |
Podpunkt 8.1 (1 pkt)
» W trapezie prostokątnym ABCD długość
ramienia BC jest dwa razy większa od różnicy
długości jego podstaw.
Wyznacz miarę stopniową kąta ABC.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10779 |
Podpunkt 9.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji
y=f(x):
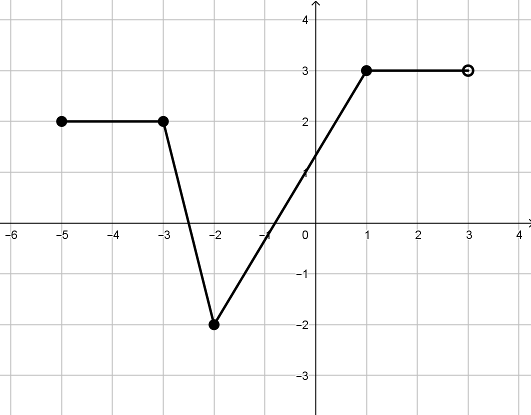
Dziedziną funkcji y=-f(x) jest zbiór:

Odpowiedzi:
| A. \langle -3,5\rangle | B. \langle -5,3\rangle |
| C. \langle -5,3) | D. (-3,5\rangle |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10192 |
Podpunkt 10.1 (1 pkt)
« Wyznacz największą liczbę całkowitą dodatnią spełniającą nierówność
|x+3| \lessdot 22.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20099 |
Podpunkt 11.1 (2 pkt)
Rozwiąż równanie 2x+2(3x+3)-5=-1 o niewiadomej
x.
Odpowiedź:
| x= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20145 |
Podpunkt 12.1 (1 pkt)
« Liczba m+n\sqrt{b}, gdzie
m,n\in\mathbb{C}, spełnia równanie
ax-c=\sqrt{b}x-1.
Podaj m.
Dane
a=4
b=10
c=13
b=10
c=13
Odpowiedź:
m=
(wpisz liczbę całkowitą)
Podpunkt 12.2 (1 pkt)
Podaj n.
Odpowiedź:
n=
(wpisz liczbę całkowitą)
| Zadanie 13. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30009 |
Podpunkt 13.1 (4 pkt)
« « Autobus jechał ze średnią prędkością 60 km/h przez
p całej trasy. Pozostałą część trasy pokonał ze
średnią prędkością 80 km/h.
Oblicz średnią prędkość tego autobusu na całej trasie.
Dane
p=\frac{2}{9}=0.22222222222222
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20771 |
Podpunkt 14.1 (1 pkt)
« Wyznacz dziedzinę funkcji:
f(x)=\frac{\sqrt{x+a}}{\sqrt{b-x}}
.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę wszystkich końców liczbowych tych przedziałów.
Dane
a=17
b=14
b=14
Odpowiedź:
suma=
(wpisz liczbę całkowitą)
Podpunkt 14.2 (1 pkt)
Ile liczb całkowitych jedno lub dwucyfrowych należy do dziedziny
tej funkcji.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 15. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30044 |
Podpunkt 15.1 (2 pkt)
« Dana jest funkcja f(x)=2x+2, której dziedziną
jest zbiór rozwiązań nierówności
(6x+3)^2 \lessdot 36(x-2)^2. Wyznacz
ZW_f.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 15.2 (2 pkt)
Ile liczb naturalnych należy do tego zbioru wartości?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20325 |
Podpunkt 16.1 (2 pkt)
» Rozwiąż układ równań
\begin{cases}
3x+2y=3 \\
y+2=\frac{3(1-x)+4}{2}
\end{cases}
.
Punkt A=(6, m) należy do rozwiązania. Podaj m.
Odpowiedź:
| \frac{p}{q}= | |
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20873 |
Podpunkt 17.1 (2 pkt)
Obwód trójkąta prostokątnego ma długość 27, a
stosunek długość przyprostokątnych tego trójkąta jest równy
3:4.
Oblicz długość przeciwprostokątnej tego trójkąta.
Odpowiedź:
| c= | |
| Zadanie 18. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30299 |
Podpunkt 18.1 (2 pkt)
« Wyznacz długości środkowych trójkąta ABC.
Podaj długość najkrótszej z środkowych tego trójkąta.
Dane
|AC|=52
|BC|=52
|AB|=96
|BC|=52
|AB|=96
Odpowiedź:
| d_{min}= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 18.2 (2 pkt)
Podaj długość najdłuższej z środkowych tego trójkąta.
Odpowiedź:
| d_{max}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20266 |
Podpunkt 19.1 (2 pkt)
» Wiedząc, że \tan\alpha=a, oblicz
\frac{3\sin\alpha\cos\alpha-2\sin^2\alpha}
{7\cos^2\alpha-3\sin\alpha\cos\alpha}
.
Dane
a=\frac{2}{9}=0.222222222222
Odpowiedź:
| m\sqrt{n}= | |
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21034 |
Podpunkt 20.1 (2 pkt)
Rozwiąż nierówność podwójną 2-|2x-1|\leqslant 2|-1+2x|\leqslant 4.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy i największy z końców liczbowych tych przedziałów.
Odpowiedzi:
| min | = |
(wpisz liczbę zapisaną dziesiętnie) |
| max | = |
(wpisz liczbę zapisaną dziesiętnie) |