Podgląd arkusza : lo2@am-2-2022-10-02-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10076 |
Podpunkt 1.1 (1 pkt)
Wyznacz największą liczbę całkowitą spełniającą nierówność
-3\leqslant 7-\frac{2}{5}x\leqslant 3.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10400 |
Podpunkt 2.1 (1 pkt)
Zapisz wyrażenie
\left(\sqrt[3]{9}\cdot 3^{-2}\right)^{6}
w postaci potęgi o podstawie 3.
Podaj wykładnik tej potęgi.
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10281 |
Podpunkt 3.1 (1 pkt)
» Które z poniższych wzorów opisują funkcję nieparzystą?
Odpowiedzi:
| T/N : f(x)=\frac{x^4+2x^2}{x^4-81} | T/N : f(x)=\frac{x^2+3x}{x^2+4} |
| T/N : f(x)=\frac{x^2-4}{|x-2|} |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10866 |
Podpunkt 4.1 (1 pkt)
Wskaż układ nieoznaczony:
Odpowiedzi:
| A. -8x+7y=4\ \wedge\ 8x-7y=-4 | B. -6y-4x=8\ \wedge\ 8x+3y=2 |
| C. -2x+2y=4\ \wedge\ -4y+4x=4 | D. 2x+2y=-5\ \wedge\ -7x-7y=1 |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11623 |
Podpunkt 5.1 (1 pkt)
Wierzchołek paraboli ma współrzedne W=(-4,-5),
a punkt A=\left(-\frac{1}{2}, -10\right) należy do jej
wykresu. Punkt B=(x_B,y_B) też należy do tego wykresu i
jest symetryczny do punktu A względem osi symetrii tej paraboli.
Wyznacz współrzedne punktu B.
Odpowiedzi:
| x_B | = | (dwie liczby całkowite) | |
| y_B | = | (wpisz liczbę całkowitą) | |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10583 |
Podpunkt 6.1 (1 pkt)
« Trójkąt równoramienny prostokątny ma przeciwprostokątną długości
3+4\sqrt{2}.
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11510 |
Podpunkt 7.1 (1 pkt)
Punkt S=(2,-4) jest środkiem odcinka
AB takiego, że punkt A=(x_A, y_A)
należy do osi Oy, a punkt B=(x_B, y_B)
należy do osi Ox.
Wyznacz współrzędne y_A i x_B.
Odpowiedzi:
| y_A | = |
(wpisz liczbę całkowitą) |
| x_B | = |
(wpisz liczbę całkowitą) |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10623 |
Podpunkt 8.1 (1 pkt)
« Wiadomo, że \alpha i \beta
są miarami kątów ostrych trójkąta prostokątnego oraz
16\sin^2\alpha+\cos^2\beta=1.
Oblicz \tan\alpha.
Odpowiedź:
| \tan\alpha= | |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10382 |
Podpunkt 9.1 (1 pkt)
Zbiorem wartości funkcji określonej wzorem y=f(x) jest przedział
liczbowy \langle -5, 2\rangle, a zbiorem wartości funkcji
określonej wzorem y=|f(x)| przedział
\langle p,q\rangle.
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10190 |
Podpunkt 10.1 (0.2 pkt)
« Rozwiązaniem nierówności
|x+4| > 3
jest zbiór liczbowy postaci:
Odpowiedzi:
| A. \langle p,q) | B. \langle p,q\rangle |
| C. (p,q\rangle | D. (p,q) |
| E. (-\infty,p)\cup(q,+\infty) | F. (p,+\infty) |
Podpunkt 10.2 (0.8 pkt)
Rozwiązanie nierówności zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych
tych przedziałów.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20167 |
Podpunkt 11.1 (1 pkt)
Rozwiąż równanie z niewiadomą x:
(-38+6x)(x-5)+(6x-38)(-20+4x)=0
.
Podaj najmniejsze z rozwiązań tego równania.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 11.2 (1 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
| x_{max}= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20293 |
Podpunkt 12.1 (2 pkt)
» Dla jakich wartości parametru m\in\mathbb{R} wykresy funkcji
f(x)=\frac{2x+m}{x-6} oraz
g(x)=-5^{x-1} przecinają oś
Oy w tym samym punkcie.
Podaj najmniejszą możliwą wartość parametru m.
Odpowiedź:
| m_{min}= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20838 |
Podpunkt 13.1 (1 pkt)
Jeśli do liczby 49 dopiszemy cyfrę z przodu, to otrzymamy
liczbę x. Jeśli do liczby 49
dopiszemy cyfrę z tyłu, to otrzymamy liczbę y. Różnica
x-y jest równa 355, zaś suma
cyfr dopisanych z przodu i z tyłu jesty równa 12.
Podaj x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 13.2 (1 pkt)
Podaj liczbę y.
Odpowiedź:
y=
(wpisz liczbę całkowitą)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20251 |
Podpunkt 14.1 (2 pkt)
« W trapezie dane są długości podstaw i ramion:
|CD|=\frac{5}{2},
|AB|=4,
|AD|=2 i
|BC|=\frac{3}{2}.
Ramiona trapezu przedłużono
do przecięcia w punkcie O.
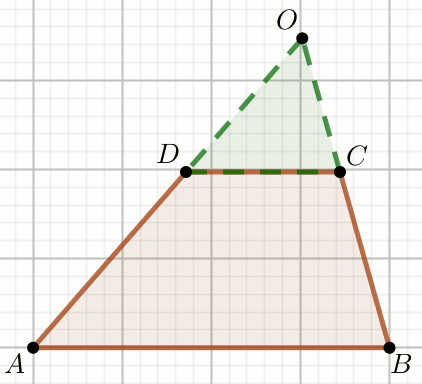
Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.

Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.
Odpowiedź:
| L_{\triangle ABC}= | |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20722 |
Podpunkt 15.1 (2 pkt)
» Trójkąt na rysunku jest równoramienny o podstawie
AB:
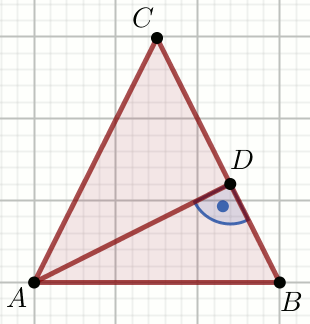

Oblicz |AB|.
Dane
|CD|=\frac{14}{5}=2.800000000000
|DB|=\frac{36}{5}=7.20000000000000
|DB|=\frac{36}{5}=7.20000000000000
Odpowiedź:
| |AB|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20743 |
Podpunkt 16.1 (2 pkt)
«« Kąt \alpha jest kątem ostrym oraz zachodzi
równość a\cos^2\alpha+b\sin^2\alpha=c.
Wyznacz wartość wyrażenia (\tan\alpha+\cot\alpha)^2.
Dane
a=3
b=7
c=6
b=7
c=6
Odpowiedź:
| (\tan\alpha+\cot\alpha)^2= | |
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20058 |
Podpunkt 17.1 (2 pkt)
O liczbie naturalnej n wiadomo, że
5|n,
100\leqslant n\leqslant 999,
n jest nieparzysta, a suma cyfry setek i cyfry
dziesiątek wynosi s.
W liczbie n wymieniono miejscami cyfry dziesiątek
i jedności i wówczas otrzymano liczbę o k większą.
Wyznacz n.
Dane
s=4
k=27
k=27
Odpowiedź:
n=
(wpisz liczbę całkowitą)
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20881 |
Podpunkt 18.1 (2 pkt)
W trójkącie równoramiennym ABC podstawa AB
ma długość 8, a wysokość CD ma
taką samą długośc jak odcinek łączący punkt D ze środkiem boku
BC.
Oblicz długość wysokości CD.
Odpowiedź:
| |CD|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20007 |
Podpunkt 19.1 (1 pkt)
Rozwiąż równanie
\left|a-\left|x+b\right|\right|=c
.
Podaj najmniejsze z rozwiązań tego równania.
Dane
a=-1
b=-6
c=3
b=-6
c=3
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 19.2 (1 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-21115 |
Podpunkt 20.1 (2 pkt)
Rozwiąż równanie
|4x-24|=2|3x-13|
.
Podaj najmniejsze i największe rozwiązanie tego równania.
Odpowiedzi:
| min | = |
(wpisz liczbę zapisaną dziesiętnie) |
| max | = |
(wpisz liczbę zapisaną dziesiętnie) |