Podgląd arkusza : lo2@am-2-2022-10-09-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10216 |
Podpunkt 1.1 (1 pkt)
Ustal dla ilu liczb całkowitych wyrażenie
\frac{18}{n-5} jest liczbą całkowitą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10298 |
Podpunkt 2.1 (1 pkt)
Jeżelia=\log_{9}{2}-\log_{9}{18} i
b=-\frac{1}{2}\log_{3}{243}, to:
Odpowiedzi:
| A. b > a | B. a-b=0 |
| C. a > b | D. a+b=0 |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10742 |
Podpunkt 3.1 (1 pkt)
« Ile miejsc zerowych ma funkcja
f(x)=
\begin{cases}
x-6\text{, dla } x\in(-\infty, 0\rangle \\
1+7x^2\text{, dla } x\in(0,+\infty)
\end{cases}
?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11503 |
Podpunkt 4.1 (1 pkt)
Funkcje liniowe określone wzorami f(x)=\frac{1}{3}x-5 oraz
g(x)=mx+2 mają wspólne miejsce zerowe.
Wyznacz m.
Odpowiedź:
| m= | |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11116 |
Podpunkt 5.1 (1 pkt)
Do wykresu funkcji określonej wzorem f(x)=\frac{a}{x}, dla
x\neq 0 należy punkt o współrzędnych
A=(7,-6).
Podaj wartość parametru a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11462 |
Podpunkt 6.1 (1 pkt)
Trójkąt o bokach długości \sqrt{2}+1,
\sqrt{2}+1, 2+\sqrt{3}, jest:
Odpowiedzi:
| A. jest ostrokątny | B. jest prostokątny |
| C. jest rozwartokątny | D. nie istnieje |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10581 |
Podpunkt 7.1 (1 pkt)
Odcinki AM i
CN są wysokościami trójkąta
ABC.
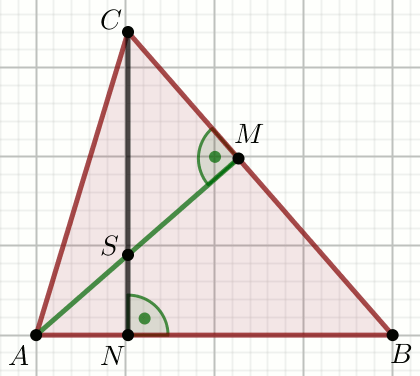

Zatem:
Odpowiedzi:
| A. |\sphericalangle BAM|=|\sphericalangle BCN| | B. |\sphericalangle CAM|=|\sphericalangle ACN| |
| C. |\sphericalangle BSN|=|\sphericalangle CAM| | D. |\sphericalangle BAM|=|\sphericalangle ASN| |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11538 |
Podpunkt 8.1 (1 pkt)
Kąt \alpha jest ostry i spełnia warunek
\sin\alpha=\frac{3}{4}.
Oblicz wartość wyrażenia \sin^2\alpha-\cos^2\alpha.
Odpowiedź:
| \sin^2\alpha-\cos^2\alpha= | |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10788 |
Podpunkt 9.1 (1 pkt)
« Na rysunkach przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
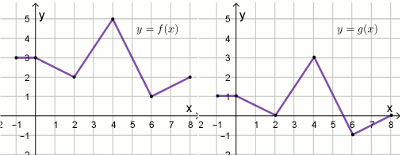
Funkcja f określona jest wzorem:

Odpowiedzi:
| A. f(x)=g(x-2) | B. f(x)=g(x+2) |
| C. f(x)=g(x)-2 | D. f(x)=g(x)+2 |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11709 |
Podpunkt 10.1 (1 pkt)
Wyznacz najmniejsze rozwiązanie równania
\frac{|x+9\sqrt{3}|-2}{\sqrt{3}}=4
i zapisz wynik w najprostszej postaci a+b\sqrt{c}.
Odpowiedź:
x_{min}=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20082 |
Podpunkt 11.1 (2 pkt)
Rozwiąż równanie z niewiadomą x:
\frac{2x-3}{x+3}=\frac{4x}{2x+7}
.
Odpowiedź:
| x= | |
| Zadanie 12. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30049 |
Podpunkt 12.1 (2 pkt)
« Rozwiąż nierówność\frac{(x-1)^2}{3}+\frac{15}{2}<=\frac{16}{9}x-\frac{1-x}{2}\cdot \left(\frac{2}{3}x+3\right).
Podaj najmniejszą liczbe spęłniającą tę nierówność.
Odpowiedź:
| min= | |
Podpunkt 12.2 (2 pkt)
Najmniejszą liczbę spęłniającą tę nierówność zapisz w postaci ułamka
nieskracalnego o dodatnim mianowniku.
Podaj mianownik tego ułamka.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20325 |
Podpunkt 13.1 (2 pkt)
» Rozwiąż układ równań
\begin{cases}
3x+2y=3 \\
y+2=\frac{3(1-x)+4}{2}
\end{cases}
.
Punkt A=(10, m) należy do rozwiązania. Podaj m.
Odpowiedź:
| \frac{p}{q}= | |
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21025 |
Podpunkt 14.1 (2 pkt)
W trójkącie równoramiennym o obwodzie 200 wysokość opuszczona na
podstawę ma długość 60.
Oblicz długość ramienia tego trójkata.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20249 |
Podpunkt 15.1 (2 pkt)
Na ramieniu kąta ostrego o wierzchołku A zaznaczono
odcinki AB i BC, na
drugim ramieniu odcinki AD i
DE. Odcinki mają długości:
|AB|=4, |BC|=12,
|AD|=6 i |DE|=\frac{14}{3}.
Wyznacz skalę podobieństwa trójkątów ACD i
ABE.
Podaj skalę k\in(0,1].
Odpowiedź:
| k= | |
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21034 |
Podpunkt 16.1 (2 pkt)
Rozwiąż nierówność podwójną 2-|2x-8|\leqslant 2|-8+2x|\leqslant 4.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy i największy z końców liczbowych tych przedziałów.
Odpowiedzi:
| min | = |
(wpisz liczbę zapisaną dziesiętnie) |
| max | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20569 |
Podpunkt 17.1 (2 pkt)
» Wyznacz dziedzinę funkcji:
f(x)=\frac{x+6}{ax^3+bx^2+cx+d}
Podaj sumę tych wszystkich wartości x, które nie należą do dziedziny tej funkcji.
Dane
a=27
b=-54
c=36
d=-8
b=-54
c=36
d=-8
Odpowiedź:
| suma= | |
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20027 |
Podpunkt 18.1 (2 pkt)
Przeciwprostokątna trójkąta prostokątnego ma długość
c, a jedna z przyprostokątnych jest o
d dłuższa od drugiej.
Oblicz obwód tego trójkąta.
Dane
c=593
d=97
d=97
Odpowiedź:
L=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20948 |
Podpunkt 19.1 (2 pkt)
Rozwiąż równanie
\frac{6|x+14|-\left(\left|-x-14\right|+4\sqrt{5}\right)}{3}-4=|x+14|-2\sqrt{5}
.
Najmniejsze z rozwiązań zapisz w najprostszej postaci a+b\sqrt{c},
gdzie a,b,c\in\mathbb{Z}.
Odpowiedź:
Wpisz odpowiedź:
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20905 |
Podpunkt 20.1 (1 pkt)
Rozwiąż równanie
|3x+15|+14=2|5x+25|
.
Podaj najmniejsze rozwiązanie tego równania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 20.2 (1 pkt)
Podaj największe rozwiązanie tego równania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)