Podgląd arkusza : lo2@am-2-2022-11-06-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11586 |
Podpunkt 1.1 (1 pkt)
Która równość jest prawdziwa:
Odpowiedzi:
| A. 49^3=(-49)^3 | B. -49^2=(-49)^2 |
| C. \sqrt{(-49)^2}=-49 | D. -\sqrt[3]{49}=\sqrt[3]{-49} |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10723 |
Podpunkt 2.1 (1 pkt)
Do wykresu funkcji f(x)=(m-1)x+m^2-15 należy punkt
P=(0,10).
Wyznacz wartość parametru m.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10874 |
Podpunkt 3.1 (1 pkt)
Rozwiązaniem układu równań
\begin{cases}
5x+7y=\frac{29}{2} \\
4x-7y=-1
\end{cases}
jest para liczb:
Odpowiedzi:
| A. x=\frac{1}{2}\wedge y=\frac{3}{2} | B. x=\frac{3}{2}\wedge y=1 |
| C. x=\frac{5}{2}\wedge y=1 | D. x=\frac{3}{2}\wedge y=2 |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10308 |
Podpunkt 4.1 (1 pkt)
Przedstawiony na rysunku wykres może być wykresem funkcji:
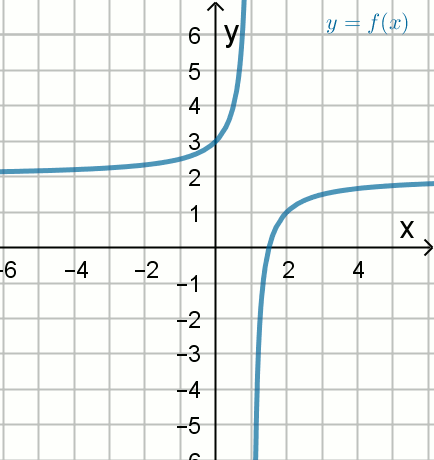

Odpowiedzi:
| A. f(x)=-\frac{2}{x-1}-2 | B. f(x)=2-\frac{2}{x+1} |
| C. f(x)=2-\frac{2}{x-1} | D. f(x)=2+\frac{2}{x+1} |
| E. f(x)=1-\frac{2}{x+2} | F. f(x)=-\frac{2}{x-2}-1 |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-11596 |
Podpunkt 5.1 (1 pkt)
Wektory
\vec{u}=[2m+n-9, m-3n-21]
oraz
\vec{v}=[m, -n+8] są równe.
Wyznacz wartości parametrów m i n
Odpowiedzi:
| m | = |
(wpisz liczbę zapisaną dziesiętnie) |
| n | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10674 |
Podpunkt 6.1 (1 pkt)
« Przekątna równoległoboku o kącie ostrym \alpha o mierze
60^{\circ} i wysokości o długości
28\sqrt{3}, tworzy kąt prosty z jego bokiem.
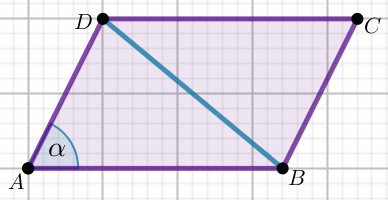

Oblicz obwód tego równoległoboku.
Odpowiedź:
L=
(wpisz liczbę całkowitą)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11613 |
Podpunkt 7.1 (1 pkt)
Oblicz wartość wyrażenia |x+7|-|x+8|, gdzie
x\in(-\infty,-10).
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11427 |
Podpunkt 8.1 (1 pkt)
Funkcja kwadratowa jest określona wzorem
f(x)=-(-2x-8)(x-3). Liczby
x_1 i x_2 są różnymi
miejscami zerowymi funkcji f spełniającymi warunek
x_1+x_2=..........
Podaj brakującą liczbę.
Odpowiedzi:
| A. x_1+x_2=-1 | B. x_1+x_2=1 |
| C. x_1+x_2=-2 | D. x_1+x_2=2 |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11470 |
Podpunkt 9.1 (1 pkt)
» Przesuwając wykres funkcji określonej wzorem
h(x)=x^2-8 o k=3 jednostek
w prawo otrzymamy wykres funkcji opisanej wzorem y=x^2+bx+c.
Wyznacz współczynniki b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 10. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20028 |
Podpunkt 10.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
2(x-3)-(4-3x) > 3x-10
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| x_L= | |
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20305 |
Podpunkt 11.1 (2 pkt)
Miara kąta wewnętrznego wielokąta foremnego jest równa
171 stopnie.
Ile wierzchołków ma ten wielokąt?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20486 |
Podpunkt 12.1 (2 pkt)
Do wykresu funkcji f(x)=-\frac{9}{x}+q należy punkt
\left(\frac{9}{2},\frac{7}{2}\right).
Wyznacz q.
Odpowiedź:
| q= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20236 |
Podpunkt 13.1 (2 pkt)
« Jedna z przyprostokątnych trójkąta prostokątnego ma długość
20, a wysokość opuszczona na przeciwprostokątną
tego trójkata długość 10\sqrt{3}.
Oblicz długość drugiej przyprostokątnej tego trójkąta.
Odpowiedź:
b=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20277 |
Podpunkt 14.1 (2 pkt)
» Kąt ostry \alpha spełnia równanie
\sin\alpha+\cos\alpha=\frac{\sqrt{7}}{2}.
Oblicz (\sin\alpha-\cos\alpha)^2
Odpowiedź:
| (\sin\alpha-\cos\alpha)^2= | |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20368 |
Podpunkt 15.1 (1 pkt)
» Wyznacz najmniejszą wartość funkcji
g(x)=ax^2+bx+c w przedziale
\langle p,q\rangle.
Dane
a=1
b=-4
c=6
p=-3
q=1
b=-4
c=6
p=-3
q=1
Odpowiedź:
f_{min}(x)=
(wpisz liczbę całkowitą)
Podpunkt 15.2 (1 pkt)
Wyznacz największą wartość tej funkcji w podanym przedziale.
Odpowiedź:
f_{max}(x)=
(wpisz liczbę całkowitą)
| Zadanie 16. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30002 |
Podpunkt 16.1 (2 pkt)
« Wyznacz te wartości całkowite x, dla których liczba
\frac{(9x^2-a)(x+1)}{3x^3+bx^2-3x-b} jest całkowita.
Podaj najmniejsze z rozwiązań.
Dane
a=121
b=11
b=11
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 16.2 (2 pkt)
Podaj największe z rozwiązań.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20881 |
Podpunkt 17.1 (2 pkt)
W trójkącie równoramiennym ABC podstawa AB
ma długość 28, a wysokość CD ma
taką samą długośc jak odcinek łączący punkt D ze środkiem boku
BC.
Oblicz długość wysokości CD.
Odpowiedź:
| |CD|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-21117 |
Podpunkt 18.1 (1 pkt)
« Rozwiąż równanie
|2x+7|-\sqrt{4x^2+46x+151}=0
.
Podaj najmniejsze rozwiązanie tego równania.
Odpowiedź:
| x_{min}= | |
Podpunkt 18.2 (1 pkt)
Podaj największe rozwiązanie tego równania.
Odpowiedź:
| x_{max}= | |
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20459 |
Podpunkt 19.1 (2 pkt)
« Dla jakiej wartości parametru m zbiorem wartości
funkcji liczbowej g(x)=x^2+3x+m-8 jest przedział
\langle -2,+\infty).
Odpowiedź:
| m= | |