Podgląd arkusza : lo2@am-2-2022-11-13-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10080 |
Podpunkt 1.1 (1 pkt)
» Zbiorem rozwiązań nierówności
\sqrt{-x} \lessdot -3
jest:
Odpowiedzi:
| A. (-\infty,3\rangle | B. \emptyset |
| C. (3,+\infty) | D. (-\infty,-3\rangle |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10427 |
Podpunkt 2.1 (1 pkt)
Największą z liczb
a=-16^{-\frac{1}{4}},
b=\left(-\sqrt[4]{\frac{1}{16}}\right)^{-1},
c=-\sqrt[5]{3^{10}},
d=-\frac{5^{\frac{1}{5}}}{5^{-\frac{4}{5}}}
jest:
Odpowiedzi:
| A. c | B. d |
| C. b | D. a |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10754 |
Podpunkt 3.1 (1 pkt)
Punkt M o rzędnej równej 6
należy do wykresu funkcji f(x)=2+\frac{4}{1-x}.
Wyznacz odciętą punktu M.
Odpowiedź:
| x_M= | |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10883 |
Podpunkt 4.1 (1 pkt)
« Proste p i q są
równoległe, a punkt O(0,0) leży pomiędzy nimi.
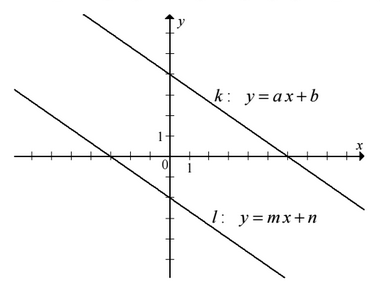

Zatem:
Odpowiedzi:
| A. a\cdot m \lessdot 0 \ \wedge\ b\cdot n < 0 | B. a\cdot m > 0 \ \wedge\ b\cdot n \lessdot 0 |
| C. a\cdot m > 0 \ \wedge\ b\cdot n > 0 | D. a\cdot m \lessdot 0 \ \wedge\ b\cdot n > 0 |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10849 |
Podpunkt 5.1 (1 pkt)
» Rozwiązaniem układu równań:
\begin{cases}
7x+10y=-58 \\
-x-3y=13
\end{cases}
jest para liczb (x_0,y_0).
Podaj liczby x_0 i y_0.
Odpowiedzi:
| x_0 | = |
(wpisz liczbę całkowitą) |
| y_0 | = |
(wpisz liczbę całkowitą) |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11569 |
Podpunkt 6.1 (1 pkt)
Równanie x\cdot y=5 spełniają tylko dwie takie pary liczb,
w których obie liczby są naturalne.
Ile par liczb całkowitych spełnia równanie x\cdot y=18?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10588 |
Podpunkt 7.1 (1 pkt)
«« Prostokąt ABCD o przekątnej długości
4\sqrt{13} jest podobny do prostokąta o bokach
długości 2 i 3.
Oblicz obwód prostokąta ABCD.
Odpowiedź:
| L= | |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10622 |
Podpunkt 8.1 (1 pkt)
Kąt \alpha należy do przedziału
(90^{\circ},180^{\circ}) i zachodzi równość
\cos\alpha=-\frac{1}{4}.
Oblicz \tan\alpha.
Odpowiedź:
\tan\alpha=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11609 |
Podpunkt 9.1 (1 pkt)
Zbiorem wartości funkcji f jest przedział \langle -5,10\rangle.
Zbiorem wartości funkcji określonej wzorem g(x)=f(x+7)+2 jest przedział
\langle c,d\rangle.
Podaj liczby c i d.
Odpowiedzi:
| c | = |
(wpisz liczbę zapisaną dziesiętnie) |
| d | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11559 |
Podpunkt 10.1 (1 pkt)
Równanie |x-3|+5=0:
Odpowiedzi:
| A. ma dokładnie dwa rozwiązania | B. nie ma rozwiązań |
| C. ma więcej niż dwa rozwiązania | D. ma dokładnie jedno rozwiązanie |
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20116 |
Podpunkt 11.1 (2 pkt)
» Rozwiąż równanie
\frac{2x-6}{x\sqrt{3}}=-\frac{1}{6}
o niewiadomej x.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20153 |
Podpunkt 12.1 (1 pkt)
Rozwiąż równanie z niewiadomą x:
4x^2+3x=0
.
Podaj najmniejsze z rozwiązań tego równania.
Odpowiedź:
| x_{min}= | |
Podpunkt 12.2 (1 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
| x_{max}= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20146 |
Podpunkt 13.1 (2 pkt)
Oblicz
w=\frac{a^{-2}-3\cdot \left(\frac{a}{3}\right)^{-2}}
{5-\left(\frac{1}{a}\right)^{-1}}
.
Dane
a=3
Odpowiedź:
| w= | |
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20295 |
Podpunkt 14.1 (2 pkt)
» Dana jest funkcja
f(x)=
\begin{cases}
2x+1\text{, dla } x\leqslant 0 \\
x+2\text{, dla } x > 0
\end{cases}
Podaj sumę wszystkich miejsc zerowych tej funkcji.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20299 |
Podpunkt 15.1 (2 pkt)
Suma cyfr liczby dwucyfrowej jest równa 11.
Jeśli zamienimy miejscami cyfry w tej liczbie, to otrzymamy liczbę o
9 większą.
Wyznacz tę liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21023 |
Podpunkt 16.1 (1 pkt)
«Wyznacz wartości parametrów a i b,
dla których rozwiązaniem układu równań
\begin{cases}
(a+2b-6)x-(b+1)y=6 \\
5x-(a+b-7)y=2a-16
\end{cases}
jest para liczb (2,2).
Podaj a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 16.2 (1 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20244 |
Podpunkt 17.1 (1 pkt)
W trójkącie prostokątnym najkrótszy bok ma długość \frac{3}{2}, a
najdłuższy bok jest dłuższy od dłuższej przyprostokątnej o \frac{1}{2}.
Oblicz długość dłuższej przyprostokątnej tego trójkąta.
Odpowiedź:
| max= | |
Podpunkt 17.2 (1 pkt)
Oblicz odległość punktu przecięcia się środkowych tego trójkąta od
wierzchołka kąta prostego.
Odpowiedź:
| d= | |
| Zadanie 18. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30021 |
Podpunkt 18.1 (4 pkt)
« W trójkąt prostokątny wpisano okrąg, który jest styczny do
przeciwprostokątnej w punkcie M.
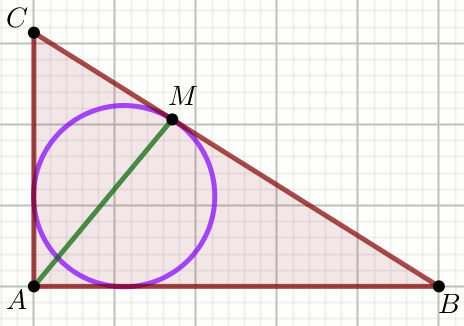

Oblicz |AM|.
Dane
|AC|=3
|AB|=4
|AB|=4
Odpowiedź:
| |AM|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20296 |
Podpunkt 19.1 (1 pkt)
» Dana jest funkcja f(x)=\frac{759}{x}, gdzie
x\neq 0. Jej wykres przesunięto wzdłuż osi
Oy i otrzymano wykres funkcji
y=g(x), do którego należy punkt
B=(23,52). Wyznacz wektor tego przesunięcia
\vec{u}=[u_x,u_y].
Podaj u_y.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 19.2 (1 pkt)
Ile liczb naturalnych k ze zbioru
\{0,1,2,3,...,195\} ma tę własność, że liczba
g(k) jest całkowita?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21034 |
Podpunkt 20.1 (2 pkt)
Rozwiąż nierówność podwójną 2-|2x-11|\leqslant 2|-11+2x|\leqslant 4.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy i największy z końców liczbowych tych przedziałów.
Odpowiedzi:
| min | = |
(wpisz liczbę zapisaną dziesiętnie) |
| max | = |
(wpisz liczbę zapisaną dziesiętnie) |