Podgląd arkusza : lo2@am-2-2022-11-13-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10072 |
Podpunkt 1.1 (1 pkt)
Dane są dwie sumy algebraiczne
4x^2-2x-6 oraz
4x^3-2x^2+6x. Iloczyn tych sum jest równy
16x^5+mx^4+nx^3-36x.
Podaj liczby m i n.
Odpowiedzi:
| m | = |
(wpisz liczbę całkowitą) |
| n | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10692 |
Podpunkt 2.1 (1 pkt)
Dziedziną funkcji f określonej wzorem
f(x)=\log{(x^2+100)}
jest zbiór:
Odpowiedzi:
| A. (-10;10) | B. (-\infty;-10)\cup(10;+\infty) |
| C. \mathbb{R}-\{-10;10\} | D. \mathbb{R} |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11702 |
Podpunkt 3.1 (0.5 pkt)
Rozwiąż układ równań metodą przeciwnych współczynników:
\begin{cases}
1,2x-\frac{2}{5}y=\frac{92}{5} \\
\frac{2}{3}y+0,2x=\frac{101}{15}
\end{cases}
Podaj x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 3.2 (0.5 pkt)
Podaj y.
Odpowiedź:
y=
(wpisz liczbę całkowitą)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11630 |
Podpunkt 4.1 (1 pkt)
Funkcja kwadratowa określona jest wzorem
f(x)=-2x^2+24x-69,
a wierzchołek jej wykresu ma współrzędne W=(x_w,y_w).
Wyznacz współrzędne wierzchołka W.
Odpowiedzi:
| x_w | = |
(wpisz liczbę całkowitą) |
| y_w | = |
(wpisz liczbę całkowitą) |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10580 |
Podpunkt 5.1 (1 pkt)
« Oblicz obwód trójkąta równobocznego o polu powierzchni równym 44\sqrt{3}.
Odpowiedź:
m\sqrt{n}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10649 |
Podpunkt 6.1 (1 pkt)
« W trójkącie prostokątnym najdłuższy bok ma długość
26, a najkrótszy 10.
Oblicz tangens największego kąta ostrego tego trójkąta.
Odpowiedź:
| \tan\alpha= | |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10396 |
Podpunkt 7.1 (1 pkt)
Zbiór rozwiązań nierówności 5x-m+\frac{9}{2}\lessdot 0
jest przedziałem (-\infty, 4).
Podaj wartość parametru m.
Odpowiedź:
| m= | |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10980 |
Podpunkt 8.1 (1 pkt)
Liczby -2 i \frac{11}{2} są miejscami
zerowymi funkcji określonej wzorem g(x)=ax^2-\frac{21}{2}x-33.
Wyznacz wartość współczynnika a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11062 |
Podpunkt 9.1 (1 pkt)
Na rysunku pokazano cześć wykresu funkcji
g(x)=ax^2+bc+c.
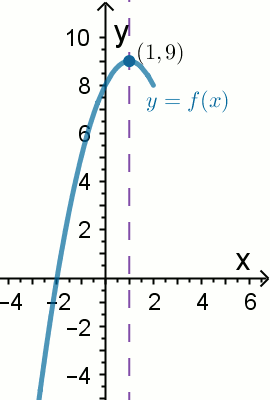

Które z poniższych zdań jest prawdziwe?
Odpowiedzi:
| A. miejsca zerowe tej funkcji to -2 i 4 | B. miejscami zerowymi funkcji to -2 i 6 |
| C. f(x) > 0 \iff x \lessdot 1 | D. funkcja rośnie w przedziale (-2,4) |
| Zadanie 10. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20179 |
Podpunkt 10.1 (1 pkt)
Rozwiąż równanie z niewiadomą x:
(x-5)(x-3)-4x-4=0
.
Podaj najmniejsze z rozwiązań tego równania.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 10.2 (1 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20306 |
Podpunkt 11.1 (1 pkt)
« Dane są punkty A=(-7, 107) i
B=(-4, 65). Wyznacz równanie prostej
AB.
Podaj współczynnik kierunkowy tej prostej.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 11.2 (1 pkt)
Wyznacz odciętą punktu przecięcia prostej AB
z osią Ox.
Odpowiedź:
| x_0= | |
| Zadanie 12. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30397 |
Podpunkt 12.1 (4 pkt)
Odległość między dwoma miastami
wynosi 89 km. Pociąg pokonuję tę trasę ze średnią
prędkością v. Gdyby pociąg jechał o
14 km/h szybciej, to do miasta docelowego
przyjechałby o 32 minut szybciej. Gdyby zaś pociąg jechał
o 26 km/h wolniej, to pokonywałby tę trasę o
208 minut dłużej.
Z jaką średnią prędkością pociąg zwyczajowo pokonuję tę trasę?
Odpowiedź:
v[km/h]=
(wpisz liczbę całkowitą)
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20779 |
Podpunkt 13.1 (1 pkt)
« W trójkącie ABC dane są:
A=(8,0), B=(-1,-1)
i C=(3,-5). Oblicz długości boków tego trójkąta.
Podaj długość boku najkrótszego.
Odpowiedź:
min=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 13.2 (1 pkt)
Podaj długość boku najdłuższego.
Odpowiedź:
max=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20274 |
Podpunkt 14.1 (2 pkt)
Kąt \alpha jest ostry. Oblicz wartość wyrażenia
2+\sin^3\alpha+\sin\alpha\cdot \cos^2\alpha.
Dane
\cos\alpha=\frac{\sqrt{7}}{4}=0.66143782776615
Odpowiedź:
| Wpisz odpowiedź: |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20336 |
Podpunkt 15.1 (1 pkt)
» Punkt P=(5,0) jest wierzchołkiem paraboli określonej
równaniem y=2x^2+4px+q-2.
Oblicz wartości współczynników p i
q.
Podaj wartość p.
Odpowiedź:
p=
(wpisz liczbę całkowitą)
Podpunkt 15.2 (1 pkt)
Podaj wartość q.
Odpowiedź:
q=
(wpisz liczbę całkowitą)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20017 |
Podpunkt 16.1 (2 pkt)
Wiadomo, że \log_{a}{4}=x oraz
\log_{b}{4}=y.
Oblicz \log_{ab}{4}.
Dane
x=10
y=\frac{1}{5}=0.20000000000000
y=\frac{1}{5}=0.20000000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20026 |
Podpunkt 17.1 (2 pkt)
« Zielony czworokąt na rysunku jest wpisany w trójkąt równoramienny
o podstawie długości a i jest prostokątem:
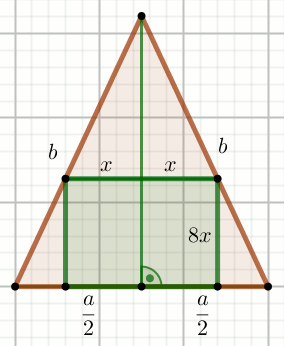

Oblicz jego obwód.
Dane
a=80
b=58
b=58
Odpowiedź:
| L= | |
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-21137 |
Podpunkt 18.1 (2 pkt)
Wyznacz zbiór tych wszystkich wartości parametru p\in\mathb{R},
dla których rozwiązaniem nierówności
(2+p)x-|p+3|+8\geqslant 0 jest przedział (-\infty, -5\rangle.
Podaj najmniejsze możliwe p.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 19. (3 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20839 |
Podpunkt 19.1 (1 pkt)
» Dana jest funkcja
f(x)=x^2-(m+1)x+\frac{5}{2}m+\frac{1}{4}. Funkcja
h liczbie m
przyporządkowuje najmniejszą wartość funkcji f w
przedziale \langle -1,1\rangle. Wyznacz
wzór tej funkcji.
Podaj h(a\sqrt{5}).
Dane
a=-5
b=4
b=4
Odpowiedź:
| h(a\sqrt{5})= |
|
|
| (wpisz cztery liczby całkowite) | ||
Podpunkt 19.2 (1 pkt)
Podaj długość przedziału, w którym funkcja ta określona jest wzorem
h(m)=-\frac{1}{4}m^2+2m.
Odpowiedź:
d=
(wpisz liczbę całkowitą)
Podpunkt 19.3 (1 pkt)
Podaj h\left(\frac{b}{2}\right).
Odpowiedź:
| h\left(\frac{b}{2}\right)= | |