Podgląd arkusza : lo2@am-2-2022-11-20-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10009 |
Podpunkt 1.1 (1 pkt)
» Różnica zbiorów
\langle -10,10\rangle - (-7,-3\rangle jest równa:
Odpowiedzi:
| A. \langle -10,-7\rangle\cup(-3,10\rangle | B. \langle -10,-7)\cup(-3,10) |
| C. \langle -10,-7)\cup\langle-3,10\rangle | D. \langle -10,-7)\cap\langle-3,10\rangle |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10317 |
Podpunkt 2.1 (1 pkt)
Prawdziwa jest równość:
Odpowiedzi:
| A. \left(-\frac{5}{6}\right)^{-1}=\frac{6}{5} | B. \log_{\frac{1}{5}}{125}=-3 |
| C. \log_{5}{4}=625 | D. 2\log{100}+\log{0.01}=4 |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10754 |
Podpunkt 3.1 (1 pkt)
Punkt M o rzędnej równej 4
należy do wykresu funkcji f(x)=2+\frac{4}{1-x}.
Wyznacz odciętą punktu M.
Odpowiedź:
| x_M= | |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10817 |
Podpunkt 4.1 (1 pkt)
« Dane są funkcje f(x)=-2x-3 oraz
g(x)=f(x+4)+2. Zapisz wzór funkcji g
w postaci g(x)=ax+b.
Podaj współczynniki a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10954 |
Podpunkt 5.1 (1 pkt)
Pierwsza rata, która stanowi 18\% ceny roweru
szosowego, jest o 545 zł niższa od raty drugiej,
która stanowi 20\% ceny roweru.
Ile złotych kosztuje rower?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11628 |
Podpunkt 6.1 (1 pkt)
Wyznacz miejsca zerowe funkcji określonej wzorem
f(x)=-4(x-2)^2+100.
Odpowiedzi:
| x_{min} | = |
(wpisz liczbę całkowitą) |
| x_{max} | = |
(wpisz liczbę całkowitą) |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10584 |
Podpunkt 7.1 (1 pkt)
Przedstawione na rysunku trójkąty ABC i
PQR są podobne.

Oblicz długość boku AB trójkąta ABC.

Odpowiedź:
| |AB|= | |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10622 |
Podpunkt 8.1 (1 pkt)
Kąt \alpha należy do przedziału
(90^{\circ},180^{\circ}) i zachodzi równość
\cos\alpha=-\frac{1}{2}.
Oblicz \tan\alpha.
Odpowiedź:
\tan\alpha=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11704 |
Podpunkt 9.1 (0.5 pkt)
Równanie o niewiadomej x postaci |x-a|-b=0
ma dwa rozwiązania 4 i -1.
Podaj liczbę a.
Odpowiedź:
| a= | |
Podpunkt 9.2 (0.5 pkt)
Podaj liczbę b.
Odpowiedź:
| b= | |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11084 |
Podpunkt 10.1 (1 pkt)
Dana jest funkcja y=x^2-2.
Do zbioru ZW_f nie należy liczba:
Odpowiedzi:
| A. 6-2\sqrt{10} | B. 2-2\sqrt{6} |
| C. 5-2\sqrt{6} | D. 7-4\sqrt{3} |
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20073 |
Podpunkt 11.1 (2 pkt)
Rozwiąż równanie z niewiadomą x:
\frac{x-3}{-8-x}=\frac{1}{2}
.
Odpowiedź:
| x= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20182 |
Podpunkt 12.1 (1 pkt)
Rozwiąż równanie z niewiadomą x:
x^3+13x^2-16x-208=0
.
Podaj najmniejsze z rozwiązań tego równania.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 12.2 (1 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20955 |
Podpunkt 13.1 (2 pkt)
Średni wiek zawodnika n osobowej drużyny piłkarskiej jest równy 28 lat.
Trener tej drużyny ma 60 lat, a średni wiek zawodników drużyny wraz z trenerem
jest równy 30 lat.
Wyznacz liczbę n.
Odpowiedź:
n=
(wpisz liczbę całkowitą)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20295 |
Podpunkt 14.1 (2 pkt)
» Dana jest funkcja
f(x)=
\begin{cases}
2x+1\text{, dla } x\leqslant 0 \\
x+2\text{, dla } x > 0
\end{cases}
Podaj sumę wszystkich miejsc zerowych tej funkcji.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20845 |
Podpunkt 15.1 (2 pkt)
« Liczba b spełnia równanie
(b+2-\sqrt{2})^2-(b+2-2\sqrt{2})^2=-6.
Podaj miejsce zerowe funkcji określonej wzorem f(x)=-10x+b.
Odpowiedź:
| x= | |
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20486 |
Podpunkt 16.1 (2 pkt)
Do wykresu funkcji f(x)=-\frac{9}{x}+q należy punkt
\left(\frac{9}{2},-\frac{9}{2}\right).
Wyznacz q.
Odpowiedź:
| q= | |
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20877 |
Podpunkt 17.1 (2 pkt)
Trzy liczby 2x+13, x+10 i
4x+15 są długościami boków trójkąta równoramiennego.
Wyznacz najmniejszy możliwy L_{min} i największy możliwy L_{max} obwód tego trójkąta.
Odpowiedzi:
| L_{min} | = |
(wpisz liczbę całkowitą) |
| L_{max} | = |
(wpisz liczbę całkowitą) |
| Zadanie 18. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30135 |
Podpunkt 18.1 (4 pkt)
« Punkt E jest środkiem przeciwprostokątnej
AB trójkąta ABC.
Odcinek DE ma długość 1, jak na rysunku.
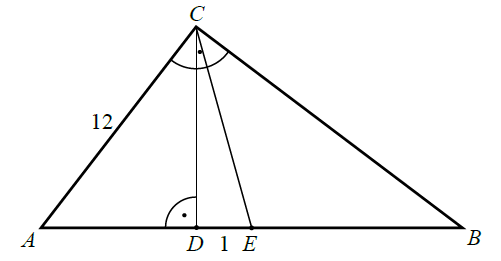
Oblicz obwód trójkąta ABC.
Odpowiedź:
L_{\triangle ABC}=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20264 |
Podpunkt 19.1 (2 pkt)
Oblicz wartość wyrażenia
\frac{a\sin\alpha+b\cos\alpha}
{b\cos\alpha+c\sin\alpha}
,
jeśli wiadomo, że \alpha jest kątem ostrym
oraz \tan\alpha=m.
Dane
a=6
b=-3
c=1
m=6
b=-3
c=1
m=6
Odpowiedź:
| \frac{p}{q}= | |
| Zadanie 20. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30086 |
Podpunkt 20.1 (2 pkt)
Pan Nowak ma d metrów bieżących siatki i zamierza
ogrodzić ogródek w kształcie prostokąta o możliwie największej powierzchni,
przy czym na jednym z boków tego prostokąta musi zostawić
4 m na bramę wjazdową. Jakie wymiary powinien mieć
prostokątny ogródek, aby jego pole powierzchni było jak największe?
Podaj krótszy bok tego prostokąta.
Dane
d=36
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 20.2 (2 pkt)
Podaj pole powierzchni tego prostokąta.
Odpowiedź:
P=
(wpisz liczbę całkowitą)