Podgląd arkusza : lo2@am-2-2022-11-27-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10098 |
Podpunkt 1.1 (1 pkt)
» Liczby a i c są dodatnie.
Liczba b stanowi 52\%
liczby a oraz 25\%
liczby c.
Wynika stąd, że:
Odpowiedzi:
| A. c=0.48\cdot a | B. c=2.08\cdot a |
| C. c=2.18\cdot a | D. c=0.21\cdot a |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10702 |
Podpunkt 2.1 (1 pkt)
Funkcja f określona jest wzorem
f(x)=\frac{2x^3}{x^4+2} dla każdej liczby rzeczywistej
x.
Zapisz liczbę f\left(-\sqrt{3}\right) w najprostszej nieskracalnej
postaci \frac{a\sqrt{b}}{c}, gdzie a\in\mathbb{Z} i
b,c\in\mathbb{N}.
Odpowiedź:
| Wpisz odpowiedź: | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10852 |
Podpunkt 3.1 (1 pkt)
« Dana jest prosta o równaniu k:4x-2y+2=0. Prosta
k tworzy z prostą lukład
sprzeczny.
Prosta l może być opisana równaniem:
Odpowiedzi:
| A. l:y-2x=-1 | B. l:-2x-4y+2=0 |
| C. l:4x+2y+2=0 | D. l:2x-y=-1 |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11117 |
Podpunkt 4.1 (1 pkt)
Dla której z podanych wartości a, wykres funkcji określonej wzorem
f(x)=\frac{a}{x} nie ma punktów wspólnych z wykresem
prostej o równaniu y=9x:
Odpowiedzi:
| A. a=\frac{1}{4} | B. a=\sqrt{4} |
| C. a=5 | D. a=2 |
| E. a=-\sqrt{5} | F. a=3 |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11394 |
Podpunkt 5.1 (0.5 pkt)
Dany jest punkt B=(3,-4) oraz wektor
\overrightarrow{AB}=[1, -3]. Wyznacz środek odcinka S_{AB}=(x_S, y_S).
Podaj x_S.
Odpowiedź:
| x_S= | |
Podpunkt 5.2 (0.5 pkt)
Podaj y_S.
Odpowiedź:
| y_S= | |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10646 |
Podpunkt 6.1 (1 pkt)
« Na płaszczyźnie dane są punkty
A=\left(12\sqrt{5},12\sqrt{15}\right),
B=\left(0,0\right) i
C=\left(12\sqrt{5},0\right).
Kąt CBA ma miarę:
Odpowiedzi:
| A. 30^{\circ} | B. 60^{\circ} |
| C. 45^{\circ} | D. 75^{\circ} |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11706 |
Podpunkt 7.1 (0.5 pkt)
Równanie o niewiadomej x postaci |x+a|-b=0
ma dwa rozwiązania 2 i 6.
Podaj liczbę a.
Odpowiedź:
| a= | |
Podpunkt 7.2 (0.5 pkt)
Podaj liczbę b.
Odpowiedź:
| b= | |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10979 |
Podpunkt 8.1 (1 pkt)
Dana jest funkcja f określona wzorem f(x)=-8(x+1)^2-5.
Wyznacz największą wartość funkcji określonej wzorem h(x)=f(x-3)+3.
Odpowiedź:
h_{max}(x)=
(wpisz liczbę całkowitą)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11046 |
Podpunkt 9.1 (1 pkt)
Wskaż wykres mający 3 punkty wspólne z osiami
układu współrzędnych:
Odpowiedzi:
| A. y=-5x^2+3x-6 | B. y=-4(x-1)^2+12 |
| C. y=-5x^2-4x-4 | D. y=3x^2+2x+5 |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10112 |
Podpunkt 10.1 (1 pkt)
Funkcja h(x)=x^2+5x+c ma dwa miejsca zerowe, gdy:
Odpowiedzi:
| A. c=12 | B. c=14 |
| C. c=9 | D. c=13 |
| E. c=11 | F. c=4 |
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20104 |
Podpunkt 11.1 (2 pkt)
Rozwiąż równanie
\frac{x+3}{3}-2(x-2)=\frac{x}{3}-x
o niewiadomej x.
Odpowiedź:
| x= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20840 |
Podpunkt 12.1 (1 pkt)
« Funkcja liniowa f określona wzorem
f(x)=mx+n wartości nieujemne przyjmuje tylko
w przedziale (-\infty, 5\rangle oraz zachodzi
warunek f(-4)=9. Wyznacz wartości współczynników
m i n.
Podaj m.
Odpowiedź:
| m= | |
Podpunkt 12.2 (1 pkt)
Podaj n.
Odpowiedź:
| n= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20326 |
Podpunkt 13.1 (1 pkt)
» Kinga jest o 8 lat starsza od Kamila.
5 lat temu Kamil był dwa razy młodszy pod Kingi.
Ile lat ma teraz Kamil.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 13.2 (1 pkt)
Ile lat ma teraz Kinga.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20917 |
Podpunkt 14.1 (2 pkt)
» Trójkąt ABC jest prostokątny.
Na boku AC tego trójkąta zbudowano kwadrat,
natomiast bok AB przedłużono tak, że
|\angle EHA|=90^{\circ}.
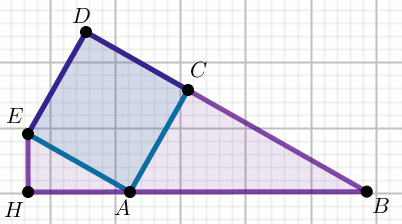

Wiedząc, że |BC|=36 oraz bok kwadratu ma długość 27 oblicz pole powierzchni trójkąta EHA.
Odpowiedź:
| P_{\triangle EHA}= | |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20740 |
Podpunkt 15.1 (1 pkt)
« Dany jest trójkąt:
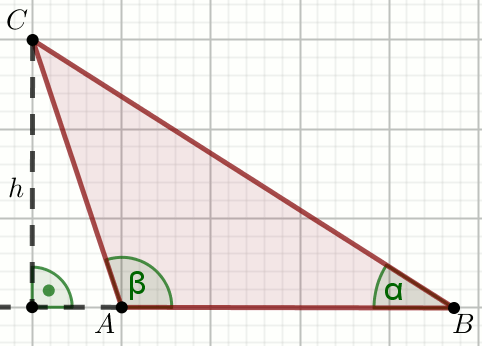

Oblicz |AC|. Do obliczeń użyj przybliżeń wartości funkcji trygonometrycznych z dokładnością do dwóch miejsc po przecinku.
Dane
\alpha=48^{\circ}
\beta=98^{\circ}
h=14
\beta=98^{\circ}
h=14
Odpowiedź:
| |AC|= | |
Podpunkt 15.2 (1 pkt)
Oblicz |AB|. Do obliczeń użyj przybliżeń wartości
funkcji trygonometrycznych z dokładnością do dwóch miejsc po przecinku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 16. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30075 |
Podpunkt 16.1 (2 pkt)
Dane sa wykresy funkcji f i
g. Funkcja f jest
określona wzorem f(x)=-2x^2+20x-32, a mniejsze z
jej miejsc zerowych jest jednocześnie miejscem zerowym funkcji
g. Wierzchołek W paraboli,
która jest wykresem funkcji f, leży na wykresie
funkcji g, a wierzchołek Z
paraboli będącej wykresem funkcji g leży na osi
Oy układu współrzędnych.
Wyznacz wzór funkcji g(x)=ax^2+bx+c.
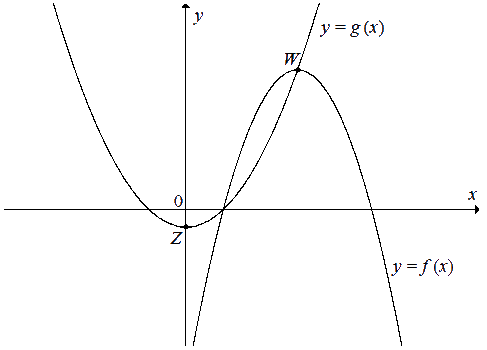
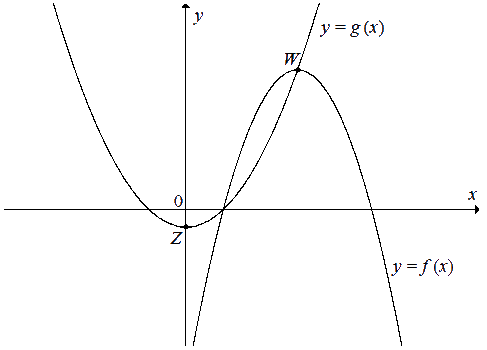
Podaj liczbę a.
Odpowiedź:
| a= | |
Podpunkt 16.2 (2 pkt)
Podaj liczbę c.
Odpowiedź:
| c= | |
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20943 |
Podpunkt 17.1 (2 pkt)
Boki trójkąta mają długości 5x+y+18,
3x+y+10 i 4y-2x-16,
a jego obwód ma długość 18. Wyznacz wszystkie pary liczb całkowitych,
które spełniają warunki zadania.
Podaj liczby x i y tej pary, która ma największą rzędną.
Odpowiedzi:
| x | = |
(wpisz liczbę całkowitą) |
| y | = |
(wpisz liczbę całkowitą) |
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20026 |
Podpunkt 18.1 (2 pkt)
« Zielony czworokąt na rysunku jest wpisany w trójkąt równoramienny
o podstawie długości a i jest prostokątem:
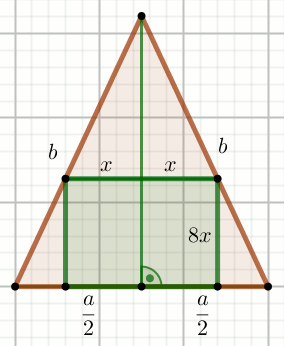

Oblicz jego obwód.
Dane
a=54
b=45
b=45
Odpowiedź:
| L= | |
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20043 |
Podpunkt 19.1 (1 pkt)
« Rozwiąż równanie |x+3+a|+|a+x-1|=x+18+a.
Podaj najmniejsze z rozwiązań.
Dane
a=2
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 19.2 (1 pkt)
Podaj największe z rozwiązań.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 20. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30089 |
Podpunkt 20.1 (4 pkt)
«« Funkcja liniowa określona jest wzorem y=x-p.
Na wykresie tej funkcji znajdź taki punkt o współrzędnych
P=(a,b), aby suma
a^2+b^2 miała najmniejszą możliwą wartość.
Podaj tę najmniejszą możliwą sumę.
Dane
p=8
Odpowiedź:
| min\left(a^2+b^2\right)= | |