Podgląd arkusza : lo2@am-2-2022-12-04-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11585 |
Podpunkt 1.1 (1 pkt)
Oblicz wartość wyrażenia
\log_{0,1}{10000}-\log_{0,1}{10000000}
.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10706 |
Podpunkt 2.1 (1 pkt)
Liczba -1 jest miejscem zerowym
funkcji f(x)=(2m-1)x+3.
Wyznacz wartość parametru m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10919 |
Podpunkt 3.1 (1 pkt)
Funkcja f jest liniowa oraz
f(-4)=3 i f(-3)=1.
Oblicz f(0).
Odpowiedź:
f(0)=
(wpisz liczbę całkowitą)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11725 |
Podpunkt 4.1 (1 pkt)
Do wykresu funkcji logarytmicznej określonej wzorem
f(x)=\log_{a}{x} należy punkt
P=\left(\frac{1}{243},5\right).
Oblicz podstawę logarytmu a.
Odpowiedź:
| a= | |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10596 |
Podpunkt 5.1 (1 pkt)
« Odcinki DE i AB
są równoległe, przy czym
|DE|=\frac{1}{3} i
|AB|=1:
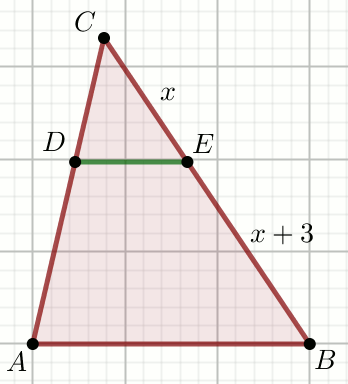

Oblicz x.
Odpowiedź:
| x= | |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10638 |
Podpunkt 6.1 (1 pkt)
Kąt \alpha jest kątem ostrym w trójkącie prostokątnym.
Przeciwprostokątna tego trójkąta ma długość 16, a
\cos\alpha=\frac{1}{8}.
Wynika z tego, że:
Odpowiedzi:
| A. \sin\alpha=\frac{7}{8} | B. przeciwprostokątna tego trójkąta jest dwa razy dłuższa od przyprostokątnej |
| C. jedna z przyprostokątnych jest 8 razy krótsza od przeciwprostokątnej | D. przyprostokatna tego trójkąta ma długość 1 |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-11601 |
Podpunkt 7.1 (1 pkt)
Dane jest wyrażenie \sqrt{4x^2-4x+1}-2\sqrt{(x+1)^2}+3|x+3|,
gdzie x\in(-\infty,-3). Zapisz to wyrażenie w postaci
ax+b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11009 |
Podpunkt 8.1 (0.2 pkt)
« Maksymalny zbiór, w którym funkcja kwadratowa
f(x)=-5(x+8)^2+6 jest rosnąca jest pewnym przedziałem liczbowym.
Przedział ten ma postać:
Odpowiedzi:
| A. (-\infty,p) | B. \langle p,q\rangle |
| C. (-\infty,p\rangle | D. (p,+\infty) |
| E. (p,q) | F. \langle p,+\infty) |
Podpunkt 8.2 (0.8 pkt)
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11451 |
Podpunkt 9.1 (1 pkt)
Wykres funkcji określonej wzorem f(x)=x^2-4
przesunięto o k=6 jednostek w prawo. W wyniku
tego przesunięcia otrzymano wykres funkcji określonej wzorem
y=x^2+bx+c.
Wyznacz współczynniki b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11645 |
Podpunkt 10.1 (1 pkt)
« Rzucono pionowo do góry kamień z prędkością początkową 10\ m/s.
Wysokość s\ [m], jaką osiągnie ten kamień po t
sekundach czasu opisuje wzór s(t)=12t-6t^2.
Podaj maksymalną wysokość jaką osiągnie ten kamień.
Odpowiedź:
s_{max}(t)=
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20138 |
Podpunkt 11.1 (2 pkt)
Oblicz średnią arytmetyczną liczb \log_{a}{b},
-\log_{a}{c} i 2.
Dane
a=3
b=52488
c=8
b=52488
c=8
Odpowiedź:
| s= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20299 |
Podpunkt 12.1 (2 pkt)
Suma cyfr liczby dwucyfrowej jest równa 15.
Jeśli zamienimy miejscami cyfry w tej liczbie, to otrzymamy liczbę o
27 większą.
Wyznacz tę liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20879 |
Podpunkt 13.1 (1 pkt)
Samochód osobowy jadący ze średnią prędkością 60 km/h
pokonuje pewną drogę w czasie 3 godzin i 12 minut. W jakim czasie pokona tę drogę motorowerzysta jadący ze średnią prekością
36 km/h?
Wynik podaj w minutach.
Odpowiedź:
t[min]=
(wpisz liczbę całkowitą)
Podpunkt 13.2 (1 pkt)
Z jaką prędkością należy jechać, aby pokonać tę drogę w czasie
4 godzin i 48 minut?
Wynik podaj w kilometrach na godzinę.
Odpowiedź:
v[km/h]=
(wpisz liczbę całkowitą)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20868 |
Podpunkt 14.1 (1 pkt)
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego dzieli
przeciwprostokątną na dwa odcinki, z których jeden jest o 8 krótszy od tej wysokości,
a drugi o 16 od niej dłuższy.
Oblicz długość przeciwprostokątnej tego trójkąta.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
Podpunkt 14.2 (1 pkt)
Oblicz długość najkrótszej wysokości tego trójkąta.
Odpowiedź:
h=
(wpisz liczbę całkowitą)
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20734 |
Podpunkt 15.1 (1 pkt)
Kąt \alpha jest ostry. Oblicz \cos\alpha.
Dane
\sin\alpha=\frac{16}{65}=0.24615384615385
Odpowiedź:
| \cos\alpha= | |
Podpunkt 15.2 (1 pkt)
Oblicz \tan\alpha.
Odpowiedź:
| \tan\alpha= | |
| Zadanie 16. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30081 |
Podpunkt 16.1 (4 pkt)
« Dana jest funkcja kwadratowa
h(x)=-\frac{1}{2}x^2-x+7,5 określona w przedziale
w przedziale \langle -2, m+a\rangle. Funkcja
h spełnia warunek
h_{max}-h_{min}=\frac{9}{2}.
Oblicz m.
Dane
a=6
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20001 |
Podpunkt 17.1 (1 pkt)
Dane są zbiory: A=(a,b),
B=\langle c,d\rangle,
C=(-\infty,e\rangle. Wyznacz zbiór
(A\cap B)-C.
Ile liczb całkowitych zawiera ten zbiór?
Dane
a=-3
b=9
c=-9
d=10
e=0
b=9
c=-9
d=10
e=0
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 17.2 (1 pkt)
Ile jest równa suma tych liczb całkowitych?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 18. (3 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-21198 |
Podpunkt 18.1 (1 pkt)
Dany jest trójkąt równoramienny ABC, w którym
|AC|=|AB|=39, a punkt D jest środkiem podstawy
AB. Okrąg o środku D jest styczny do prostej
AC w punkcie M. Punkt K
leży na boku AC, punkt L leży na boku
BC, odcinek KL jest styczny do rozważanego okręgu
oraz |KC|=|LC|=3 (zobacz rysunek).
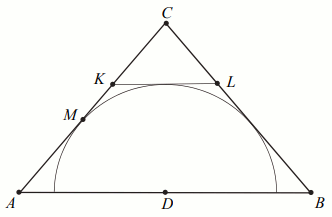

Oblicz |KL|.
Odpowiedź:
| |KL|= | |
Podpunkt 18.2 (2 pkt)
Oblicz \frac{|AM|}{|MC|}.
Odpowiedź:
| |AM|:|MC|= | |
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20041 |
Podpunkt 19.1 (1 pkt)
Rozwiąż nierówność
|2x+4|+|x-1| > 5
.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
| min= | |
Podpunkt 19.2 (1 pkt)
Podaj największy z końców liczbowych tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20067 |
Podpunkt 20.1 (1 pkt)
« Dla jakich wartości parametru m najmniejsza
wartość funkcji
g(x)=x^2+x+m^2-(2a+1)m+a^2+a+\frac{1}{4}
należy do przedziału \langle 2,6\rangle?
Podaj najmniejsze takie m.
Dane
a=1
Odpowiedź:
m_{min}=
(wpisz liczbę całkowitą)
Podpunkt 20.2 (1 pkt)
Podaj największe takie m.
Odpowiedź:
m_{max}=
(wpisz liczbę całkowitą)