Podgląd arkusza : lo2@am-2-2023-01-22-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10431 |
Podpunkt 1.1 (1 pkt)
Oblicz wartość wyrażenia
\frac{2^{10}\cdot 3^{9}\cdot 7^{10}}{21^{9}\cdot 2^{5}}
.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10276 |
Podpunkt 2.1 (1 pkt)
Które z poniższych wzorów opisują funkcję malejącą?
Odpowiedzi:
| T/N : f(x)=-2\sqrt{x-3}-1 | T/N : f(x)=\sqrt{x+3} |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10884 |
Podpunkt 3.1 (1 pkt)
Funkcja liniowa f określona jest wzorem
f(x)=2^{28}x-2^{25}.
Prosta będąca wykresem funkcji f nie przechodzi przez ćwiartkę układu:
Odpowiedzi:
| A. drugą | B. pierwszą |
| C. czwartą | D. trzecią |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11626 |
Podpunkt 4.1 (0.2 pkt)
Funkcja kwadratowa określona jest wzorem
f(x)=3x^2-6x+2.
Zbiorem wartości tej funkcji jest przedział postaci:
Odpowiedzi:
| A. \langle p,+\infty) | B. (p,+\infty) |
| C. (-\infty, p\rangle | D. (-\infty, p) |
Podpunkt 4.2 (0.8 pkt)
Podaj koniec liczbowy tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10602 |
Podpunkt 5.1 (1 pkt)
Zielone odcinki na rysunku sa równolegle, przy czym
|AP|=\frac{1}{2},
|BP|=\frac{3}{4},
|CP|=\frac{3}{2},
|DP|=1,
|AB|=\frac{3}{2}:
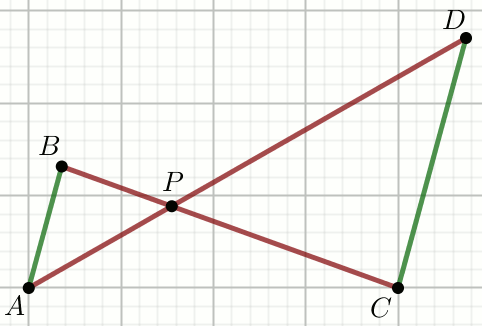

Oblicz długość odcinka CD.
Odpowiedź:
| |CD|= | |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10638 |
Podpunkt 6.1 (1 pkt)
Kąt \alpha jest kątem ostrym w trójkącie prostokątnym.
Przeciwprostokątna tego trójkąta ma długość 8, a
\cos\alpha=\frac{1}{4}.
Wynika z tego, że:
Odpowiedzi:
| A. \sin\alpha=\frac{3}{4} | B. przyprostokatna tego trójkąta ma długość 1 |
| C. jedna z przyprostokątnych jest 4 razy krótsza od przeciwprostokątnej | D. przeciwprostokątna tego trójkąta jest dwa razy dłuższa od przyprostokątnej |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10788 |
Podpunkt 7.1 (1 pkt)
« Na rysunkach przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
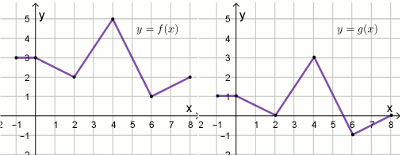
Funkcja g określona jest wzorem:

Odpowiedzi:
| A. g(x)=f(x+2) | B. g(x)=f(x)+2 |
| C. g(x)=f(x-2) | D. g(x)=f(x)-2 |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10983 |
Podpunkt 8.1 (1 pkt)
Wierzchołek paraboli y=x^2-4x leży na prostej
o równaniu:
Odpowiedzi:
| A. y=-4x | B. y=-1x |
| C. y=2x | D. y=1x |
| E. y=4x | F. y=-2x |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10966 |
Podpunkt 9.1 (1 pkt)
« Zbiorem wartości funkcji
y=-(x-3)(x+3)
określonej dla x\in(1,4\rangle jest pewien przedział liczbowy,
którego lewy koniec jest równy p, a prawy koniec jest równy
q.
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11466 |
Podpunkt 10.1 (1 pkt)
« Dana jest funkcja kwadratowa
f(x)=-0,5(x+2m)^2+6m, gdzie
m > 0.
Wówczas:
Odpowiedzi:
| A. dla m=-\frac{1}{2} funkcja jest rosnąca | B. wierzchołek paraboli, która jest wykresem tej funkcji należy do prostej y=-3x |
| C. największą wartością funkcji jest -6m | D. dla pewnego m funkcja ma jedno miejsce zerowe |
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20065 |
Podpunkt 11.1 (2 pkt)
Stosunek dwóch liczb różniących się o 43
jest równy \frac{5}{9}.
Podaj większą z tych liczb.
Odpowiedź:
| max= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20839 |
Podpunkt 12.1 (2 pkt)
« Prosta k jest równoległa do prostej
AB wyznaczonej przez punkty punkty
A=(1,-5) i B=(-2,4)
i przecina oś Oy w punkcie o rzędnej równej
2. Dla jakiej wartości parametru
k punkt C=(-2k-18, 5k+50)
należy do prostej k?
Podaj k.
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20723 |
Podpunkt 13.1 (2 pkt)
« Dane są punkty na okręgu
takie, że |AP|=\frac{9}{4},
|PB|=3 i
|CP|=\frac{9}{4}:
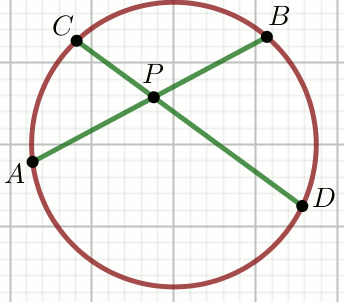

Oblicz |PD|.
Odpowiedź:
| |PD|= | |
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20735 |
Podpunkt 14.1 (1 pkt)
« Kąt \alpha spełnia warunek:
\alpha\in(90^{\circ},180^{\circ}).
Oblicz \sin\alpha.
Dane
\tan\alpha=-\frac{28}{45}=-0.62222222222222
Odpowiedź:
| \sin\alpha= | |
Podpunkt 14.2 (1 pkt)
Oblicz \cos\alpha.
Odpowiedź:
| \cos\alpha= | |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20860 |
Podpunkt 15.1 (1 pkt)
Rozwiąż nierówność 2(x-7)(x-9)+3x-21 > 3(x-8)+1.
Podaj najmniejszą liczbę, która nie spełnia tej nierówności.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 15.2 (1 pkt)
Podaj największą liczbę, która nie spełnia tej nierówności.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20941 |
Podpunkt 16.1 (1 pkt)
« Wyznacz wszystkie pary liczb całkowitych
x i y,
które spełniają równość
(2x-y+a)(x-y+b)=c.
Ile jest takich par?
Dane
a=-4
b=-1
c=31
b=-1
c=31
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 16.2 (1 pkt)
Podaj największą z rzędnych wszystkich rozwiązań.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20973 |
Podpunkt 17.1 (2 pkt)
Wyznacz wszystkie wartości parametru m\in\mathbb{R}, dla których
wykresy funkcji liniowych f(x)=2x-m+10 oraz
g(x)=-4x+5m-14 przecinają się w punkcie o współrzędnych
(x,y) takim, że
|y|\geqslant |x|+5.
Podaj najmniejszą możliwą wartość parametru m.
Odpowiedź:
| m_{min}= | |
| Zadanie 18. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30082 |
Podpunkt 18.1 (2 pkt)
Rozwiąż nierówność
\left|x^2+(a+6)x+\frac{a^2}{4}+3a-1\right| \leqslant 6
.
Rozwiązaniem tej nierówności jest zbiór \langle x_1, x_2\rangle\cup\langle x_3, x_4\rangle\, gdzie x_2\lessdot x_3. Podaj x_1+x_2.
Dane
a=1
Odpowiedź:
x_1+x_2=
(wpisz liczbę całkowitą)
Podpunkt 18.2 (2 pkt)
Podaj x_3.
Odpowiedź:
| x_{3}= | |
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20458 |
Podpunkt 19.1 (2 pkt)
« Liczby x_1 i x_2
są miejscami zerowymi funkcji kwadratowej. Liczby te są względem siebie
odwrotne i spełniają warunek x_1+x_2=m, przy czym
x_1 \lessdot x_2.
Podaj x_1.
Dane
m=-7
Odpowiedź:
| x_{1}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20095 |
Podpunkt 20.1 (1 pkt)
Wyznacz wartości parametru m, dla których dziedziną
funkcji f(x)=\sqrt{(m-8)x^2+x(m-8)+1} jest
zbiór \mathbb{R}.
Podaj najmniejsze takie m.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 20.2 (1 pkt)
Podaj największe takie m.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)