Podgląd arkusza : lo2@am-2-2023-03-19-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10300 |
Podpunkt 1.1 (1 pkt)
Oblicz wartość wyrażenia w=\log_{4}{\frac{1}{25}}-\log_{4}{\frac{16}{25}}+\log_{0,2}{625}.
Odpowiedź:
w=
(wpisz liczbę całkowitą)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10916 |
Podpunkt 2.1 (1 pkt)
Funkcja liniowa y=ax+b ma ujemne miejsce zerowe, a jej
wykres przecina oś Oy poniżej punktu
(0,0).
Wówczas:
Odpowiedzi:
| A. a \lessdot 0 \wedge b \lessdot 0 | B. a \lessdot 0 \wedge b > 0 |
| C. a > 0 \wedge b \lessdot 0 | D. a > 0 \wedge b > 0 |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10874 |
Podpunkt 3.1 (1 pkt)
Rozwiązaniem układu równań
\begin{cases}
5x-y=\frac{31}{2} \\
-8x+7y=-14
\end{cases}
jest para liczb:
Odpowiedzi:
| A. x=\frac{9}{2}\wedge y=2 | B. x=\frac{7}{2}\wedge y=2 |
| C. x=\frac{5}{2}\wedge y=\frac{5}{2} | D. x=\frac{7}{2}\wedge y=3 |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11723 |
Podpunkt 4.1 (0.5 pkt)
Dane są potęgi \left(\frac{1}{10}\right)^{2},
\left(\frac{1}{10}\right)^{-1},
\left(\frac{1}{10}\right)^{\sqrt{5}},
\left(\frac{1}{10}\right)^{-2},
\left(\frac{1}{10}\right)^{-\sqrt{3}},
\left(\frac{1}{10}\right)^{\frac{\sqrt{3}}{2}} i
\left(\frac{1}{10}\right)^{-\frac{\sqrt{2}}{2}}.
Podaj wykładnik najmniejszej z nich.
Odpowiedź:
| Wpisz odpowiedź: | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 4.2 (0.5 pkt)
Podaj wykładnik największej z nich.
Odpowiedź:
| Wpisz odpowiedź: | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10589 |
Podpunkt 5.1 (1 pkt)
«« Pięciokąt ABCDE jest foremny.
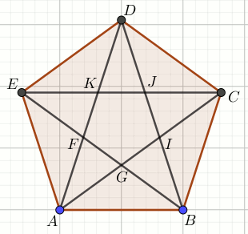

Który z trójkątów nie jest podobny do trójkąta ABD:
Odpowiedzi:
| A. ABG | B. ABI |
| C. BGI | D. EDB |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10632 |
Podpunkt 6.1 (1 pkt)
Kąt \alpha jest ostry i \cos\alpha=\frac{15}{17}.
Oblicz \sin\alpha.
Odpowiedź:
| \sin\alpha= | |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11712 |
Podpunkt 7.1 (1 pkt)
Zapisz wyrażenie |2x+6|-|1-|x+3||, gdzie
x\in(-\infty,-6), w postaci ax+b, gdzie
a,b\in\mathbb{Z}.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10986 |
Podpunkt 8.1 (1 pkt)
Wyznacz przedział o maksymalnej długości, w którym funkcja określona wzorem
h(x)=\frac{1}{2}(x+3)(x-7) jest rosnąca.
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10499 |
Podpunkt 9.1 (1 pkt)
Oblicz miarę stopniową zaznaczonego na rysunku kąta \gamma wiedząc,
że \alpha=33^{\circ} i \beta=57^{\circ}:
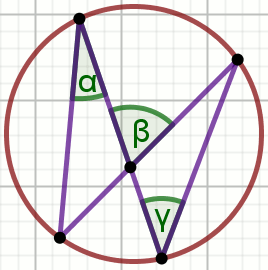 .
.
 .
.
Odpowiedź:
\gamma=
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10559 |
Podpunkt 10.1 (1 pkt)
Pole koła opisanego na trójkącie równobocznym jest równe \frac{1}{3^{11}}\pi^3.
Bok tego trójkąta ma długość \frac{\pi^m}{3^n}, gdzie.
m,n\in\mathbb{Z}.
Podaj liczby m i n.
Odpowiedzi:
| m | = |
(wpisz liczbę całkowitą) |
| n | = |
(wpisz liczbę całkowitą) |
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20002 |
Podpunkt 11.1 (2 pkt)
» Rozwiąż nierówność -\frac{a}{2x}\geqslant 3.
Ile liczb całkowitych spełnia tę nierówność?
Dane
a=48
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20143 |
Podpunkt 12.1 (2 pkt)
Oblicz wartośc wyrażenia
w=\frac{\log_{a}{b}+\log_{a}{1}}{\sqrt{a}\cdot \left(\frac{1}{a^2}\right)^{-2}}
.
Dane
a=3
b=81
b=81
Odpowiedź:
| w= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20772 |
Podpunkt 13.1 (1 pkt)
« Wyznacz dziedzinę funkcji:
f(x)=\frac{2x}{ax+b}+\sqrt{cx+d}
.
Rozwiązanie zapisz w postaci sumy przedziałów. Ile jest tych przedziałów?
Dane
a=3
b=1
c=2
d=2
b=1
c=2
d=2
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 13.2 (1 pkt)
Podaj sumę wszystkich końców liczbowych tych przedziałów.
Odpowiedź:
| \frac{m}{n}= | |
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20305 |
Podpunkt 14.1 (2 pkt)
Miara kąta wewnętrznego wielokąta foremnego jest równa
168 stopnie.
Ile wierzchołków ma ten wielokąt?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20879 |
Podpunkt 15.1 (1 pkt)
Samochód osobowy jadący ze średnią prędkością 70 km/h
pokonuje pewną drogę w czasie 2 godzin i 4 minut. W jakim czasie pokona tę drogę motorowerzysta jadący ze średnią prekością
40 km/h?
Wynik podaj w minutach.
Odpowiedź:
t[min]=
(wpisz liczbę całkowitą)
Podpunkt 15.2 (1 pkt)
Z jaką prędkością należy jechać, aby pokonać tę drogę w czasie
3 godzin i 37 minut?
Wynik podaj w kilometrach na godzinę.
Odpowiedź:
v[km/h]=
(wpisz liczbę całkowitą)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20876 |
Podpunkt 16.1 (1 pkt)
« Trzy liczby x+6, -x i
4x+28 są długościami boków trójkąta, gdy liczba liczba
x należy do przedziału (p,q).
Podaj liczbę p.
Odpowiedź:
| p= | |
Podpunkt 16.2 (1 pkt)
Podaj liczbę q.
Odpowiedź:
| q= | |
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20779 |
Podpunkt 17.1 (1 pkt)
« W trójkącie ABC dane są:
A=(2,6), B=(-7,5)
i C=(-3,1). Oblicz długości boków tego trójkąta.
Podaj długość boku najkrótszego.
Odpowiedź:
min=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 17.2 (1 pkt)
Podaj długość boku najdłuższego.
Odpowiedź:
max=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20781 |
Podpunkt 18.1 (1 pkt)
« Dane są funkcje f oraz
g, przy czym
g(x)=f(x+5)-10. O funkcji f wiadomo, że
f(3)=-6 i f(-2)=15.
Oblicz g(-2).
Odpowiedź:
g(-2)=
(wpisz liczbę całkowitą)
Podpunkt 18.2 (1 pkt)
Podaj wartość argumentu, dla którego funkcja g
przyjmuje wartość 5.
Odpowiedź:
x_0=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20370 |
Podpunkt 19.1 (1 pkt)
» Funkcja kwadratowa f(x)=18x^2+bx+\frac{1}{2} ma tylko
jedno miejsce zerowe. Oblicz b.
Podaj najmniejszą możliwą wartość b.
Odpowiedź:
| b_{min}= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 19.2 (1 pkt)
Odpowiedź:
| b_{max}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 20. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30300 |
Podpunkt 20.1 (2 pkt)
« Spodek wysokości opuszczonej z wierzchołka kąta prostego trójkata prostokatnego
leży w odległości d od środka okręgu opisanego na tym
trójkącie, a wysokość ta ma długość h.
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Dane
d=\frac{21}{2}=10.50000000000000
h=36
h=36
Odpowiedź:
| R= | |
Podpunkt 20.2 (2 pkt)
Oblicz długość obwodu tego trójkąta.
Odpowiedź:
L=
(liczba zapisana dziesiętnie)