Podgląd arkusza : lo2@am-2-2023-04-23-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10432 |
Podpunkt 1.1 (1 pkt)
Zapisz wyrażenie
3^{16}+9^{6}-3^{12}+9^{13}-3^{26}+9^{8}+3^{16}
w postaci potęgi o podstawie 3.
Podaj wykładnik tej potęgi.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10864 |
Podpunkt 2.1 (1 pkt)
» Układ równań
\begin{cases}
-\frac{2}{3}x+\frac{3}{2}y=2 \\
-x+7y=-2
\end{cases}
:
Odpowiedzi:
| A. jest oznaczony | B. jest nieoznaczony |
| C. ma dwa rozwiązania | D. jest sprzeczny |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10475 |
Podpunkt 3.1 (1 pkt)
Proste k i l są równoległe.
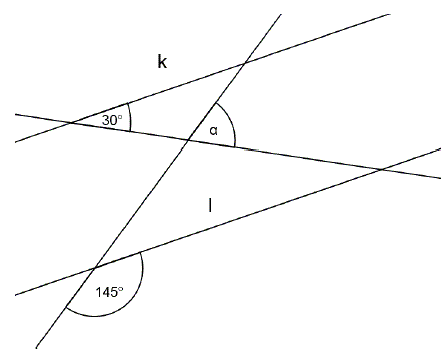

Podaj miarę stopniową kąta \alpha.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10633 |
Podpunkt 4.1 (1 pkt)
« Oblicz wartość wyrażenia
\log{\tan 35^{\circ}}+\log{\tan 45^{\circ}}+\log{\tan 55^{\circ}}
.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10182 |
Podpunkt 5.1 (1 pkt)
Oblicz wartość wyrażenia \frac{|1-12|}{-2}.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11506 |
Podpunkt 6.1 (1 pkt)
Osią symetrii paraboli będącej wykresem funkcji kwadratowej określonej równaniem
f(x)=-\frac{1}{2}(x-48)(x+336), jest prosta określona:
równaniem x-......=0.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10531 |
Podpunkt 7.1 (1 pkt)
Punkt O jest środkiem okręgu, przy czym
\alpha=12^{\circ}:
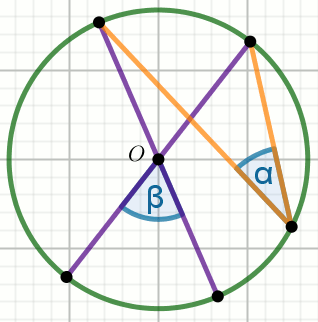

Wyznacz miarę stopniową kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10576 |
Podpunkt 8.1 (1 pkt)
» Trójkąt ABC na rysunku jest równoramienny,
a AD jest dwusieczną kąta przy wierzchołku
A, przy czym |\sphericalangle B|=46^{\circ}:
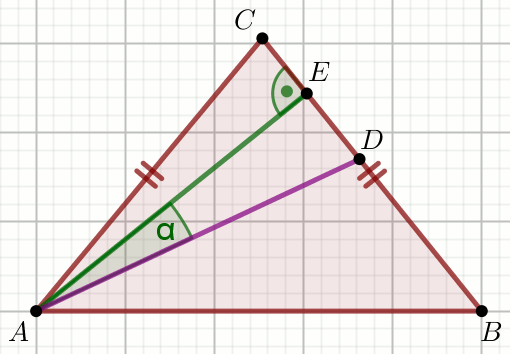

Wyznacz miarę stopniową kąta \alpha.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10895 |
Podpunkt 9.1 (0.5 pkt)
Prosta k o równaniu y=mx+n
tworzy z dodatnią półosią osi Ox kąt o mierze
120^{\circ}. Do prostej
k należy punkt o współrzędnych
(2\sqrt{3},1).
Wyznacz współczynnik m tej prostej.
Odpowiedź:
m=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 9.2 (0.5 pkt)
Wyznacz współczynnik n tej prostej.
Odpowiedź:
n=
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11416 |
Podpunkt 10.1 (1 pkt)
« Do prostej o równaniu y=ax+b należy punkt
A=\left(\frac{1}{2}, 2\right) i prosta ta jest
prostopadła do prostej o równaniu
y=-4x+3.
Wyznacz b.
Odpowiedź:
| b= | |
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20007 |
Podpunkt 11.1 (1 pkt)
Niech A oznacza zbiór liczb naturalnych nieparzystych, mniejszych
od 15, zaś B zbiór
naturalnych dzielników liczby 104. Wyznacz
A\cap B.
Ile elementów zawiera ten zbiór?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (1 pkt)
Ile jest równa suma tych liczb?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20161 |
Podpunkt 12.1 (1 pkt)
Rozwiąż równanie z niewiadomą x:
-4(-2x-5)x=2(-2x-5)
.
Podaj najmniejsze z rozwiązań tego równania.
Odpowiedź:
| x_{min}= | |
Podpunkt 12.2 (1 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
| x_{max}= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20311 |
Podpunkt 13.1 (2 pkt)
« Rozwiąż równanie 2x-2=\sqrt{2}x-5.
Podaj rozwiązanie.
Odpowiedź:
| x= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20837 |
Podpunkt 14.1 (1 pkt)
Rozwiąż układ równań
\begin{cases}
\frac{1}{3}(x-2y)-x=2-\frac{1}{2}(x+2y-2) \\
\frac{1}{2}(x-10)-\frac{1}{4}(2y-12)=x+2y
\end{cases}
.
Podaj x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 14.2 (1 pkt)
Podaj y.
Odpowiedź:
y=
(wpisz liczbę całkowitą)
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20842 |
Podpunkt 15.1 (1 pkt)
Trójkąt ABC ma obwód równy O.
Trójkąt A_1B_1C_1 jest podobny do trójkąta
ABC w skali k. Znając długości
dwóch jego boków oblicz długości boków trójkąta ABC.
Jaką długość ma najkrótszy bok trójkąta ABC?
Dane
O=35
k=5
|A_1B_1|=80
|A_1C_1|=40
k=5
|A_1B_1|=80
|A_1C_1|=40
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 15.2 (1 pkt)
Jaką długość ma najdłuższy bok trójkąta ABC?
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20735 |
Podpunkt 16.1 (1 pkt)
« Kąt \alpha spełnia warunek:
\alpha\in(90^{\circ},180^{\circ}).
Oblicz \sin\alpha.
Dane
\tan\alpha=-\frac{3}{4}=-0.75000000000000
Odpowiedź:
| \sin\alpha= | |
Podpunkt 16.2 (1 pkt)
Oblicz \cos\alpha.
Odpowiedź:
| \cos\alpha= | |
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20402 |
Podpunkt 17.1 (2 pkt)
» Rozwiąż nierówność -x^2+bx+c \lessdot 0.
Ile liczb całkowitych z przedziału \langle 0,100\rangle spełnia tę nierówność?
Dane
b=15
c=-26
c=-26
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
| Zadanie 18. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30015 |
Podpunkt 18.1 (4 pkt)
«« Trójkąt ABC jest prostokątny i jedna z jego
przyprostokątnych jest dwa razy dłuższa od drugiej, a środkowa
CD ma długość d.
Wiedząc, że |\sphericalangle C|=90^{\circ} oblicz promień okręgu wpisanego w ten trójkąt.
Dane
d=2\sqrt{5}=4.472135954999579
Odpowiedź:
| r= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20592 |
Podpunkt 19.1 (1 pkt)
» Punkty A=(3p^2+6p+4, 3-m) oraz
B=(p+2,2m-1) są symetryczne względem osi
Ox.
Podaj m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
Podpunkt 19.2 (1 pkt)
Podaj największe możliwe p.
Odpowiedź:
| p_{max}= | |
| Zadanie 20. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30190 |
Podpunkt 20.1 (2 pkt)
«« Punkt A=(-3,4) jest wierzchołkiem trójkąta
ABC, w którym
\overrightarrow{AB}=[7,3] i
\overrightarrow{BC}=[-6,1].
Wyznacz równanie wysokości tego trójkąta przechodzącej przez punkt
C i zapisz je w postaci
ax+y+c=0.
Podaj a.
Odpowiedź:
| a= | |
Podpunkt 20.2 (2 pkt)
Podaj c.
Odpowiedź:
| c= | |