Podgląd arkusza : lo2@am-3-2022-09-11-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10286 |
Podpunkt 1.1 (1 pkt)
Liczba \log_{6}{9}+\log_{6}{24} jest równa:
Odpowiedzi:
| A. \log_{36}{9} | B. 4 |
| C. 3 | D. \log_{6}{24} |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10891 |
Podpunkt 2.1 (1 pkt)
« Wyznacz zbiór tych wartości parametru m, dla których funkcja liniowa
f(x)=\frac{\left(36-m^2\right)}{4}x-9 jest rosnąca.
Rozwiązanie zapisz w postaci sumy przedziałów.
Najmniejszy z końców liczbowych tych przedziałów jest równy p, a ilość liczb całkowitych należących do rozwiązania jest równa q.
Najmniejszy z końców liczbowych tych przedziałów jest równy p, a ilość liczb całkowitych należących do rozwiązania jest równa q.
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10954 |
Podpunkt 3.1 (1 pkt)
Pierwsza rata, która stanowi 10\% ceny roweru
szosowego, jest o 501 zł niższa od raty drugiej,
która stanowi 14\% ceny roweru.
Ile złotych kosztuje rower?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10605 |
Podpunkt 4.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AD|=\frac{1}{3},
|DE|=\frac{5}{12} i
|AB|=\frac{1}{2}:
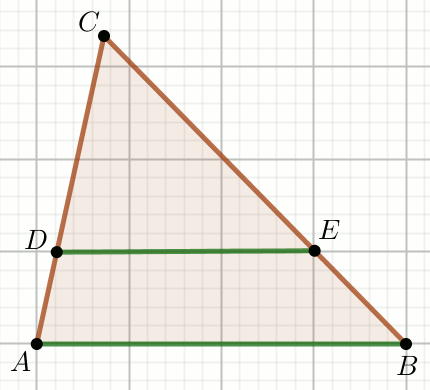

Oblicz długość odcinka DC.
Odpowiedź:
| |DC|= | |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10645 |
Podpunkt 5.1 (1 pkt)
» Dane są długości boków |BC|=7 i
|AC|=4 trójkąta prostokątnego
ABC o kącie ostrym \beta.
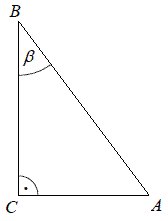

Oblicz x=\sin\beta.
Odpowiedź:
| x= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11575 |
Podpunkt 6.1 (0.5 pkt)
Rozwiąż równanie \left|-3-\frac{3}{8}x\right|-8=0.
Podaj najmniejsze z rozwiązań tego równania.
Odpowiedź:
| x= | |
Podpunkt 6.2 (0.5 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
| x= | |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11506 |
Podpunkt 7.1 (1 pkt)
Osią symetrii paraboli będącej wykresem funkcji kwadratowej określonej równaniem
f(x)=-\frac{1}{2}(x-66)(x+198), jest prosta określona:
równaniem x-......=0.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11687 |
Podpunkt 8.1 (1 pkt)
W trójkąt prostokątny o przyprostokątnych długości 6 i
12 wpisano okrąg. Oblicz długość promienia tego okręgu.
Odpowiedź:
r=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11598 |
Podpunkt 9.1 (1 pkt)
Promień koła ma długość 7, a kąt wycinka tego koła ma miarę
66^{\circ}. Oblicz pole powierzchni tego wycinka i zapisz wynik w postaci
p\cdot\pi.
Podaj liczbę p.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11676 |
Podpunkt 10.1 (1 pkt)
Oblicz wartość wyrażenia algebraicznego
w=(3\sqrt{2}-1)^3.
Odpowiedź:
w=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20087 |
Podpunkt 11.1 (2 pkt)
Suma dwóch liczb jest równa 1419. Jedna z tych liczb
stanowi \frac{16}{17} drugiej.
Podaj większą z tych liczb.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20146 |
Podpunkt 12.1 (2 pkt)
Oblicz
w=\frac{a^{-2}-3\cdot \left(\frac{a}{3}\right)^{-2}}
{5-\left(\frac{1}{a}\right)^{-1}}
.
Dane
a=3
Odpowiedź:
| w= | |
| Zadanie 13. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30046 |
Podpunkt 13.1 (2 pkt)
Dana jest funkcja f(x)=\frac{1}{3}x-7. Naszkicuj jej wykres.
Dla jakich argumentów funkcja ta przyjmuje wartości dodatnie?
Odpowiedź zapisz w postaci sumy przedziałów. Podaj sumę wszystkich końców liczbowych tych przedziałów.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 13.2 (2 pkt)
Rozwiąż nierówność f(1-x)\leqslant 2x+4.
Odpowiedź zapisz w postaci sumy przedziałów. Podaj sumę wszystkich końców liczbowych tych przedziałów.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21023 |
Podpunkt 14.1 (1 pkt)
«Wyznacz wartości parametrów a i b,
dla których rozwiązaniem układu równań
\begin{cases}
(a+2b-13)x-(b-8)y=6 \\
5x-(a+b-5)y=2a+6
\end{cases}
jest para liczb (2,2).
Podaj a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 14.2 (1 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20246 |
Podpunkt 15.1 (2 pkt)
Odcinki AD i BE
przecinają się w punkcie C. W trójkątach
ABC i CDE zachodzą
związki: |\sphericalangle CAB|=|\sphericalangle CED|,
|AC|=5, |BC|=3,
|CE|=10, jak na rysunku.
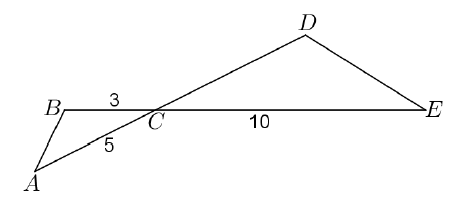

Oblicz długość boku CD.
Odpowiedź:
|CD|=
(wpisz liczbę całkowitą)
| Zadanie 16. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30065 |
Podpunkt 16.1 (2 pkt)
» Punkt O=(0,0) należy do wykresu funkcji
kwadratowej y=g(x). Funkcja
h(x)=g(x+1) przyjmuje wartość największą równą
m dla x=n.
Wyznacz wzory obu funkcji w postaci ogólnej.
Podaj sumę współczynników funkcji g.
Dane
m=5
n=2
n=2
Odpowiedź:
| \frac{a}{b}= | |
Podpunkt 16.2 (2 pkt)
Podaj sumę współczynników h.
Odpowiedź:
| \frac{a}{b}= | |
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20209 |
Podpunkt 17.1 (2 pkt)
« Na trójkącie równoramiennym ABC, w którym
|AC|=|BC| i kąt między ramionami trójkąta ma
miarę \alpha, opisano okrąg o środku w punkcie
S.
Półprosta BS^{\to} przecina bok
AC trójkąta w punkcie K.
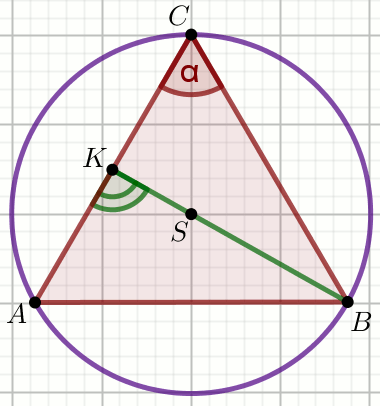

Wyznacz miarę stopniową kąta AKB.
Dane
\alpha=40^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 18. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30189 |
Podpunkt 18.1 (2 pkt)
Okrąg o środku S=(x_S,y_S) przechodzi przez
punkty A=(-1,1),
B=(1,7) i C=(-9,13).
Podaj x_S.
Odpowiedź:
| x_S= | |
Podpunkt 18.2 (2 pkt)
Podaj y_S.
Odpowiedź:
| y_S= | |
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20892 |
Podpunkt 19.1 (2 pkt)
« Dany jest trójkąt, w którym |AB|=12,
|BC|=6\sqrt{2},
|AC|=6+6\sqrt{3} i
\alpha=30^{\circ}:
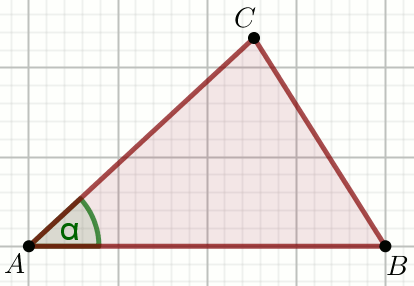

Oblicz miarę stopniową największego kąta tego trójkąta.
Odpowiedź:
\beta_{max}\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20980 |
Podpunkt 20.1 (2 pkt)
Wielomiany W(x)=2ax(2x-b)^2 oraz
P(x)=-16x^3+32x^2-16x
są równe.
Wyznacz liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |