Podgląd arkusza : lo2@am-3-2022-09-18-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10367 |
Podpunkt 1.1 (1 pkt)
Oceń prawdziwość poniższych równości:
Odpowiedzi:
| T/N : 49^3=(-49)^3 | T/N : -49^2=(-49)^2 |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10814 |
Podpunkt 2.1 (1 pkt)
» Na rysunku przedstawiono wykres prostej o równaniu ax+by=4:
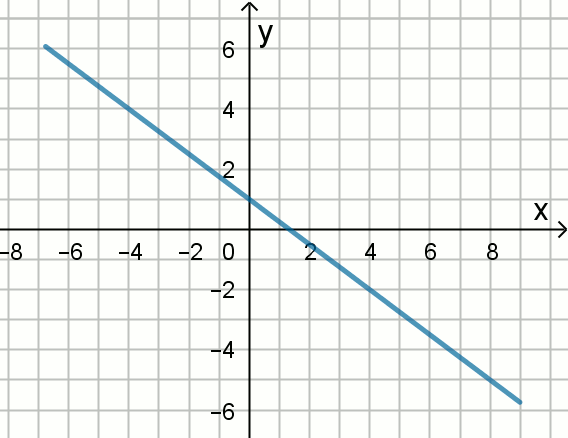

Podaj współczynniki a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10953 |
Podpunkt 3.1 (1 pkt)
« Halę targową budowało n=96 osób przez
297 dni. Teraz taką samą halę trzeba wybudować
w innym mieście w 176 dni.
Ile osób należy zatrudnić?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10578 |
Podpunkt 4.1 (1 pkt)
W trójkącie równoramiennym ABC o wysokościach
CD i AE podstawa
AB ma długość 24,
a odcinek BE ma długość
\frac{72}{5}.
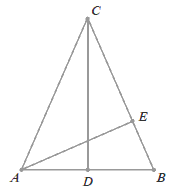

Oblicz długość odcinka CD.
Odpowiedź:
|AC|=
(wpisz liczbę całkowitą)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11743 |
Podpunkt 5.1 (1 pkt)
Wykres funkcji g jest symetryczny do wykresu
funkcji f określonej wzorem
f(x)=-6x^2+8}
względem początku układu współrzędnych.
Zapisz wzór funkcji g w postaci
g(x)=ax^2+b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11709 |
Podpunkt 6.1 (1 pkt)
Wyznacz najmniejsze rozwiązanie równania
\frac{|x+3\sqrt{3}|-2}{\sqrt{3}}=4
i zapisz wynik w najprostszej postaci a+b\sqrt{c}.
Odpowiedź:
x_{min}=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11645 |
Podpunkt 7.1 (1 pkt)
« Rzucono pionowo do góry kamień z prędkością początkową 10\ m/s.
Wysokość s\ [m], jaką osiągnie ten kamień po t
sekundach czasu opisuje wzór s(t)=14t-t^2.
Podaj maksymalną wysokość jaką osiągnie ten kamień.
Odpowiedź:
s_{max}(t)=
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10570 |
Podpunkt 8.1 (1 pkt)
Cięciwa okręgu o promieniu \frac{85}{2} cm ma długość
77 cm.
Oblicz odległość środka okręgu od tej cięciwy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10826 |
Podpunkt 9.1 (1 pkt)
«Proste określone równaniami y=mx+n i -\frac{5}{4}x-\frac{1}{2}y+4=0
są prostopadłe.
Wyznacz m.
Odpowiedź:
| m= | |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11682 |
Podpunkt 10.1 (1 pkt)
« Wielomian określony wzorem P(x)=4x^3-3x^2-4x+1 przy
dzieleniu przez dwumian x-0,5 daje resztę
r.
Wyznacz liczbę r.
Odpowiedź:
| r= | |
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20082 |
Podpunkt 11.1 (2 pkt)
Rozwiąż równanie z niewiadomą x:
\frac{2x-3}{x+3}=\frac{4x}{2x+7}
.
Odpowiedź:
| x= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20182 |
Podpunkt 12.1 (1 pkt)
Rozwiąż równanie z niewiadomą x:
x^3-9x^2-4x+36=0
.
Podaj najmniejsze z rozwiązań tego równania.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 12.2 (1 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20301 |
Podpunkt 13.1 (2 pkt)
Trójkąt ograniczony osiami układu i prostą o równaniu
-4y=4x+8 ma pole powierzchni równe
P.
Oblicz P.
Odpowiedź:
| P_{\triangle}= | |
| Zadanie 14. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30397 |
Podpunkt 14.1 (4 pkt)
Odległość między dwoma miastami
wynosi 125 km. Pociąg pokonuję tę trasę ze średnią
prędkością v. Gdyby pociąg jechał o
6 km/h szybciej, to do miasta docelowego
przyjechałby o 9 minut szybciej. Gdyby zaś pociąg jechał
o 31 km/h wolniej, to pokonywałby tę trasę o
93 minut dłużej.
Z jaką średnią prędkością pociąg zwyczajowo pokonuję tę trasę?
Odpowiedź:
v[km/h]=
(wpisz liczbę całkowitą)
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20255 |
Podpunkt 15.1 (2 pkt)
« Kąt \beta jest ostry. Oblicz wartość wyrażenia
3+2\tan^2\beta.
Dane
\sin\beta=\frac{7}{8}=0.87500000000000
Odpowiedź:
| 3+2\tan^2\beta= | |
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20938 |
Podpunkt 16.1 (1 pkt)
O funkcji kwadratowej określonej wzorem f(x)=ax^2+bx+c wiadomo, że
przyjmuje wartości ujemne wtedy i tylko wtedy, gdy
x\in(-\infty, -8)\cup(-3,+\infty), a do jej wykresu należy punkt
A=(-5,12).
Wyznacz współczynnik a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 16.2 (1 pkt)
Wyznacz współczynniki b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20951 |
Podpunkt 17.1 (2 pkt)
Z punktu P poprowadzono styczną do okręgu
o(O,r). Półprosta PO^{\rightarrow}
przecina ten okrąg w punktach A i B,
przy czym punkt B znajduje się 11
razy dalej od tej stycznej niż punkt A.
Jakim procentem promienia okręgu jest długość odcinka PA?
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20332 |
Podpunkt 18.1 (1 pkt)
Napisz wzór funkcji liniowej y=ax+b, której wykres
przechodzi przez punkt P=(7\sqrt{3},-21) i jest
nachylony do osi Ox pod kątem
150^{\circ}.
Podaj a.
Odpowiedź:
| a= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 18.2 (1 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20756 |
Podpunkt 19.1 (2 pkt)
« Dane są punkty na okręgu:
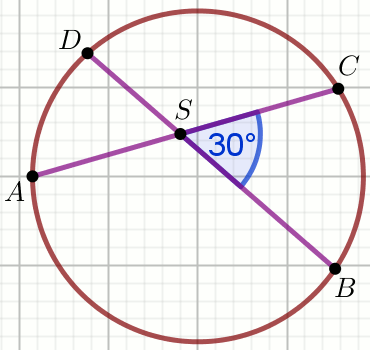

Oblicz P_{\triangle ASD}.
Dane
|AS|=20
|SB|=5
|SC|=12
|SB|=5
|SC|=12
Odpowiedź:
| P_{\triangle ASD}= | |
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21039 |
Podpunkt 20.1 (2 pkt)
«Wielomiany W(x)-F(x), gdzie
W(x)=2x^3+(a-4)x^2+5x-3 i
F(x)=x^3-5x^2+(b+1)x+4, oraz
H(x)=x^3+2x^2+4x-7 są równe.
Wyznacz liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |