Podgląd arkusza : lo2@am-3-2022-10-16-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10414 |
Podpunkt 1.1 (1 pkt)
« Liczbę 4^{20}\cdot 32^{40} można zapiać w postaci:
Odpowiedzi:
| A. 8^{80} | B. 64^{20} |
| C. 4^{100} | D. 2^{200} |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10928 |
Podpunkt 2.1 (1 pkt)
Wykres funkcji liniowej y=\frac{2}{5}x+4 przecina osie
układu współrzędnych w punktach A i
B.
Oblicz pole powierzchni trójkąta AOB.
Odpowiedź:
| P_{AOB}= | |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11632 |
Podpunkt 3.1 (1 pkt)
Zbiorem wartości funkcji określonej wzorem
f(x)=3^x, gdzie x\in(-3,2),
jest przedział (a,b).
Podaj liczby a i b.
Odpowiedzi:
| a | = | (dwie liczby całkowite) | |
| b | = | (dwie liczby całkowite) | |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10580 |
Podpunkt 4.1 (1 pkt)
« Oblicz obwód trójkąta równobocznego o polu powierzchni równym 32\sqrt{3}.
Odpowiedź:
m\sqrt{n}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11748 |
Podpunkt 5.1 (1 pkt)
« W wyniku przekształcenia wykresu funkcji
f(x)=-2\sqrt{x}-3 przez symetrię względem osi
Ox otrzymamo wykres funkcji określonej
wzorem y=a\sqrt{x}+b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11013 |
Podpunkt 6.1 (1 pkt)
Trójmian kwadratowy
y=-2x^2-12x-16 można zapisać w postaci
y=a(x+2)(x-m).
Wyznacz wartości parametrów a i m.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| m | = |
(wpisz liczbę całkowitą) |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10566 |
Podpunkt 7.1 (1 pkt)
« Okręgi o_1(O_1, 4) i
o_2(O_2, 5) są styczne zewnętrznie w punkcie
S, a prosta k
jest styczną do tych okręgów:
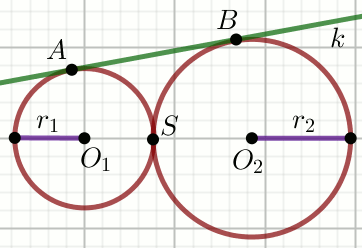

Oblicz długość odcinka AB.
Odpowiedź:
|AB|=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10846 |
Podpunkt 8.1 (1 pkt)
Do prostej o równaniu -3x+\frac{4}{3}y+1=0 równoległa
jest prosta określona wzorem y=......\cdot x+b.
Podaj brakującą liczbę.
Odpowiedź:
| a= | |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11137 |
Podpunkt 9.1 (1 pkt)
» Liczba a spełnia równanie:
Dane
a=4
Odpowiedzi:
| A. \frac{x-3}{x-3}=\frac{-6x-3}{-6x-3} | B. \frac{x+5}{x+5}=\frac{2x-3}{3x+4} |
| C. \frac{x+1}{x+7}=\frac{9x-5}{4x-5} | D. \frac{x+4}{x-2}=\frac{5x+2}{3x-1} |
| Zadanie 10. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20816 |
Podpunkt 10.1 (1 pkt)
W ciągu arytmetycznym (a_n) dane są sumy:
a_{8}+a_{11}=-26 oraz
a_{2}+a_{13}=30.
Wyznacz różnicę tego ciągu.
Odpowiedź:
r=
(wpisz liczbę całkowitą)
Podpunkt 10.2 (1 pkt)
Oblicz a_1
Odpowiedź:
a_1=
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20186 |
Podpunkt 11.1 (1 pkt)
» Rozwiąż równanie z niewiadomą x:
7-3x^2+6x^3-14x=0
.
Podaj najmniejsze z rozwiązań tego równania.
Odpowiedź:
| x_{min}= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 11.2 (1 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
| x_{max}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20295 |
Podpunkt 12.1 (2 pkt)
» Dana jest funkcja
f(x)=
\begin{cases}
2x+1\text{, dla } x\leqslant 0 \\
x+2\text{, dla } x > 0
\end{cases}
Podaj sumę wszystkich miejsc zerowych tej funkcji.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20924 |
Podpunkt 13.1 (1 pkt)
Wykresem funkcji kwadratowej f(x)=ax^2+bx+c jest parabola o wierzchołku
W=(0,-9), a jednym z miejsc zerowych tej funkcji
jest liczba 3.
Podaj współczynnik a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 13.2 (1 pkt)
Podaj współczynniki b i
c.
Odpowiedzi:
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20257 |
Podpunkt 14.1 (2 pkt)
» Kąt \beta jest ostry. Oblicz
\sin\beta+\cos\beta.
Dane
\tan\beta=\frac{3}{4}=0.75000000000000
Odpowiedź:
| \sin\beta+\cos\beta= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20367 |
Podpunkt 15.1 (2 pkt)
Do wykresu paraboli y=2x^2-3x-1 należy punkt
Q=(2am, y) taki, że różnica
2am-y jest największa z możliwych.
Podaj m.
Dane
a=4
Odpowiedź:
| m= | |
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20721 |
Podpunkt 16.1 (2 pkt)
Punkt O jest środkiem okręgu:
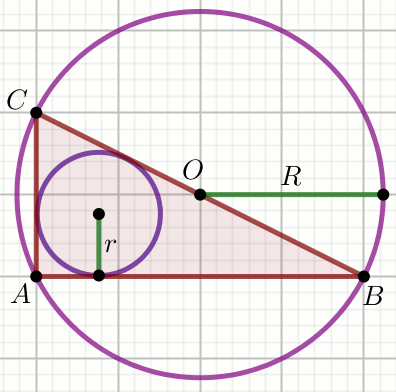

Oblicz r+R.
Dane
|AC|=30
|AB|=16
|AB|=16
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20592 |
Podpunkt 17.1 (1 pkt)
» Punkty A=(3p^2+6p+4, 3-m) oraz
B=(p+2,2m-1) są symetryczne względem osi
Ox.
Podaj m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
Podpunkt 17.2 (1 pkt)
Podaj największe możliwe p.
Odpowiedź:
| p_{max}= | |
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20883 |
Podpunkt 18.1 (1 pkt)
« Kąt ostry DAB równoległoboku
ABCD, w którym |AB|=3 i
|AD|=5, ma miarę 30^{\circ}.
Oblicz długość krótszej przekątnej tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 18.2 (1 pkt)
Oblicz długość dłuższej przekątnej tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20490 |
Podpunkt 19.1 (2 pkt)
Rozwiąż równanie
\frac{ax+b}{cx+d}=\frac{p}{q}
.
Podaj rozwiązanie tego równania.
Dane
a=2
b=-3
c=-2
d=-3
p=-3
q=4
b=-3
c=-2
d=-3
p=-3
q=4
Odpowiedź:
| x= | |
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20815 |
Podpunkt 20.1 (2 pkt)
Ciąg liczbowy (a_n) określony jest wzorem
a_n=n^2+bn+c.
Oblicz sumę wszystkich wyrazów ujemnych tego ciągu.
Dane
b=-\frac{25}{2}=-12.50000000000000
c=\frac{75}{2}=37.50000000000000
c=\frac{75}{2}=37.50000000000000
Odpowiedź:
| s= | |