Podgląd arkusza : lo2@am-3-2022-10-16-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11527 |
Podpunkt 1.1 (1 pkt)
Oblicz wartość wyrażenia w=0,25\cdot 2^{4}\cdot \frac{\sqrt{18}\cdot \sqrt{75}}{\sqrt{6}}.
Odpowiedź:
w=
(wpisz liczbę całkowitą)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10936 |
Podpunkt 2.1 (1 pkt)
« Dana jest funkcja liniowa określona wzorem f(x)=3x-6.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : miejscem zerowym tej funkcji jest liczba 2 | T/N : wykres tej funkcji przecina oś rzędnych w punkcie (0,-6) |
| T/N : funkcja f rośnie w \mathbb{R} |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10479 |
Podpunkt 3.1 (1 pkt)
Na rysunku
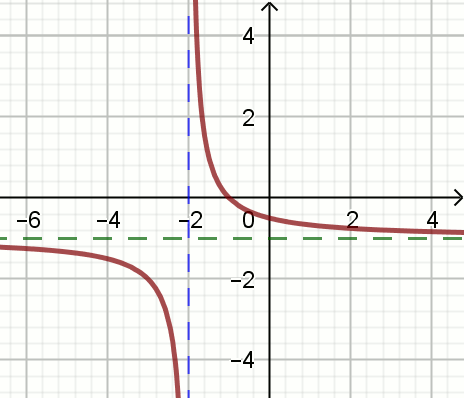

pokazano wykres funkcji symetrycznej względem osi Ox do wykresu funkcji:
Odpowiedzi:
| A. h(x)=-1-\frac{2}{x+2} | B. h(x)=-\frac{1}{x+1}+2 |
| C. h(x)=-\frac{1}{x-2}+1 | D. h(x)=1-\frac{1}{x+2} |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10596 |
Podpunkt 4.1 (1 pkt)
« Odcinki DE i AB
są równoległe, przy czym
|DE|=\frac{1}{6} i
|AB|=\frac{3}{4}:
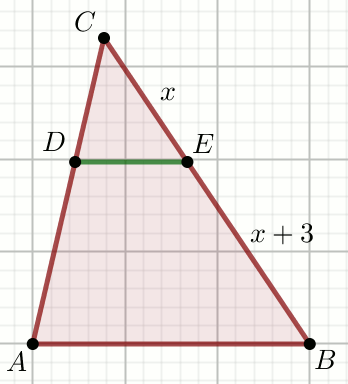

Oblicz x.
Odpowiedź:
| x= | |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10611 |
Podpunkt 5.1 (1 pkt)
Kąt \alpha jest ostry oraz
\tan\alpha=\frac{5}{3}.
Oblicz wartość wyrażenia \frac{2-\cos\alpha}{2+\cos\alpha}.
Odpowiedź:
| \frac{2-\cos\alpha}{2+\cos\alpha}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11021 |
Podpunkt 6.1 (1 pkt)
Wykres funkcji
f(x)=-(x+3)^2-2 pokazany jest na rysunku:
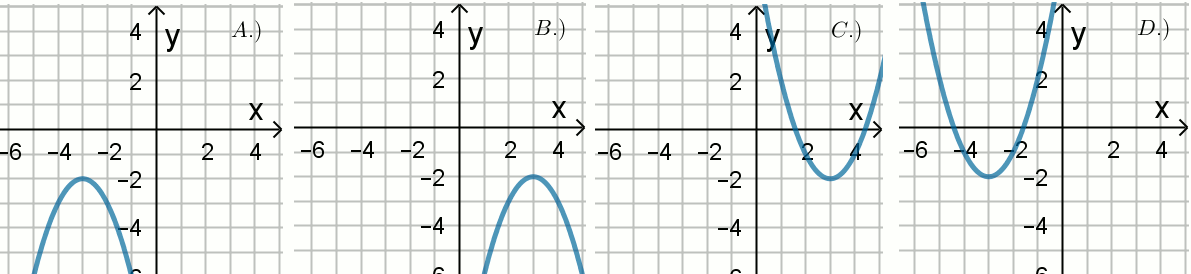

Odpowiedzi:
| A. D | B. A |
| C. C | D. B |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11649 |
Podpunkt 7.1 (1 pkt)
W okręgu o promieniu 58 narysowano cięciwę,
która znajduje się w odległości 42
od środka tego okręgu.
Oblicz długość tej cięciwy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11236 |
Podpunkt 8.1 (1 pkt)
Proste o równaniach x-y+\frac{4}{3}=0 i
-3y+5=0:
Odpowiedzi:
| A. przecinają się pod kątem 30^{\circ} | B. są prostopadłe |
| C. przecinają się pod kątem 60^{\circ} | D. przecinają się pod kątem 45^{\circ} |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-11626 |
Podpunkt 9.1 (1 pkt)
Wielomian 21x^5-22x^4+21x^3-22x^2+21x-22
ma dokładnie jeden pierwiastek wymierny. Jest nim liczba:
Odpowiedzi:
| A. \frac{11}{14} | B. \frac{11}{12} |
| C. \frac{6}{14} | D. \frac{22}{21} |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11385 |
Podpunkt 10.1 (1 pkt)
Dany jest ciąg (a_n) określony wzorem
a_n=\frac{1-4n}{-3n+2}.
Wyraz a_{2k+p} tego ciągu jest równy:
Dane
p=3
Odpowiedzi:
| A. \frac{8k+13}{6k+7} | B. \frac{8k+11}{6k+11} |
| C. \frac{8k+13}{6k+11} | D. \frac{8k+11}{6k+7} |
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20056 |
Podpunkt 11.1 (2 pkt)
» Wyznacz zbiór tych wartości x, które spełniają
nierówność podwójną:
\frac{x-1-2a}{3} \leqslant \frac{2x+1-4a}{2} \lessdot \frac{3x+2-6a}{4}
.
Podaj najmniejszą liczbę spełniającą tę nierówność. Jeśli nierówność jest sprzeczna, wpisz liczbę zero.
Dane
a=-2
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20251 |
Podpunkt 12.1 (2 pkt)
« W trapezie dane są długości podstaw i ramion:
|CD|=\frac{15}{4},
|AB|=6,
|AD|=3 i
|BC|=\frac{9}{4}.
Ramiona trapezu przedłużono
do przecięcia w punkcie O.
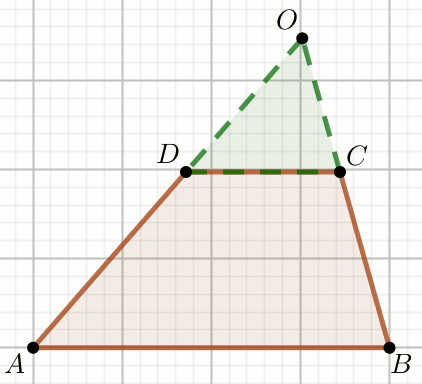
Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.

Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.
Odpowiedź:
| L_{\triangle ABC}= | |
| Zadanie 13. (3 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21016 |
Podpunkt 13.1 (1 pkt)
Promienie okręgów na rysunku są równe: r_1=3m-9 i
r_2=7-m, a odcinek O_1O_2 ma
długośc 8:
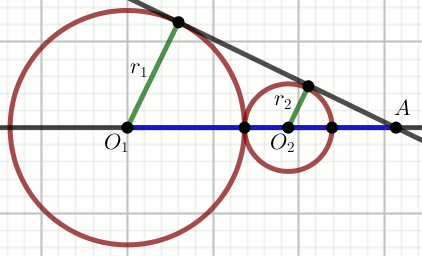

Wyznacz wartość parametru m.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.2 (1 pkt)
Podaj długości tych promieni.
Odpowiedzi:
| r_{min} | = |
(wpisz liczbę zapisaną dziesiętnie) |
| r_{max} | = |
(wpisz liczbę zapisaną dziesiętnie) |
Podpunkt 13.3 (1 pkt)
Oblicz długość odcinka O_1A.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20995 |
Podpunkt 14.1 (1 pkt)
Wielomian W(x)=
-5x^3-\frac{5}{2}x^2+\frac{135}{2}x+90
jest podzielny przez dwumian P(x)=x-4.
Wyznacz pierwiastki tego wielomianu.
Podaj najmniejszy pierwiastek tego wielomianu.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 14.2 (1 pkt)
Podaj pierwiastek niecałkowity tego wielomianu.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20516 |
Podpunkt 15.1 (2 pkt)
« Dany jest ciąg a_n=an^2+bn+c, dla
n\in\mathbb{N_{+}}.
Oblicz ilość wyrazów ujemnych tego ciągu.
Dane
a=2
b=-4
c=-160
b=-4
c=-160
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 16. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30025 |
Podpunkt 16.1 (2 pkt)
« Z punktu A odległego o 96
km od punktu B wyjechał tramwaj. Po godzinie z punktu
B wyjechał inny tramwaj i poruszał się w kierunku
punktu A, po tej samej trasie. Po pewnym
czasie oba tramwaje wyminęły się. Od tego momentu tramwaj jadący z miejscowości
A jechał jeszcze 150 minut
do miejscowości B, a tramwaj drugi jechał jeszcze
przez 210 minut do miasta
A.
Z jaką średnią prędkością poruszał się na trasie tramwaj jadący z miejscowości A?
Odpowiedź:
v_A=
(wpisz liczbę całkowitą)
Podpunkt 16.2 (2 pkt)
Z jaką średnią prędkością poruszał się na trasie tramwaj jadący z miejscowości
B?
Odpowiedź:
v_B=
(wpisz liczbę całkowitą)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20493 |
Podpunkt 17.1 (2 pkt)
«« Jaką miarę łukową ma kąt wypukły utworzony przez wskazówki zegara o godzinie
14:20?
Odpowiedź:
| odp\ [rd]= | |
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20193 |
Podpunkt 18.1 (1 pkt)
Wielomian P(x)=x^5+ax^3+12x^2+bx-24 dzieli
się przez wielomian Q(x)=12+x+x^3.
Wyznacz liczby a i b.
Podaj a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 18.2 (1 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20753 |
Podpunkt 19.1 (2 pkt)
Punkt o współrzędnych A=(x_A,y_A) jest środkiem
symetrii wykresu funkcji homograficznej
f(x)=\frac{ax+b}{x+d}.
Oblicz \frac{a}{d}.
Dane
x_A=3
y_A=-5
y_A=-5
Odpowiedź:
| \frac{a}{d}= | |
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20251 |
Podpunkt 20.1 (1 pkt)
« Prawdziwe jest zdanie:
\forall x\in\mathbb{R}:
\frac{12-2x}{3x+m-15} \lessdot 0 \iff x\in(-\infty,3)\cup (6,+\infty)
.
Podaj m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
Podpunkt 20.2 (1 pkt)
Dla wyznaczonej wartości m rozwiąż nierówność:
\frac{-2x+14}{3x+m-18} \leqslant -4
.
Podaj długość rozwiązania.
Odpowiedź:
| \frac{k}{n}= | |