Podgląd arkusza : lo2@am-3-2022-10-23-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10446 |
Podpunkt 1.1 (1 pkt)
Zapisz wyrażenie
\frac{\sqrt{6}+6}{\sqrt{6}-6}
w najprostszej postaci \frac{m+n\sqrt{k}}{p},
gdzie m,n,k,p\in\mathbb{Z}.
Podaj liczby m, n, k i p.
Odpowiedź:
| \frac{m+n\sqrt{k}}{p}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11406 |
Podpunkt 2.1 (0.5 pkt)
Miejscem zerowym funkcji liniowej
f(x)=3(x+4)-6\sqrt{3} jest liczba
a+b\sqrt{3}.
Podaj a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 2.2 (0.5 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11702 |
Podpunkt 3.1 (0.5 pkt)
Rozwiąż układ równań metodą przeciwnych współczynników:
\begin{cases}
1,2x-\frac{2}{5}y=\frac{176}{5} \\
\frac{2}{3}y+0,2x=\frac{11}{15}
\end{cases}
Podaj x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 3.2 (0.5 pkt)
Podaj y.
Odpowiedź:
y=
(wpisz liczbę całkowitą)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10579 |
Podpunkt 4.1 (1 pkt)
Z prostokąta ABCD o obwodzie
30 wycięto trójkąt równoboczny
AOD o obwodzie 15
(tak jak na rysunku).
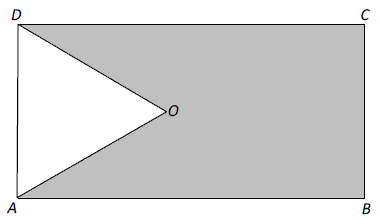

Obwód zacieniowanej figury jest równy:
Odpowiedź:
L=
(wpisz liczbę całkowitą)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10184 |
Podpunkt 5.1 (1 pkt)
Oceń, które z poniższych równości są prawdziwe dla każdej liczby rzeczywistej
x:
Odpowiedzi:
| T/N : \sqrt{(x-2)^2}=x-2 | T/N : |x-3|=|-x-3| |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10983 |
Podpunkt 6.1 (1 pkt)
Wierzchołek paraboli y=x^2+16x leży na prostej
o równaniu:
Odpowiedzi:
| A. y=-16x | B. y=-4x |
| C. y=16x | D. y=-8x |
| E. y=8x | F. y=4x |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10560 |
Podpunkt 7.1 (1 pkt)
« W trójkąt równoramienny ABC o podstawie
AB wpisano okrąg o środku O.
Wiadomo, że |\sphericalangle BOA|=130^{\circ}.
Oblicz miarę stopniową kąta BCA.
Odpowiedź:
|\sphericalangle BCA|=
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10656 |
Podpunkt 8.1 (1 pkt)
« Przekątne równoległoboku mają długość
10 i 12,
a kąt między tymi przekątnymi ma miarę
30^{\circ}.
Oblicz pole powierzchni tego równoległoboku.
Odpowiedź:
| P= | |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11681 |
Podpunkt 9.1 (1 pkt)
« Wielomian określony wzorem W(x)=x^5-3x^4+mx^3+6 przy
dzieleniu przez dwumian x-1 daje resztę
3.
Wyznacz liczbę m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 10. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20827 |
Podpunkt 10.1 (2 pkt)
« Pan Kozłowski złożył do banku kwotę k zł, na procent prosty,
w którym odsetki nie podlegają oprocentowaniu. Po upływie pierwszego i każdego następnego
roku (oprócz końca roku ostatniego) wpłacał kwotę d zł.
Przez cały okres oszczędzania oprocentowanie w banku było stałe i wynosiło
p\% w stosunku rocznym.
Oblicz wartość tej lokaty po n latach (przed opodatkowaniem, po n-tym roku pan Kozłowski nie dopłacił kwoty d zł, tylko wybrał z banku pieniądze na lokacie).
Dane
k=6000
d=1000
p=6.0
n=6
d=1000
p=6.0
n=6
Odpowiedź:
s=
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20954 |
Podpunkt 11.1 (2 pkt)
Autobus pokonał trasę z miasta A do miasta B ze średnią
prędkością 126 km/h, po czym natychmiast zawrócił i pokonał trasę powrotną
ze średnią prędkością 63 km/h.
Jaka była średnia prędkość autobusu na całej trasie?
Odpowiedź:
| v_{sr}= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20775 |
Podpunkt 12.1 (1 pkt)
Dana jest funkcja f(x)=a-|b-x|.
Podaj najmniejsze miejsce zerowe tej funkcji.
Dane
a=\frac{5}{2}=2.50000000000000
b=0=0.00000000000000
b=0=0.00000000000000
Odpowiedź:
| \frac{m}{n}= | |
Podpunkt 12.2 (1 pkt)
Podaj największe miejsce zerowe tej funkcji.
Odpowiedź:
| \frac{m}{n}= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20880 |
Podpunkt 13.1 (2 pkt)
Brygada 24 robotników
wykonuje pewną pracę w czasie 3 godzin i 15 minut. W jakim czasie wykona tę samą pracę brygada liczbąca
40 robotników?
Wynik podaj w minutach.
Odpowiedź:
t[min]=
(wpisz liczbę całkowitą)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20277 |
Podpunkt 14.1 (2 pkt)
» Kąt ostry \alpha spełnia równanie
\sin\alpha+\cos\alpha=\frac{\sqrt{7}}{2}.
Oblicz (\sin\alpha-\cos\alpha)^2
Odpowiedź:
| (\sin\alpha-\cos\alpha)^2= | |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20379 |
Podpunkt 15.1 (1 pkt)
Równanie x^2+(m-2)x+49=0 ma dokładnie jedno
rozwiązanie. Wyznacz m.
Podaj najmniejsze możliwe m.
Odpowiedź:
| m_{min}= | |
Podpunkt 15.2 (1 pkt)
Podaj największe możliwe m.
Odpowiedź:
| m_{max}= | |
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20211 |
Podpunkt 16.1 (1 pkt)
« Na trójkącie ostrokątnym ABC opisano okrąg
o środku w punkcie O. Wiedząc, że
|\measuredangle CBO|=\alpha oraz
|\measuredangle CAO|=\beta oblicz miary
stopniowe kątów trójkąta ABC.
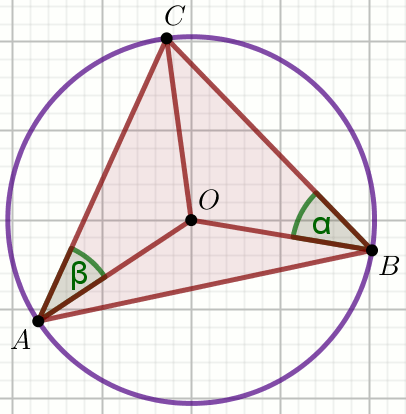

Podaj miarę stopniową najmniejszego z kątów tego trójkąta.
Dane
\alpha=14^{\circ}
\beta=40^{\circ}
\beta=40^{\circ}
Odpowiedź:
\gamma_{min}=
(wpisz liczbę całkowitą)
Podpunkt 16.2 (1 pkt)
Podaj miarę stopniową największego z kątów tego trójkąta.
Odpowiedź:
\gamma_{max}=
(wpisz liczbę całkowitą)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20312 |
Podpunkt 17.1 (2 pkt)
« Dana jest prosta k o równaniu
-x+y-4=0 oraz punkt
P=(5,3). Wyznacz równanie prostej
l równoległej do prostej k
i przechodzącej przez punkt P. Zapisz równanie
prostej l w postaci kierunkowej
y=a_1x+b_1.
Podaj b_1.
Odpowiedź:
| b_1= | |
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20902 |
Podpunkt 18.1 (2 pkt)
« Pole powierzchni trójkąta ABC jest równe 70.
Środkowa CD ma długość 9, a sinus kąta
BDC jest równy \frac{7}{9}.
Oblicz długość boku AB.
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20973 |
Podpunkt 19.1 (2 pkt)
« Oblicz sumę wszystkich pierwiastków wielomianu
P(x)=(18x^3-11x^2-2x)(x^2-15).
Odpowiedź:
| \frac{k}{n}= | |
| Zadanie 20. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11158 |
Podpunkt 20.1 (1 pkt)
« Ciąg liczbowy (a_n) określony jest wzorem
a_n=\frac{an^2+bn+c}{n^2-d}, a liczby
p i q są odpowiednio najmniejszym
i największym numerem wyrazów ciągu, które są równe 0.
Podaj liczby p i q.
Dane
a=2
b=-22
c=48
d=-9
b=-22
c=48
d=-9
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |