Podgląd arkusza : lo2@am-3-2022-11-06-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10397 |
Podpunkt 1.1 (1 pkt)
» Zapisz iloczyn 32^{-3}\cdot \left(\frac{1}{8}\right)^{14}
w postaci a^p, gdzie a,p\in\mathbb{Z}
i a jest liczbą pierwszą.
Podaj liczby a i p.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| p | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10815 |
Podpunkt 2.1 (1 pkt)
Funkcja liniowa f określona jest wzorem
f(x)=mx+n. Funkcja ta spełnia warunek
f(-5)=1, a jej wykres zawiera punkt
(-1,-1).
Wyznacz współczynniki m i n.
Odpowiedzi:
| m | = | (dwie liczby całkowite) | |
| n | = | (dwie liczby całkowite) | |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11622 |
Podpunkt 3.1 (1 pkt)
Do wykresu funkcji kwadratowej należą punkty o współrzędnych
(-1, -2) oraz \left(3,-2\right),
a osią symetrii tego wykresu jest prosta o równaniu x=a.
Wyznacz wartość parametru a.
Odpowiedź:
| \frac{m}{n}= | |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10580 |
Podpunkt 4.1 (1 pkt)
« Oblicz obwód trójkąta równobocznego o polu powierzchni równym 6\sqrt{3}.
Odpowiedź:
m\sqrt{n}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10671 |
Podpunkt 5.1 (1 pkt)
« W trójkącie prostokątnym przyprostokątne mają długość
a i b.
Oblicz cosinus tego kąta ostrego, którego cosinus jest mniejszy.
Dane
a=2\sqrt{5}=4.47213595499958
b=5
b=5
Odpowiedź:
| Wpisz odpowiedź: | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11030 |
Podpunkt 6.1 (1 pkt)
Wskaż funkcję kwadratową, której zbiorem wartości jest przedział
\langle 1,+\infty):
Odpowiedzi:
| A. y=-2(x+3)^2-1 | B. y=-(x+4)^2+1 |
| C. y=(x-2)^2-1 | D. y=(x+3)^2-1 |
| E. y=(x+3)^2+1 | F. y=-(x-1)^2+1 |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10486 |
Podpunkt 7.1 (1 pkt)
Punkt O jest środkiem okręgu na rysunku:
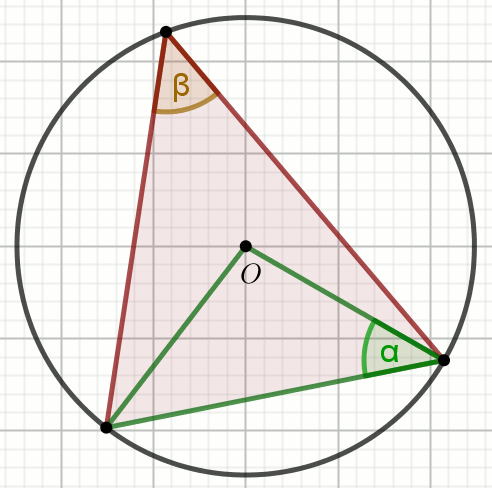
Wiedząc, że \alpha=26^{\circ}, wyznacz miarę stopniową kąta \beta.

Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10904 |
Podpunkt 8.1 (0.5 pkt)
Wykres funkcji liniowej określonej wzorem y=ax+b jest nachylony do osi
Ox pod kątem o mierze 120^{\circ}
i przechodzi przez punkt
\left(\frac{\sqrt{3}}{3},\frac{7}{3}\right).
Wyznacz współczynnik a.
Odpowiedź:
a=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 8.2 (0.5 pkt)
Wyznacz współczynnik b.
Odpowiedź:
| b= | |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11136 |
Podpunkt 9.1 (1 pkt)
» Zbiór A zawiera wspólne rozwiązania równań
\frac{1}{m}x^3=nx i
\frac{1}{a}x^2+bx+c=0.
Podaj liczbę \overline{\overline{A}} (ilość elementów w zbiorze).
Dane
m=8
n=18
a=2
b=-78
c=864
n=18
a=2
b=-78
c=864
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 10. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20506 |
Podpunkt 10.1 (2 pkt)
W ciągu arytmetycznym (a_n) występują kolejne
liczby naturalne dające resztę 2 przy dzieleniu
przez 5.
Wiedząc, że a_{2}=102, oblicz a_{10}.
Odpowiedź:
a_k=
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20157 |
Podpunkt 11.1 (1 pkt)
Rozwiąż równanie z niewiadomą x:
(x-2)(x-4)=-2(x-2)
.
Podaj najmniejsze z rozwiązań tego równania.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 11.2 (1 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20768 |
Podpunkt 12.1 (2 pkt)
Wyznacz dziedzinę funkcji:
f(x)=\frac{\sqrt{x+a}}{x+b}
.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę wszystkich końców liczbowych tych przedziałów.
Dane
a=5
b=3
b=3
Odpowiedź:
suma=
(wpisz liczbę całkowitą)
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20326 |
Podpunkt 13.1 (1 pkt)
» Kinga jest o 8 lat starsza od Kamila.
2 lat temu Kamil był dwa razy młodszy pod Kingi.
Ile lat ma teraz Kamil.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 13.2 (1 pkt)
Ile lat ma teraz Kinga.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20921 |
Podpunkt 14.1 (1 pkt)
Rozwiąż układ równań:
\begin{cases}
\sqrt{3}x+2y=\sqrt{6}\\
\sqrt{2}x-\sqrt{6}y=-3
\end{cases}
.
Podaj x.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.2 (1 pkt)
Podaj y.
Odpowiedź:
| y= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20357 |
Podpunkt 15.1 (1 pkt)
« Dana jest funkcja f(x)=ax^2+bx+c.
Oblicz najmniejszą i największą wartość tej funkcji w przedziale
\langle p,q\rangle.
Podaj wartośc najmniejszą.
Dane
a=-1
b=\frac{1}{2}=0.50000000000000
c=\frac{31}{16}=1.93750000000000
p=-2
q=3
b=\frac{1}{2}=0.50000000000000
c=\frac{31}{16}=1.93750000000000
p=-2
q=3
Odpowiedź:
| min= | |
Podpunkt 15.2 (1 pkt)
Podaj wartośc największą.
Odpowiedź:
| max= | |
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20717 |
Podpunkt 16.1 (2 pkt)
« Długość promienia okręgu opisanego na trójkącie równobocznym jest o
d większa od długości promienia okręgu
wpisanego w ten trójkąt.
Oblicz pole powierzchni tego trójkąta.
Dane
d=3\sqrt{6}=7.34846922834953
Odpowiedź:
P_{\triangle}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20585 |
Podpunkt 17.1 (1 pkt)
» Punkty A=(1,2) i
B=(2,3) należą do prostej
określonej równaniem y=ax+b.
Podaj a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 17.2 (1 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20760 |
Podpunkt 18.1 (2 pkt)
» Trójkąt ABC jest ostrokątny i równoramienny o
podstawie AB:
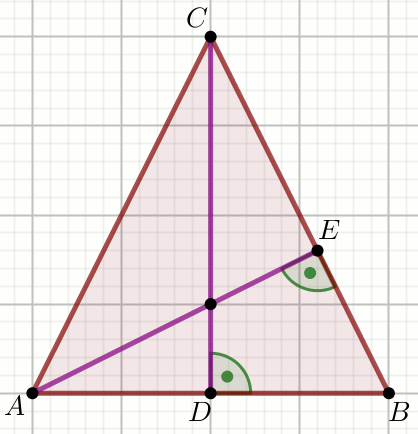

Oblicz P_{ABC}.
Dane
|AB|+|BC|+|AC|=160
\frac{P_{\triangle ABE}}{P_{\triangle ADC}}=\frac{36}{25}=1.44000000000000
\frac{P_{\triangle ABE}}{P_{\triangle ADC}}=\frac{36}{25}=1.44000000000000
Odpowiedź:
P_{\triangle ABC}=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20502 |
Podpunkt 19.1 (2 pkt)
Rowerzysta przejechał drogą leśną s_1 km z prędkością
v, po czym przejechał drogą polną
s_2 kilometrów z prędkością o
20 km/h większą. Oba odcinki drogi pokonał w tym
samym czasie.
Wyznaczv.
Dane
s1=2
s2=8
s2=8
Odpowiedź:
| v= | |
| Zadanie 20. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11387 |
Podpunkt 20.1 (1 pkt)
« Oceń, które z podanych ciągów są malejące?
Odpowiedzi:
| T/N : a_n=1-\frac{4}{n+1} | T/N : a_n=4-\frac{7}{n} |
| T/N : a_n=n^2-n-2 |