Podgląd arkusza : lo2@am-3-2022-11-06-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10433 |
Podpunkt 1.1 (1 pkt)
Zapisz wyrażenie
\frac{4^{9}\cdot 5^{7}}
{20^{7}}
w postaci potęgi p^k o całkowitym wykładniku i podstawie, która
jest liczbą pierwszą.
Podaj podstawę i wykładnik tej potęgi.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| k | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10815 |
Podpunkt 2.1 (1 pkt)
Funkcja liniowa f określona jest wzorem
f(x)=mx+n. Funkcja ta spełnia warunek
f(-4)=6, a jej wykres zawiera punkt
(1,3).
Wyznacz współczynniki m i n.
Odpowiedzi:
| m | = | (dwie liczby całkowite) | |
| n | = | (dwie liczby całkowite) | |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10869 |
Podpunkt 3.1 (1 pkt)
« Dane jest równanie -4x+9y-3=0. Z którym z poniższych
równań tworzy ono układ równań sprzeczny:
Odpowiedzi:
| A. -4x-9y-3=0 | B. -8x-9y-3=0 |
| C. -8x-9y+3=0 | D. -8x+18y+6=0 |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10592 |
Podpunkt 4.1 (1 pkt)
Oblicz długość odcinka x:
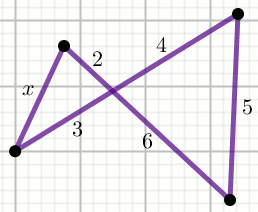

Odpowiedź:
| x= | |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-11599 |
Podpunkt 5.1 (1 pkt)
Wykres funkcji określonej wzorem y=f(x) przecina oś
Oy w punkcie o współrzędnych (0,-11),
a wykres funkcji określonej wzorem y=f\left(|x|\right) przecina oś
Oy w punkcie o współrzędnych (x_0,y_0).
Podaj liczby x_0 i y_0.
Odpowiedzi:
| x_0 | = |
(wpisz liczbę całkowitą) |
| y_0 | = |
(wpisz liczbę całkowitą) |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11054 |
Podpunkt 6.1 (1 pkt)
Pole powierzchni figury ograniczonej parabolą o równaniu y=x^2-9
i osią Ox jest:
Odpowiedzi:
| A. większe od 54 | B. mniejsze od 27 |
| C. równe 27 | D. większe od 27 |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10571 |
Podpunkt 7.1 (1 pkt)
Cięciwa okręgu ma długość 80 cm i jest oddalona od
środka tego okręgu o \frac{39}{2} cm.
Oblicz długość promienia tego okręgu.
Odpowiedź:
| r= | |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10218 |
Podpunkt 8.1 (1 pkt)
Punkt S=(-2,10) jest środkiem okręgu, a do tego okręgu
należy punkt o współrzędnych (-5,6). Okrąg ten opisany jest
równaniem (x-a)^2+(y-b)^2=r^2, gdzie
r > 0.
Podaj liczby a, b i r.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| r | = |
(wpisz liczbę całkowitą) |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-11604 |
Podpunkt 9.1 (1 pkt)
« Wielomian W(x)=ax^3+56x^2+49x ma pierwiastek
dwukrotny.
Wyznacz dodatnią wartość parametru a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11156 |
Podpunkt 10.1 (1 pkt)
« Dany jest ciąg (b_n), w którym
b_n=(n+a)(n+b). Ciąg ten zawiera
k^2 wyrazów ujemnych.
Wyznacz k.
Dane
a=3
b=-257
b=-257
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20085 |
Podpunkt 11.1 (2 pkt)
Rozwiąż równanie z niewiadomą x:
\frac{x^2-3}{10x}=\frac{x^3-1}{10(x^2+3)}
.
Odpowiedź:
| x= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21023 |
Podpunkt 12.1 (1 pkt)
«Wyznacz wartości parametrów a i b,
dla których rozwiązaniem układu równań
\begin{cases}
(a+2b+9)x-(b+1)y=6 \\
5x-(a+b+8)y=2a+14
\end{cases}
jest para liczb (2,2).
Podaj a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 12.2 (1 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20207 |
Podpunkt 13.1 (1 pkt)
« Punkt O jest środkiem okręgu, w którym
AB\parallel CD:
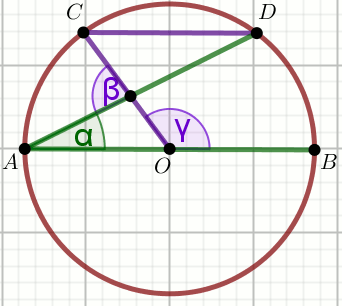

Podaj miarę stopniową kąta \beta.
Dane
\alpha=26^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.2 (1 pkt)
Podaj miarę stopniową kąta \gamma.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30151 |
Podpunkt 14.1 (4 pkt)
« Basen jest napełniany wodą płynącą jednocześnie z kranów
A i B w czasie
t godzin.
Gdyby napełniać basen wodą płynącą tylko z kranu A, to trwałoby to o a godzin krócej niż napełnianie tylko przy użyciu kranu B.
Gdyby napełniać basen wodą płynącą tylko z kranu A, to trwałoby to o a godzin krócej niż napełnianie tylko przy użyciu kranu B.
Ile minut basen jest napełniany wodą płynącą tylko z kranu B?
Dane
a=12
t=8
t=8
Odpowiedź:
t\ [min]=
(wpisz liczbę całkowitą)
| Zadanie 15. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30156 |
Podpunkt 15.1 (2 pkt)
Ciąg arytmetyczny (a_n) określony jest wzorem
a_n=a-bn, dla
n\geqslant 1.
Ile wyrazów dodatnich ma ten ciąg.
Dane
a=2017
b=9
b=9
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 15.2 (2 pkt)
Wyznacz sumę wszystkich wyrazów dodatnich tego ciągu.
Odpowiedź:
s_{> 0}=
(wpisz liczbę całkowitą)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-21082 |
Podpunkt 16.1 (1 pkt)
Rozwiąż równanie
6-|-3-2x|=|-19-6x|
.
Podaj najmniejsze rozwiązanie tego równania.
Odpowiedź:
| x_{min}= | |
Podpunkt 16.2 (1 pkt)
Podaj największe rozwiązanie tego równania.
Odpowiedź:
| x_{max}= | |
| Zadanie 17. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30293 |
Podpunkt 17.1 (2 pkt)
« Rozwiąż układ
\begin{cases}
(x-10)^2+y^2=100 \\
|x|+|y|=20
\end{cases}
.
Ile rozwiązań ma ten układ?
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
Podpunkt 17.2 (1 pkt)
Podaj współrzędne tego z rozwiązań, które ma największą rzędną.
Odpowiedzi:
| x | = |
(wpisz liczbę całkowitą) |
| y | = |
(wpisz liczbę całkowitą) |
Podpunkt 17.3 (1 pkt)
Podaj współrzędne tego z rozwiązań, które ma najmniejszą odciętą.
Odpowiedzi:
| x | = |
(wpisz liczbę całkowitą) |
| y | = |
(wpisz liczbę całkowitą) |
| Zadanie 18. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30152 |
Podpunkt 18.1 (2 pkt)
« Dana jest funkcja
f(x)=|x^3-3\sqrt{5}x^2-x+3\sqrt{5}|, której wykres
przesunięto o wektor
\vec{u}=[-3\sqrt{5}, -\sqrt{5}],
w wyniku czego otrzymano wykres funkcji g. Dla jakich
argumentów funkcja g osiąga wartość najmniejszą i
ile ona jest równa?
Podaj najmniejszą wartość funkcji g.
Odpowiedź:
g_{min}(x)=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 18.2 (1 pkt)
Podaj najmniejszy z argumentów, dla którego funkcja g
przyjmuje wartość najmniejszą.
Odpowiedź:
x_{min}=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
Podpunkt 18.3 (1 pkt)
Podaj największy z argumentów, dla którego funkcja g
przyjmuje wartość najmniejszą.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 19. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30173 |
Podpunkt 19.1 (2 pkt)
» Dane jest równanie o niewiadomej x:
\frac{2m-10}{3-2x-x^2}+\frac{3}{x+3}=\frac{1}{m-1}
.
Wyznacz te wszystkie wartości parametru m, dla
których spełniona jest równość
\frac{1}{x_1}+\frac{1}{x_2}=\frac{5}{m-4},
gdzie x_1 i x_2 są
różnymi pierwiastkami tego równania.
Podaj najmniejsze takie m.
Odpowiedź:
m_{min}=
(wpisz liczbę całkowitą)
Podpunkt 19.2 (2 pkt)
Podaj największe takie m.
Odpowiedź:
m_{max}=
(wpisz liczbę całkowitą)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20809 |
Podpunkt 20.1 (1 pkt)
« Dany jest ciąg (a_n), w którym
S_n=a_1+a_2+a_3+...+a_n, dla każdego
n\in\mathbb{N_{+}}. Ponadto dla każdej liczby
naturalnej dodatniej zachodzi wzór:
S_n=\frac{n+1}{p\cdot(n+1)+q}.
Oblicz a_2.
Dane
p=2
q=-2
q=-2
Odpowiedź:
| a_{2}= | |
Podpunkt 20.2 (1 pkt)
Ogólny wyraz tego ciągu określony jest wzorem
a_n=\frac{-1}{bn^2+cn}.
Podaj c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)