Podgląd arkusza : lo2@am-3-2022-11-27-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10273 |
Podpunkt 1.1 (1 pkt)
Oblicz wartość wyrażenia w=\log_{3}{\frac{1}{27}}-\log_{3}{1}.
Odpowiedź:
w=
(wpisz liczbę całkowitą)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10796 |
Podpunkt 2.1 (1 pkt)
« Liczba -\frac{4}{3} jest miejscem zerowym funkcji określonej wzorem
f(x)=\left(1+\frac{a}{8}\right)x+2.
Wyznacz a.
Odpowiedź:
| a= | |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10950 |
Podpunkt 3.1 (1 pkt)
Sznurek o długości 432 metrów pocięto na trzy części,
których stosunek długości jest równy 5:11:20.
Ile metrów ma najdłuższa z tych części?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10659 |
Podpunkt 4.1 (1 pkt)
W trapezie ABCD boki AD
i CD mają taką samą długość, a kąt
\beta ma miarę 140^{\circ}:
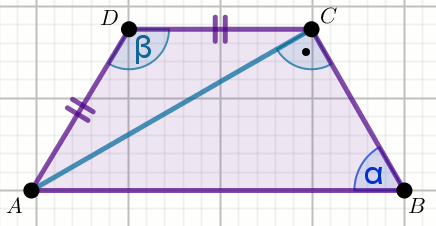

Wyznacz miarę stopniową kąta \alpha.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10777 |
Podpunkt 5.1 (1 pkt)
Na rysunku przedstawiony jest wykres funkcji
y=f(x).
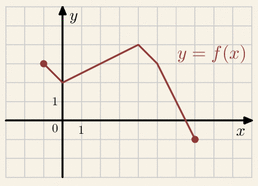
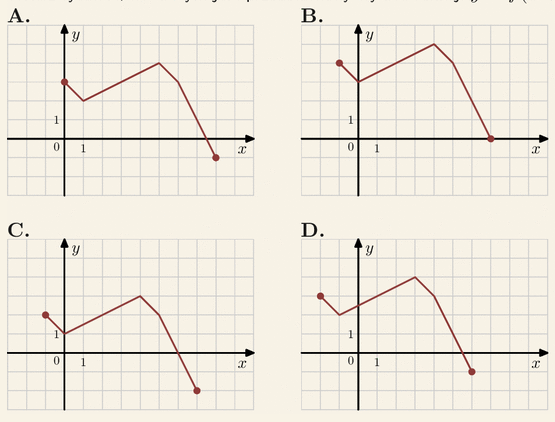

Na którym rysunku przedstawiony jest wykres funkcji y=f(x)+1:

Odpowiedzi:
| A. D | B. A |
| C. C | D. B |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11005 |
Podpunkt 6.1 (0.2 pkt)
« Funkcja y=-(x-2)^2-8 jest rosnąca w pewnym
przedziale liczbowym.
Przedział ten ma postać:
Odpowiedzi:
| A. (p,+\infty) | B. (-\infty,p) |
| C. (-\infty,p\rangle | D. \langle p,q\rangle |
| E. \langle p,+\infty) | F. (p,q) |
Podpunkt 6.2 (0.8 pkt)
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10497 |
Podpunkt 7.1 (1 pkt)
W okręgu poprowadzono cięciwę AB oraz cięciwę
BC (A\neq C). Obie
cięciwy mają długość równą promieniowi okręgu.
Wyznacz miarę stopniową kąta ABC.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11518 |
Podpunkt 8.1 (1 pkt)
(1 pkt)
Do prostej k należą punkty
A=\left(-9,\frac{21}{2}\right) oraz
B=(0,0). Prosta k
nachylona jest do osi Ox pod kątem o mierze
\alpha.
Wynika z tego, że:
Odpowiedzi:
| A. \tan\alpha=-\frac{12}{7} | B. \tan\alpha=-\frac{7}{6} |
| C. \tan\alpha=-\frac{3}{7} | D. \tan\alpha=\frac{7}{6} |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11679 |
Podpunkt 9.1 (1 pkt)
Wyznacz tę wartość parametru m, dla której wielomian
P(x)=6x^3-8x^2-5x+m-1 dzieli się bez reszty przez
dwumian x-1.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11162 |
Podpunkt 10.1 (1 pkt)
« Ogólny wyraz ciągu określony jest wzorem
a_n=7(\sqrt[3]{3})^{n+a}, przy czym
n jest liczbą co najwyżej dwucyfrową.
Wyznacz ilość wyrazów wymiernych tego ciągu.
Dane
a=5
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20092 |
Podpunkt 11.1 (2 pkt)
Rozwiąż równanie (x-2)(2x+1)-(2x-6)(x+2)=3+x
o niewiadomej x.
Odpowiedź:
| x= | |
| Zadanie 12. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30053 |
Podpunkt 12.1 (1 pkt)
« Funkcja f określona jest wzorem
f(x)=-\sqrt{3}x+am+b.
Wyznacz te wartości m, dla których miejscem zerowym funkcji jest liczba \sqrt{3}.
Dane
a=2
b=-8
b=-8
Odpowiedź:
| m= | |
Podpunkt 12.2 (1 pkt)
Dla jakich wartosci m wykres przecina oś
Oy w punkcie o rzędnej 2?
Odpowiedź:
| m= | |
Podpunkt 12.3 (2 pkt)
Dla m=-2 wyznacz współrzędne punktów przecięcia
wykresu z osiami układu.
Ile wynosi suma czterech otrzymanych współrzędnych?
Odpowiedź:
| Wpisz odpowiedź: |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20838 |
Podpunkt 13.1 (1 pkt)
Jeśli do liczby 34 dopiszemy cyfrę z przodu, to otrzymamy
liczbę x. Jeśli do liczby 34
dopiszemy cyfrę z tyłu, to otrzymamy liczbę y. Różnica
x-y jest równa 86, zaś suma
cyfr dopisanych z przodu i z tyłu jesty równa 12.
Podaj x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 13.2 (1 pkt)
Podaj liczbę y.
Odpowiedź:
y=
(wpisz liczbę całkowitą)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20737 |
Podpunkt 14.1 (1 pkt)
Kąt \alpha jest ostry. Oblicz \sin\alpha.
Dane
\tan\alpha=\frac{35}{12}=2.91666666666667
Odpowiedź:
| \sin\alpha= | |
Podpunkt 14.2 (1 pkt)
Oblicz \cos\alpha.
Odpowiedź:
| \cos\alpha= | |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20370 |
Podpunkt 15.1 (1 pkt)
» Funkcja kwadratowa f(x)=32x^2+bx+\frac{1}{2} ma tylko
jedno miejsce zerowe. Oblicz b.
Podaj najmniejszą możliwą wartość b.
Odpowiedź:
| b_{min}= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 15.2 (1 pkt)
Odpowiedź:
| b_{max}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20222 |
Podpunkt 16.1 (2 pkt)
Okręgi są styczne do siebie i boków kwadratu. Stosunek ich promieni wynosi
k:1, a przekątna kwadratu ma długość
d.
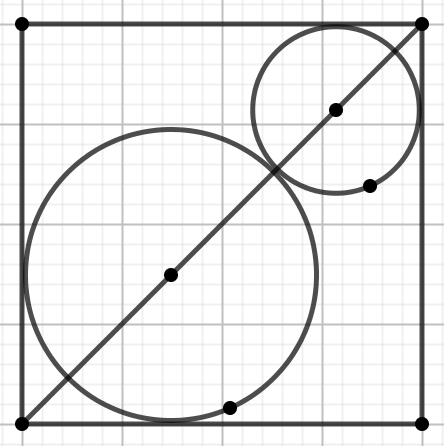

Oblicz promień mniejszego z okręgów.
Dane
k=5
d=8
d=8
Odpowiedź:
| r= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20312 |
Podpunkt 17.1 (2 pkt)
« Dana jest prosta k o równaniu
10x-4y-2=0 oraz punkt
P=(-1,1). Wyznacz równanie prostej
l równoległej do prostej k
i przechodzącej przez punkt P. Zapisz równanie
prostej l w postaci kierunkowej
y=a_1x+b_1.
Podaj b_1.
Odpowiedź:
| b_1= | |
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20887 |
Podpunkt 18.1 (2 pkt)
» Oblicz długość promienia okręgu na rysunku wiedząc, że
|AC|-|AB|=12\sqrt{2} oraz
|BC|=20:
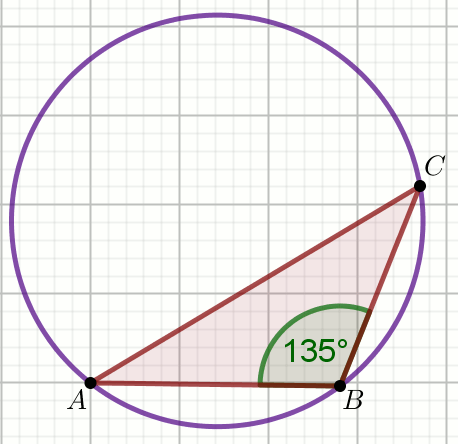

Odpowiedź:
R=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20989 |
Podpunkt 19.1 (2 pkt)
Wielomian W(x)=(8x^3-27)(6x-8) jest podzielny przez
wielomian P(x)=4x^2+6x+9, a wynikiem tego dzielenia jest wielomian
Q(x)=ax^2+bx+c.
Wyznacz liczby a, b i c.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20818 |
Podpunkt 20.1 (1 pkt)
Dany jest ciąg arytmetyczny (a_n).
Wyznacz a_1.
Dane
a_{2}=-18
a_{6}=-6
a_{k}=132
a_{6}=-6
a_{k}=132
Odpowiedź:
a_1=
(wpisz liczbę całkowitą)
Podpunkt 20.2 (1 pkt)
Oblicz k.
Odpowiedź:
k=
(wpisz liczbę całkowitą)