Podgląd arkusza : lo2@am-3-2022-12-11-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10341 |
Podpunkt 1.1 (1 pkt)
Niech k=2-2\sqrt{2}, zaś
m=2-2\sqrt{2}.
Zapisz wartość wyrażenia k^2-6m w najprostszej postaci
a+b\sqrt{c}, gdzie a,b,c\in\mathbb{Z}.
Podaj liczby a i b.
Odpowiedź:
Wpisz odpowiedź:
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10938 |
Podpunkt 2.1 (1 pkt)
Punkt A=(m^2+1,-3) należy do wykresu funkcji liniowej
określonej wzorem g(x)=49-2x:
Odpowiedzi:
| A. dla m\in\{-5,5\} | B. tylko dla m=5 |
| C. tylko dla m=-5 | D. dla m\in\mathbb{R} |
| E. tylko dla m=-10 | F. dla m\in\emptyset |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11627 |
Podpunkt 3.1 (1 pkt)
Wyznacz miejsca zerowe funkcji określonej wzorem
f(x)=-x^2-4x-4.
Odpowiedzi:
| x_{min} | = |
(wpisz liczbę całkowitą) |
| x_{max} | = |
(wpisz liczbę całkowitą) |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10664 |
Podpunkt 4.1 (1 pkt)
Kąt trójkąta prostokątnego ma miarę 56^{\circ}.
Z wierzchołka kąta prostego poprowadzono środkową i wysokość tego trójkąta.
Oblicz miarę stopniową kąta między nimi.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11619 |
Podpunkt 5.1 (1 pkt)
« Wyznacz najmniejsze rozwiązanie równania
\frac{|x-6\sqrt{3}|-1}{3}=2-\sqrt{3}
i zapisz wynik w najprostszej postaci a+b\sqrt{c}.
Odpowiedź:
x_{min}=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10988 |
Podpunkt 6.1 (1 pkt)
» Wyznacz najmniejszą wartość funkcji kwadratowej określonej wzorem
f(x)=x^2+12x.
Odpowiedź:
f_{min}(x)=
(wpisz liczbę całkowitą)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10513 |
Podpunkt 7.1 (1 pkt)
Punkt O jest środkiem okręgu na rysunku, a kąt:
\alpha ma miarę 194^{\circ}:
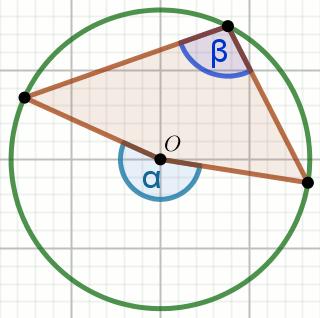

Wyznacz miarę stopniową kąta \beta zaznaczonego na rysunku.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10515 |
Podpunkt 8.1 (1 pkt)
« Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku
9:25, mogą być równe:
Odpowiedzi:
| A. 5:\frac{9}{5} | B. 6:\frac{27}{5} |
| C. 3:\frac{9}{5} | D. 15:6 |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11139 |
Podpunkt 9.1 (1 pkt)
Boki prostokąta mają długości a i
5a. Gdyby każdy z boków wydłużyć o
k, to ich stosunek byłby równy
2.
Wyznacz pole powierzchni tego prostokąta.
Dane
k=12
Odpowiedź:
P_{\square}=
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11508 |
Podpunkt 10.1 (1 pkt)
(1 pkt)
W ciągu geometrycznym \left(a_n\right), określonym
dla każdego n\in\mathbb{N_+}, wyrazy drugi i szósty
są równe odpowiednio a_2=4 i
a_6=16.
Kwadrat wyrazu czwartego tego ciągu jest równy:
Odpowiedź:
a_4^2=
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20169 |
Podpunkt 11.1 (1 pkt)
Rozwiąż równanie z niewiadomą x:
3(x-4)-(-5+x)(x-4)=0
.
Podaj najmniejsze z rozwiązań tego równania.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 11.2 (1 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20840 |
Podpunkt 12.1 (1 pkt)
« Funkcja liniowa f określona wzorem
f(x)=mx+n wartości nieujemne przyjmuje tylko
w przedziale (-\infty, 2\rangle oraz zachodzi
warunek f(-1)=15. Wyznacz wartości współczynników
m i n.
Podaj m.
Odpowiedź:
| m= | |
Podpunkt 12.2 (1 pkt)
Podaj n.
Odpowiedź:
| n= | |
| Zadanie 13. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30396 |
Podpunkt 13.1 (4 pkt)
« Odległość między dwoma miastami
Odległość między dwoma miastami
wynosi 56 km. Pociąg pokonuję tę trasę w określonym
czasie t. Gdyby pociąg jechał o
28 km/h wolniej, to do miasta docelowego
przyjechałby o 160 minut później. Gdyby zaś pociąg jechał
o 14 km/h szybiej, to pokonywałby tę trasę w czasie o
20 minut krótszym.
Ile minut potrzebuje pociąg na pokonanie tej trasy?
Odpowiedź:
t[min]=
(wpisz liczbę całkowitą)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20779 |
Podpunkt 14.1 (1 pkt)
« W trójkącie ABC dane są:
A=(1,-1), B=(-8,-2)
i C=(-4,-6). Oblicz długości boków tego trójkąta.
Podaj długość boku najkrótszego.
Odpowiedź:
min=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 14.2 (1 pkt)
Podaj długość boku najdłuższego.
Odpowiedź:
max=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20397 |
Podpunkt 15.1 (2 pkt)
« Rozwiąż nierówność -x^2+bx+c \lessdot 0.
Ile liczb całkowitych z przedziału \langle -20,20\rangle nie spełnia tej nierówności?
Dane
b=-2
c=-3
c=-3
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20721 |
Podpunkt 16.1 (2 pkt)
Punkt O jest środkiem okręgu:
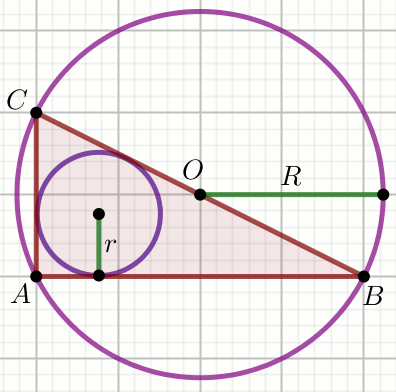

Oblicz r+R.
Dane
|AC|=12
|AB|=5
|AB|=5
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20313 |
Podpunkt 17.1 (2 pkt)
« Dane są punkty o współrzędnych A=(6,7),
B=(3,-3) i C=(7,10).
Prosta k:y=mx+n przechodzi przez punkt
C i jest prostopadła do odcinka
AB. Wyznacz równanie prostej
k.
Podaj m+n.
Odpowiedź:
| m+n= | |
| Zadanie 18. (3 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20911 |
Podpunkt 18.1 (1 pkt)
Dwa boki trójkąta ostrokątnego mają długość 10 i 11, a jego
pole powierzchni jest równe \frac{55}{3}.
Oblicz sinus kąta zawartego między tymi bokami.
Odpowiedź:
| \sin\alpha= | |
Podpunkt 18.2 (1 pkt)
Oblicz długość trzeciego boku tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 18.3 (1 pkt)
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20987 |
Podpunkt 19.1 (2 pkt)
Wielomian W(x)=-10x^3-9x^2-22x-8 jest podzielny przez
wielomian P(x)=ax+b, a wynikiem tego dzielenia jest wielomian
Q(x)=2x^2+x+4.
Wyznacz liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20820 |
Podpunkt 20.1 (1 pkt)
Ile liczb niepodzielnych przez 3 zawiera przedział liczbowy
\left\langle p,q\right)?
Dane
p=220
q=410
q=410
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 20.2 (1 pkt)
Ile jest równa suma tych liczb?
Odpowiedź:
s=
(wpisz liczbę całkowitą)