Podgląd arkusza : lo2@am-3-2022-12-11-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10445 |
Podpunkt 1.1 (1 pkt)
Zapisz wyrażenie
\left(6-\sqrt{2}\right)^2-4\left(3-\sqrt{2}\right)
w najprostszej postaci m+n\sqrt{k}, gdzie
m,n,k\in\mathbb{Z}.
Odpowiedź:
m+n\sqrt{k}=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10753 |
Podpunkt 2.1 (1 pkt)
Wartością funkcji dla argumentu naturalnego n jest
ostatnia cyfra kwadratu liczby n zwiększona o
2. Wynika stąd, że zbiór wartości funkcji zawiera
liczbę:
Odpowiedzi:
| A. 5 | B. 4 |
| C. 7 | D. 9 |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11698 |
Podpunkt 3.1 (1 pkt)
Do wykresu funkcji wykładniczej określonej wzorem
f(x)=a^x,
należy punkt o współrzędnych
\left(-1,5\right).
Wyznacz liczbę a.
Odpowiedź:
| a= | |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11464 |
Podpunkt 4.1 (1 pkt)
Trójkąt ABC ma obwód o długości
55. Punkty A_1,
B_1 i C_1 są środkami
boków trójkąta ABC.
Trójkąt PQR, podobny do trójkąta A_1B_1C_1 w skali \frac{3}{2}.
Trójkąt PQR, podobny do trójkąta A_1B_1C_1 w skali \frac{3}{2}.
Oblicz długość obwodu trójkąta PQR.
Odpowiedź:
| L_{\triangle PQR}= | |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10670 |
Podpunkt 5.1 (1 pkt)
« Trapez na rysunku jest prostokątny:
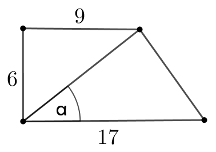

Miara kąta \alpha spełnia warunek:
Odpowiedzi:
| A. 30^{\circ} \lessdot \alpha < 35^{\circ} | B. \alpha=30^{\circ} |
| C. \alpha=45^{\circ} | D. 50^{\circ} \lessdot \alpha < 60^{\circ} |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11080 |
Podpunkt 6.1 (1 pkt)
« Suma dwóch liczb jest równa 24\sqrt{2}, a ich
iloczyn ma największą możliwą wartość.
Oblicz mniejszą z tych liczb.
Odpowiedź:
min=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10476 |
Podpunkt 7.1 (1 pkt)
« Dane są okręgi, w których |O_1A|=35,
|O_2B|=21 i
|O_1O_2|=112:
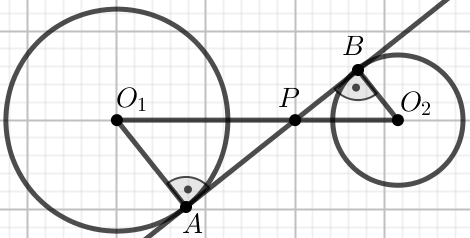

Oblicz długość odcinka O_1P.
Odpowiedź:
|O_1P|=
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10679 |
Podpunkt 8.1 (1 pkt)
Pole powierzchni rombu o obwodzie długości 64 jest równe
64. Kąt ostry tego rombu ma miarę
\alpha.
Wówczas:
Odpowiedzi:
| A. 14^{\circ} \lessdot \alpha \lessdot 15^{\circ} | B. 60^{\circ} \lessdot \alpha \lessdot 61^{\circ} |
| C. 75^{\circ} \lessdot \alpha \lessdot 76^{\circ} | D. 29^{\circ} \lessdot \alpha \lessdot 30^{\circ} |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11556 |
Podpunkt 9.1 (1 pkt)
Suma wielomianów W(x)=-2x^3+5x^2-3 oraz
P(x)=2x^3+12x wynosi:
Odpowiedzi:
| A. 4x^3+12x^2-3 | B. 5x^2+12x-3 |
| C. 4x^3+5x^2+12x-3 | D. 4x^6+5x^2+12x-3 |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11179 |
Podpunkt 10.1 (1 pkt)
W ciągu geometrycznym (a_n), który zawiera dziewięć
wyrazów, wszystkie wyrazy są dodatnie i znane są dwa wyrazy
a_1 i a_9.
Oblicz a_5.
Dane
a_1=8
a_9=18
a_9=18
Odpowiedź:
a_5=
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20849 |
Podpunkt 11.1 (1 pkt)
Ułamek nieskracalny \frac{m}{n} jest równy
liczbie 0,(69).
Podaj m.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (1 pkt)
Podaj n.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20325 |
Podpunkt 12.1 (2 pkt)
» Rozwiąż układ równań
\begin{cases}
3x+2y=3 \\
y+2=\frac{3(1-x)+4}{2}
\end{cases}
.
Punkt A=(4, m) należy do rozwiązania. Podaj m.
Odpowiedź:
| \frac{p}{q}= | |
| Zadanie 13. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30065 |
Podpunkt 13.1 (2 pkt)
» Punkt O=(0,0) należy do wykresu funkcji
kwadratowej y=g(x). Funkcja
h(x)=g(x+1) przyjmuje wartość największą równą
m dla x=n.
Wyznacz wzory obu funkcji w postaci ogólnej.
Podaj sumę współczynników funkcji g.
Dane
m=6
n=5
n=5
Odpowiedź:
| \frac{a}{b}= | |
Podpunkt 13.2 (2 pkt)
Podaj sumę współczynników h.
Odpowiedź:
| \frac{a}{b}= | |
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21001 |
Podpunkt 14.1 (2 pkt)
Iloczyn kwadratu liczby a i kwadratu liczby większej od
a o 3, jest równy
324.
Podaj najmniejszą i największą możliwą wartość liczby a.
Odpowiedzi:
| a_{min} | = |
(wpisz liczbę całkowitą) |
| a_{max} | = |
(wpisz liczbę całkowitą) |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20821 |
Podpunkt 15.1 (1 pkt)
« Suma stu kolejnych liczb naturalnych, które przy dzieleniu przez
10 dają resztę 7
jest równa 52200.
Podaj najmniejszą z tych liczb.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 15.2 (1 pkt)
Podaj największą z tych liczb.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20095 |
Podpunkt 16.1 (1 pkt)
Wyznacz wartości parametru m, dla których dziedziną
funkcji f(x)=\sqrt{(m+3)x^2+x(m+3)+1} jest
zbiór \mathbb{R}.
Podaj najmniejsze takie m.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 16.2 (1 pkt)
Podaj największe takie m.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30197 |
Podpunkt 17.1 (2 pkt)
» Wyznacz te wartości parametru m, dla których
równanie
4\sin^2 2x\cdot \cos^2 2x+\frac{m+9}{2m-2}=4
nie jest sprzeczne.
Podaj najmniejsze możliwe m spełniające warunki zadania.
Odpowiedź:
| m_{min}= | |
Podpunkt 17.2 (2 pkt)
Podaj największe możliwe m spełniające warunki
zadania.
Odpowiedź:
m_{max}=
(wpisz liczbę całkowitą)
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-21009 |
Podpunkt 18.1 (2 pkt)
Wyznacz wszystkie pierwiastki wielomianu W(x)=
6x^3+4x^2+52x-18.
Podaj najmniejszy i największy pierwiastek tego wielomianu.
Odpowiedzi:
| x_{min} | = | (dwie liczby całkowite) | |
| x_{max} | = | (dwie liczby całkowite) | |
| Zadanie 19. (3 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20825 |
Podpunkt 19.1 (1 pkt)
Dana jest funkcja, która nie przyjmuje wartości -2:
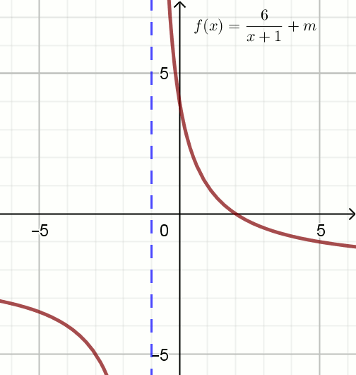

Wyznacz m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
Podpunkt 19.2 (1 pkt)
Wyznacz miejsce zerowe tej funkcji.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 19.3 (1 pkt)
Oblicz f(k\sqrt{2}-1). Wynik zapisz w postaci
a+b\sqrt{2}, gdzie
a,b\in\mathbb{W}.
Podaj a+b.
Dane
k=12
Odpowiedź:
| a+b= | |
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20480 |
Podpunkt 20.1 (2 pkt)
« Oblicz granicę
\lim_{n\to+\infty}
\left(\frac{14n^3+6n+5}{6n^3+1}-\frac{15n^2+2n+1}{5n^2-4}\right)
.
Odpowiedź:
| g= | |