Podgląd arkusza : lo2@am-3-2023-01-08-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10063 |
Podpunkt 1.1 (1 pkt)
» Dla każdego x\in\mathbb{R}-\{-3,-5,4\}
wyrażenie \frac{6}{(x+5)(x+3)}-\frac{4}{(x-4)(x+5)^2}
po sprowadzeniu do wspólnego mianownika ma postać:
Odpowiedzi:
| A. \frac{6(x-4)-4}{(x+3)(x-4)(x+5)^2} | B. \frac{6-4}{(x+3)(x-4)(x+5)^2} |
| C. \frac{6-4(x+3)}{(x+3)(x-4)(x+5)^2} | D. \frac{6(x-4)(x+5)-4(x+3)}{(x+3)(x-4)(x+5)^2} |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10901 |
Podpunkt 2.1 (1 pkt)
Proporcjonalnością prostą jest zależność opisana wzorem:
Odpowiedzi:
| A. y=\frac{169}{x} | B. y=26x^2 |
| C. y=\frac{13}{\sqrt{13}x} | D. y=\frac{\sqrt{13}x}{13} |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10874 |
Podpunkt 3.1 (1 pkt)
Rozwiązaniem układu równań
\begin{cases}
x+4y=\frac{9}{2} \\
8x-8y=-4
\end{cases}
jest para liczb:
Odpowiedzi:
| A. x=-\frac{1}{2}\wedge y=\frac{3}{2} | B. x=\frac{1}{2}\wedge y=1 |
| C. x=\frac{3}{2}\wedge y=1 | D. x=\frac{1}{2}\wedge y=2 |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11568 |
Podpunkt 4.1 (0.5 pkt)
W trapezie podstawy mają długość 9 i
35, a wysokość ma długość 12.
Wyznacz odległości punktu przecięcia się przekątynych tego trapezu od jego podstaw.
Podaj krótszą z tych odległości.
Odpowiedź:
| min= | |
Podpunkt 4.2 (0.5 pkt)
Podaj dłuższą z tych odległości.
Odpowiedź:
| max= | |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10495 |
Podpunkt 5.1 (1 pkt)
Rozwiązaniem nierówności |x-a| \geqslant b jest zbiór
(-\infty, -9\rangle\cup\langle-1,+\infty).
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11427 |
Podpunkt 6.1 (1 pkt)
Funkcja kwadratowa jest określona wzorem
f(x)=-(2x+2)(x+3). Liczby
x_1 i x_2 są różnymi
miejscami zerowymi funkcji f spełniającymi warunek
x_1+x_2=..........
Podaj brakującą liczbę.
Odpowiedzi:
| A. x_1+x_2=8 | B. x_1+x_2=-4 |
| C. x_1+x_2=4 | D. x_1+x_2=-8 |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11677 |
Podpunkt 7.1 (1 pkt)
Zapisz wyrażenie
(9x-5)^2x+(5-9x)x^2-(9x-5) w postaci iloczynu
dwóch wyrażeń w postaci (a_1x^2+b_1x+c_1)(ax+d_1).
Podaj sumę a_1+b_1+c_1.
Odpowiedź:
a_1+b_1+c_1=
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11171 |
Podpunkt 8.1 (1 pkt)
W monotonicznym ciągu geometrycznym a_1=4, a
a_3=81.
Oblicz iloraz tego ciągu.
Odpowiedź:
| q= | |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11272 |
Podpunkt 9.1 (1 pkt)
« Liczba dwucyfrowa jest większa od 41 i składa
się z różnych cyfr.
Ile jest takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10235 |
Podpunkt 10.1 (1 pkt)
« W liczbie 547598 przestawiono cyfry w taki sposób,
że pierwsza i ostatni cyfra tej liczby były równe 5.
Ile takich liczb można otrzymać:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20057 |
Podpunkt 11.1 (2 pkt)
» Wyznacz zbiór tych wartości x, które spełniają
obie nierówności:
\frac{x}{5a}-\frac{x}{4a}+0,1\leqslant 0 \quad\wedge\quad
\frac{x-3a}{4a}\leqslant \frac{x-2a}{3a}
.
Podaj najmniejszą liczbę spełniającą obie nierówności.
Dane
a=4
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20289 |
Podpunkt 12.1 (2 pkt)
« Przyprostokątne trójkąta mają długości 7 i
10, a jeden z kątów ostrych tego trójkąta ma miarę
\beta.
Oblicz \sin\beta\cdot \cos\beta.
Odpowiedź:
| \sin\beta\cdot\cos\beta= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20766 |
Podpunkt 13.1 (2 pkt)
W wycinek kołowy o kącie środkowym \alpha
wpisano okrąg o polu powierzchni P:
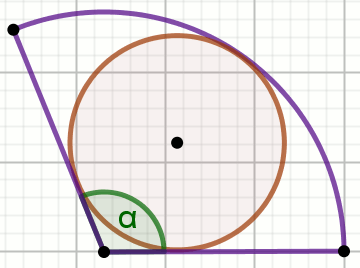

Oblicz pole powierzchni tego wycinka.
Dane
\alpha=120^{\circ}
P=49\pi=153.93804002589987
P=49\pi=153.93804002589987
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20983 |
Podpunkt 14.1 (2 pkt)
Wielomian W(x)\cdot P(x)-H(x), gdzie
W(x)=-3x+5,
P(x)=x^2+ax+b,
H(x)=-3x^3-x^2-5x+25,
jest wielomianem zerowym.
Wyznacz liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 15. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30246 |
Podpunkt 15.1 (2 pkt)
« W rozwinięciu dziesiętnym liczby naturalnej 4
cyfrowej co najmniej jedna cyfra jest parzysta.
Ile jest takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 15.2 (2 pkt)
Podaj ilość takich liczb, że co najmniej jedna cyfra jest nieparzysta.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20040 |
Podpunkt 16.1 (1 pkt)
Rozwiąż nierówność
\left|
\left|
\left|x+2\right|-1
\right|-1
\right|\leqslant 1.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców tych przedziałów, który jest liczbą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 16.2 (1 pkt)
Podaj największy z końców tych przedziałów, który jest liczbą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30289 |
Podpunkt 17.1 (2 pkt)
«« Prosta y=x+2 przecina parabolę
y=-x^2-2x+2 w dwóch punktach
A i B należących do
okręgu o o promieniu długości
\sqrt{5}.
Podaj najmniejszą możliwą odległość środka okręgu o od początku układu współrzędnych.
Odpowiedź:
d_{min}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 17.2 (2 pkt)
Podaj największą możliwą odległość środka okręgu o
od początku układu współrzędnych.
Odpowiedź:
d_{max}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 18. (3 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20825 |
Podpunkt 18.1 (1 pkt)
Dana jest funkcja, która nie przyjmuje wartości -2:
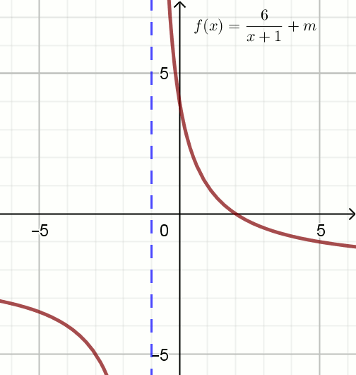

Wyznacz m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
Podpunkt 18.2 (1 pkt)
Wyznacz miejsce zerowe tej funkcji.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 18.3 (1 pkt)
Oblicz f(k\sqrt{2}-1). Wynik zapisz w postaci
a+b\sqrt{2}, gdzie
a,b\in\mathbb{W}.
Podaj a+b.
Dane
k=11
Odpowiedź:
| a+b= | |
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20427 |
Podpunkt 19.1 (2 pkt)
« W liczbie naturalnej k=5 cyfrowej, cyfra
dziesiątek jest o 5 mniejsza od cyfry jedności.
Ile jest takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20513 |
Podpunkt 20.1 (2 pkt)
» Rozwiąż równanie
\frac{1}{6}\cdot \binom{n+10}{n+5}=\binom{n+8}{n+4}
w liczbach naturalnych.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)