Podgląd arkusza : lo2@am-3-2023-01-15-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10306 |
Podpunkt 1.1 (1 pkt)
« Liczba
\frac{\log_{6}{864}+\log_{6}{4}}
{\log_{6}{144}-\log_{6}{4}}
jest równa:
Odpowiedzi:
| A. \frac{2+\log_{6}{16}}{4} | B. \frac{3+\log_{6}{4}}{2} |
| C. \frac{1+\log_{6}{4}}{2} | D. \frac{3+\log_{6}{16}}{2} |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10873 |
Podpunkt 2.1 (1 pkt)
Dany jest układ równań:
\begin{cases}
4y-8x=-8 \\
-5x-y=-19
\end{cases}
.
Określ znaki liczb pary (x,y) spełniającej
ten układ równań:
Odpowiedzi:
| A. x \lessdot 0 \wedge y \lessdot 0 | B. x \lessdot 0 \wedge y > 0 |
| C. x > 0 \wedge y > 0 | D. x > 0 \wedge y \lessdot 0 |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11583 |
Podpunkt 3.1 (1 pkt)
«« Punkty E i F dzielą
przyprostokątne trójkąta ABC w stosunku:
|CE|:|CA|=|BF|:|BA|=\frac{1}{5}, przy czym:
P_{\triangle MCE}=3 i
P_{\triangle NFB}=1:
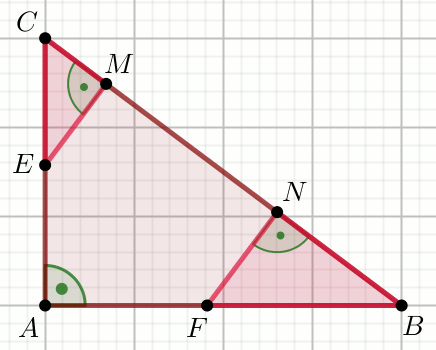

Oblicz pole powierzchni trójkąta ABC.
Odpowiedź:
P_{\triangle ABC}=
(wpisz liczbę całkowitą)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11467 |
Podpunkt 4.1 (0.2 pkt)
Zbiorem wartości funkcji y=-(x-7)(x+7)
określonej dla x\in(3,6\rangle jest pewien przedział liczbowy.
Przedział ten ma postać:
Odpowiedzi:
| A. (p,q) | B. (p,+\infty) |
| C. \langle p,q) | D. (-\infty,p\rangle |
| E. \langle p,q\rangle | F. (p,q\rangle |
Podpunkt 4.2 (0.8 pkt)
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10529 |
Podpunkt 5.1 (1 pkt)
Punkt O jest środkiem okręgu oraz
\alpha=39^{\circ} i
\beta=26^{\circ}:
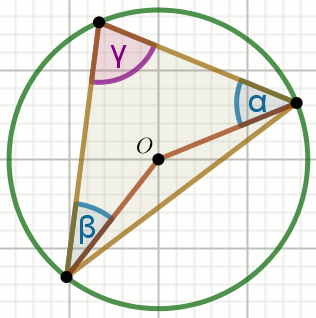

Wyznacz miarę stopniopwą kąta \gamma.
Odpowiedź:
\gamma=
(wpisz liczbę całkowitą)
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11228 |
Podpunkt 6.1 (1 pkt)
« Obwód L rombu o sąsiednich wierzchołkach
A=(3,3) i B=(-9,5)
spełnia nierówność m\leqslant L\lessdot m+1, gdzie
m\in\mathbb{Z}.
Wyznacz liczbę m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11472 |
Podpunkt 7.1 (1 pkt)
Wielomian P(x)=q+4+2x+px^2-2x^4 spełnia
warunki
\begin{cases}
P(-1)+P(1)=0 \\
P(-\sqrt{2})=-P(\sqrt{2})
\end{cases}
.
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11155 |
Podpunkt 8.1 (1 pkt)
» Ile wyrazów ciągu a_n=n^2-a jest mniejszych
od b?
Dane
a=256
b=900
b=900
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11290 |
Podpunkt 9.1 (1 pkt)
« Liczba naturalna dwucyfrowa dzieli się przez jakąkolwiek liczbę ze zbioru
\{8,9\}.
Ile jest takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11259 |
Podpunkt 10.1 (1 pkt)
Przy sklepie, po dwóch stronach ulicy jest po k=15 miejsc parkingowych.
Na ile sposobów można zaparkować na nich sześć samochodów?
Odpowiedzi:
| A. 30^2 | B. 25\cdot 26\cdot 27\cdot ...\cdot 30 |
| C. 15^2 | D. 15! |
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20123 |
Podpunkt 11.1 (2 pkt)
Wyznacz wszystkie wartości naturalne n, dla których
liczba \frac{4n+29}{2n+1} jest całkowita.
Podaj największą taką liczbę n.
Odpowiedź:
n_{max}=
(wpisz liczbę całkowitą)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20309 |
Podpunkt 12.1 (2 pkt)
» Oblicz miejsce zerowe funkcji
f(x)=
\begin{cases}
3+2x \text{, dla } x\leqslant 2 \\
x \text{, dla } x > 2
\end{cases}
.
Odpowiedź:
| x= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20722 |
Podpunkt 13.1 (2 pkt)
» Trójkąt na rysunku jest równoramienny o podstawie
AB:
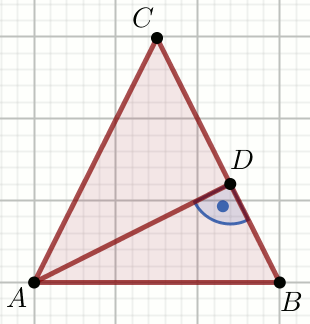

Oblicz |AB|.
Dane
|CD|=\frac{238}{13}=18.307692307692
|DB|=\frac{100}{13}=7.69230769230769
|DB|=\frac{100}{13}=7.69230769230769
Odpowiedź:
| |AB|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20210 |
Podpunkt 14.1 (1 pkt)
« Na trójkącie rozwartokątnym ABC, w którym kąt
przy wierzchołku C jest rozwarty, opisano okrąg
o środku w punkcie S. Kąt środkowy
BSC ma miarę \alpha,
zaś kąt środkowy wypukły ASB miarę
\beta. Oblicz miary kątów trójkąta
ABC.
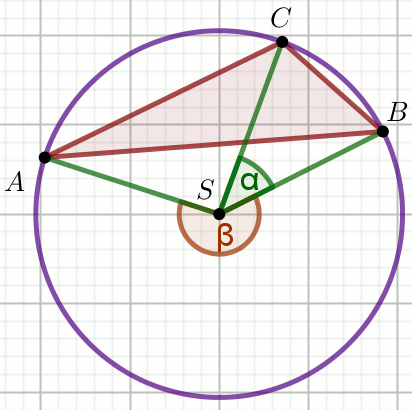

Podaj miarę stopniową najmniejszego z kątów tego trójkąta.
Dane
\alpha=42^{\circ}
\beta=198^{\circ}
\beta=198^{\circ}
Odpowiedź:
\gamma_{min}=
(wpisz liczbę całkowitą)
Podpunkt 14.2 (1 pkt)
Podaj miarę stopniową największego z kątów.
Odpowiedź:
\gamma_{max}=
(wpisz liczbę całkowitą)
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20588 |
Podpunkt 15.1 (2 pkt)
« Prosta o równaniu ax+y+c=0 przechodzi przez punkty
A=\left(3,-1) i B=\left(-3,11\right).
Podaj c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20885 |
Podpunkt 16.1 (2 pkt)
« Dany jest trójkąt ABC, w którym
|AB|=2,
|BC|=2\sqrt{5} i
|AC|=4\sqrt{2}.
Oblicz miarę kąta CAB.
Odpowiedź:
|\sphericalangle CAB|=
(wpisz liczbę całkowitą)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20373 |
Podpunkt 17.1 (1 pkt)
« Rozwiąż równanie
\frac{x}{70-10x}=\frac{10}{x-7}
.
Podaj najmniejsze rozwiązanie tego równania.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 17.2 (1 pkt)
Podaj największe rozwiązanie tego równania.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20817 |
Podpunkt 18.1 (1 pkt)
« Dany jest ciąg arytmetyczny (a_n).
Wyznacz a_1.
Dane
a_{1}+a_{2}=41
a_{7}=48
a_{k}+a_{k+1}=181
a_{7}=48
a_{k}+a_{k+1}=181
Odpowiedź:
a_1=
(wpisz liczbę całkowitą)
Podpunkt 18.2 (1 pkt)
Oblicz k.
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20645 |
Podpunkt 19.1 (1 pkt)
Cyfra setek liczby naturalnej trzycyfrowej należących do zbioru
\{
5,6\}, cyfra dziesiątek do zbioru\{
1,4,9\}, a cyfra jedności do zbioru\{
0,1,7,9\}.
Ile jest takich liczb parzystych?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 19.2 (1 pkt)
Ile jest takich liczb podzielnych przez 3?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20661 |
Podpunkt 20.1 (2 pkt)
» Liczba naturalna 6
cyfrowa jest podzielna przez 4 lub
6.
Ile jest takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)