Podgląd arkusza : lo2@am-3-2023-01-22-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10451 |
Podpunkt 1.1 (1 pkt)
Zbiorem rozwiązań nierówności
x^2+12x\geqslant -36
jest:
Odpowiedzi:
| A. \emptyset | B. \mathbb{R} |
| C. (-\infty, -6\rangle\cup\langle 0,+\infty) | D. \langle 6,+\infty) |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10689 |
Podpunkt 2.1 (1 pkt)
Dziedziną funkcji
f(x)=\frac{x}{\sqrt{16+x^2}}+(2-x)^2
jest:
Odpowiedzi:
| A. (-\infty;-4)\cup(4;+\infty) | B. \mathbb{R} |
| C. \mathbb{R}-\{-4\} | D. \mathbb{R}-\{-4,4\} |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10585 |
Podpunkt 3.1 (1 pkt)
« Przedstawione na rysunku trójkąty są podobne.
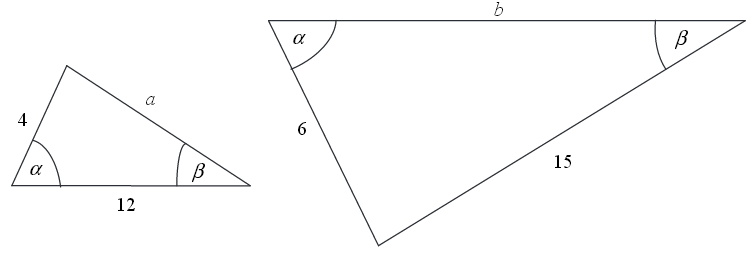

Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10976 |
Podpunkt 4.1 (0.5 pkt)
» Równanie (2x-3)(x+2)=(2x-3)(2x-1) ma dwa
rozwiązania.
Wyznacz najmniejsze rozwiązanie tego równania.
Odpowiedź:
| x_{min}= | |
Podpunkt 4.2 (0.5 pkt)
Wyznacz największe rozwiązanie tego równania.
Odpowiedź:
| x_{max}= | |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10570 |
Podpunkt 5.1 (1 pkt)
Cięciwa okręgu o promieniu 5 cm ma długość
8 cm.
Oblicz odległość środka okręgu od tej cięciwy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11224 |
Podpunkt 6.1 (1 pkt)
Pole powierzchni trójkąta o wierzchołkach K=(0,-5),
L=(5,-10) i M=(5,-2)
jest równe P.
Oblicz długość boku kwadratu o polu powierzchni P.
Odpowiedź:
a=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11679 |
Podpunkt 7.1 (1 pkt)
Wyznacz tę wartość parametru m, dla której wielomian
P(x)=6x^3-8x^2-5x+m-1 dzieli się bez reszty przez
dwumian x-1.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11179 |
Podpunkt 8.1 (1 pkt)
W ciągu geometrycznym (a_n), który zawiera dziewięć
wyrazów, wszystkie wyrazy są dodatnie i znane są dwa wyrazy
a_1 i a_9.
Oblicz a_5.
Dane
a_1=20
a_9=5
a_9=5
Odpowiedź:
a_5=
(wpisz liczbę całkowitą)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11514 |
Podpunkt 9.1 (1 pkt)
«« Czterocyfrowa liczba całkowita dodatnia zapisana jest za pomocą
różnych cyfr, a jej cyfra jedności należy do zbioru
\{0,2,4,5,7\}.
Ile jest takich liczb:
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11265 |
Podpunkt 10.1 (1 pkt)
Na 5 kartkach zapisano wszystkie cyfry ze zbioru
\{1,2,3,...,5\}, na każdej kartce jedną cyfrę.
Losujemy bez zwracania trzy razy po jednej kartce i z wylosowanych cyfr
tworzymy liczbę trzycyfrową.
Ile możemy utworzyć wszystkich takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20112 |
Podpunkt 11.1 (2 pkt)
Rozwiąż równanie \frac{x}{2}-3(x-2)=-5x-6
o niewiadomej x.
Odpowiedź:
| x= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20335 |
Podpunkt 12.1 (2 pkt)
Do wykresu nie stałej funkcji liniowej h(x)=bx+2ab
należy punkt P=(b, 4a^2+2ab) oraz
h(b+2a)\neq 12a^2.
Oblicz wartość ilorazu \frac{a}{b}.
Odpowiedź:
| \frac{a}{b}= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20921 |
Podpunkt 13.1 (1 pkt)
Rozwiąż układ równań:
\begin{cases}
-4\sqrt{3}x+6y=\sqrt{6}\\
-4\sqrt{2}x-3\sqrt{6}y=-3
\end{cases}
.
Podaj x.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.2 (1 pkt)
Podaj y.
Odpowiedź:
| y= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20227 |
Podpunkt 14.1 (2 pkt)
» W okręgu o środku O poprowadzono cięciwę
AB nie przechodzącą przez środek okręgu.
Na cięciwie wybrano punkt C w taki sposób, że
AB nie jest prostopadłe do
CO:
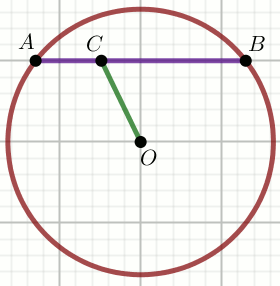

Oblicz długość promienia tego okręgu.
Dane
|CO|=10
|AC|=9
|CB|=21
|AC|=9
|CB|=21
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 15. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30190 |
Podpunkt 15.1 (2 pkt)
«« Punkt A=(0,-4) jest wierzchołkiem trójkąta
ABC, w którym
\overrightarrow{AB}=[7,3] i
\overrightarrow{BC}=[-6,1].
Wyznacz równanie wysokości tego trójkąta przechodzącej przez punkt
C i zapisz je w postaci
ax+y+c=0.
Podaj a.
Odpowiedź:
| a= | |
Podpunkt 15.2 (2 pkt)
Podaj c.
Odpowiedź:
| c= | |
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21033 |
Podpunkt 16.1 (1 pkt)
Dwa boki trójkąta mają długość 11 i 20, a promień
okręgu opisanego na tym trójkącie ma długość \frac{65}{6}. Pole powierzcni
tego trójkąta jest równe 66.
Oblicz długość trzeciego boku tego trójkąta.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
Podpunkt 16.2 (1 pkt)
Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
| r= | |
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20990 |
Podpunkt 17.1 (2 pkt)
Wielomian W(x)=-12x^3-16x^2+3x+4
jest podzielny przez dwumian P(x)=x+\frac{1}{2}, a wynikiem tego dzielenia jest wielomian
Q(x)=ax^2+bx+c.
Wyznacz współczynniki a, b i c.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20509 |
Podpunkt 18.1 (2 pkt)
» Oblicz sumę wszystkich liczb naturalnych trzycyfrowych nieparzystych,
nie większych od 793.
Odpowiedź:
s_{\leqslant k}=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20641 |
Podpunkt 19.1 (2 pkt)
Rozwinięcie dziesiętne k=6 cyfrowej liczby naturalnej rozpoczyna się
cyfrą parzystą, a pozostałe cyfry tego rozwinięcia są nieparzyste.
Ile jest takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20665 |
Podpunkt 20.1 (2 pkt)
«« Z cyfr należących do zbioru \{1,2,3,...,9\} tworzymy
liczby trzycyfrowe o różnych cyfrach, które są mniejsze od
521.
Ile jest takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)