Podgląd arkusza : lo2@am-3-2023-01-22-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10044 |
Podpunkt 1.1 (1 pkt)
Zapisz wyrażenie
\left(3-b\sqrt{3}\right)^3
w najprostszej postaci m+n\sqrt{k}, gdzie
m,n,k\in\mathbb{Z}.
Podaj liczby m, n i k.
Dane
b=4
Odpowiedź:
Wpisz odpowiedź:
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10084 |
Podpunkt 2.1 (1 pkt)
Funkcja f określona jest wzorem:
f(x)=\left\lbrace
\begin{array}{ll}
x-1 & \text{dla }x\leqslant 4\\
-x+7 & \text{dla }x > 4
\end{array}
i ma k miejsc zerowych.
Wyznacz liczbę k.
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10954 |
Podpunkt 3.1 (1 pkt)
Pierwsza rata, która stanowi 26\% ceny roweru
szosowego, jest o 493 zł niższa od raty drugiej,
która stanowi 76\% ceny roweru.
Ile złotych kosztuje rower?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10475 |
Podpunkt 4.1 (1 pkt)
Proste k i l są równoległe.
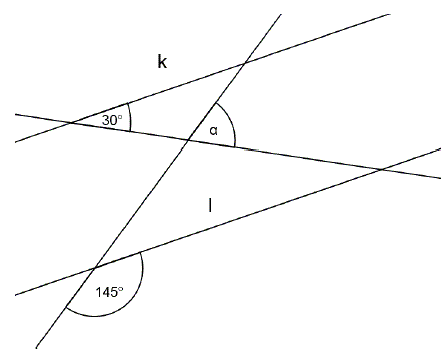

Podaj miarę stopniową kąta \alpha.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11609 |
Podpunkt 5.1 (1 pkt)
Zbiorem wartości funkcji f jest przedział \langle -1,5\rangle.
Zbiorem wartości funkcji określonej wzorem g(x)=f(x-4)-6 jest przedział
\langle c,d\rangle.
Podaj liczby c i d.
Odpowiedzi:
| c | = |
(wpisz liczbę zapisaną dziesiętnie) |
| d | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10973 |
Podpunkt 6.1 (1 pkt)
» Dana jest funkcja
f(x)=
\begin{cases}
-\frac{1}{3}x-1,\qquad x\in(-\infty,-15) \\
x^2-220,\qquad x\in\langle -15,+\infty)
\end{cases}
.
Liczba rozwiązań równania f(x)=5 jest równa:
Odpowiedzi:
| A. 2 | B. 1 |
| C. 3 | D. 0 |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11520 |
Podpunkt 7.1 (1 pkt)
Punkty o współrzędnych A=(-3,1) i
B=(5,9) są symetryczne względem prostej
określonej równaniem:
Odpowiedzi:
| A. y=x+6 | B. y=x+8 |
| C. y=-x+6 | D. y=-x+8 |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11151 |
Podpunkt 8.1 (1 pkt)
« W kinie jest r rzędów krzeseł. Rząd pierwszy
składa się z p krzeseł, a każdy następny rząd
zawiera o k krzeseł więcej niż rząd poprzedni.
Ile jest krzeseł w kinie?
Dane
r=28
p=18
k=11
p=18
k=11
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10234 |
Podpunkt 9.1 (1 pkt)
« Z cyfr zbioru \{0,1,2,4,6,8\} utworzono liczbę
trzycyfrową parzystą o niepowtarzających się cyfrach.
Ile jest takich liczb:
Odpowiedzi:
| A. 88 | B. 84 |
| C. 76 | D. 72 |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11269 |
Podpunkt 10.1 (1 pkt)
« Na ile sposobów k=4 osób może usiąść na
n=7 krzesłach?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20104 |
Podpunkt 11.1 (2 pkt)
Rozwiąż równanie
\frac{x-1}{3}-2(x+3)=\frac{x}{4}-x
o niewiadomej x.
Odpowiedź:
| x= | |
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20276 |
Podpunkt 12.1 (2 pkt)
« O kącie \alpha wiadomo, że jest ostry i
\sin\alpha=\frac{1}{4}.
Oblicz wartość wyrażenia 2\tan^2\alpha+1.
Odpowiedź:
| 2\tan^2\alpha+1= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20765 |
Podpunkt 13.1 (2 pkt)
« Punkt O jest środkiem okręgu. Oblicz pole
powierzchni niebieskiego obszaru:
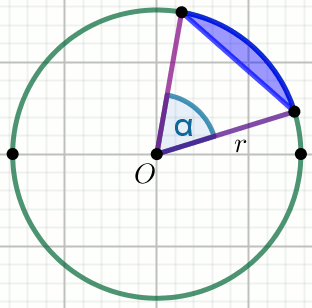

Dane
r=16
\alpha=45^{\circ}
\alpha=45^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30146 |
Podpunkt 14.1 (2 pkt)
« Plac zabaw w kształcie prostokąta miał powierzchnię
p_1 m2. Po przebudowie jego powierzchnia
wzrosła do p_2 m2 i był wówczas o
x metrów dłuższy i y
metrów szerszy. Oblicz wymiary placu po przebudowie.
Podaj najmniejszy możliwy obwód placu po przebudowie.
Dane
p_1=2288
p_2=2916
x=10
y=2
p_2=2916
x=10
y=2
Odpowiedź:
| L_{min}= | |
Podpunkt 14.2 (2 pkt)
Podaj największy możliwy obwód placu po przebudowie.
Odpowiedź:
| L_{max}= | |
| Zadanie 15. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30244 |
Podpunkt 15.1 (2 pkt)
«« Z cyfr należących do zbioru
\{
2,4,5,6,8\} oraz liter należących do zbioru\{
H,K,Z\} utworzono ośmioznakowy numer seryjny.
Ile jest takich numerów, w których cyfry nie powtarzają się i wszystkie występują po literach?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 15.2 (2 pkt)
Ile jest takich numerów seryjnych, jeśli wiadomo, że wszystkie litery występują przed wszystkimi
cyframi i zarówno cyfry jak i litery moga się powtarzać?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 16. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30075 |
Podpunkt 16.1 (2 pkt)
« Rozwiąż równanie
x^2-(a+6)x+\left|x-3-\frac{a}{2}\right|+\frac{1}{4}a^2+3a-3=0
.
Podaj najmniejsze rozwiązanie tego równania.
Dane
a=-1
Odpowiedź:
| x_{min}= | |
Podpunkt 16.2 (2 pkt)
Podaj największe rozwiązanie tego równania.
Odpowiedź:
| x_{max}= | |
| Zadanie 17. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30261 |
Podpunkt 17.1 (2 pkt)
» W prostokącie ABCD dane są:
C=(-2,3),
\overrightarrow{AB}=[4,4] oraz prosta
y=x-1, do której należy wierzchołek
A tego prostokąta. Wyznacz równanie
przekątnej AC:y=cx+d.
Podaj c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
Podpunkt 17.2 (2 pkt)
Podaj d.
Odpowiedź:
d=
(wpisz liczbę całkowitą)
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-21008 |
Podpunkt 18.1 (1 pkt)
Wielomian W(x)=x^3+6x^2+ax+b ma trzy pierwiastki
x_1, x_2 i x_3 takie,
że x_2-x_1=5 i x_3-x_1=7.
Wyznacz najmniejszy i największy pierwiastek tego wielomianu.
Odpowiedzi:
| min | = |
(wpisz liczbę całkowitą) |
| max | = |
(wpisz liczbę całkowitą) |
Podpunkt 18.2 (1 pkt)
Wyznacz wartości parametrów a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20420 |
Podpunkt 19.1 (2 pkt)
» Ze zbioru k znaków losujemy jeden lub dwa
znaki. Możemy w ten sposób uzyskać 841 ciągów jedno
lub dwu wyrazowych, o różnych wyrazach.
Wyznacz k.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 20. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30320 |
Podpunkt 20.1 (4 pkt)
Suma wszystkich cyfr występujących w k=89 znakowym
rozwinięciu dziesiętnym liczby naturalnej jest równa 4.
Ile jest takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)