Podgląd arkusza : lo2@am-3-2023-02-05-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10432 |
Podpunkt 1.1 (1 pkt)
Zapisz wyrażenie
3^{28}+9^{6}-3^{12}+9^{10}-3^{20}+9^{14}+3^{28}
w postaci potęgi o podstawie 3.
Podaj wykładnik tej potęgi.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11592 |
Podpunkt 2.1 (1 pkt)
Wyznacz wartości parametrów m i n tak,
aby pary liczb \left(\frac{51}{4},m+1\right) i
(n+8,1) spełniały równanie
\frac{1}{5}x-\frac{2}{5}y=-\frac{2}{5}.
Podaj liczby m i n.
Odpowiedzi:
| m | = | (dwie liczby całkowite) | |
| n | = | (wpisz liczbę całkowitą) | |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11568 |
Podpunkt 3.1 (0.5 pkt)
W trapezie podstawy mają długość 27 i
60, a wysokość ma długość 11.
Wyznacz odległości punktu przecięcia się przekątynych tego trapezu od jego podstaw.
Podaj krótszą z tych odległości.
Odpowiedź:
| min= | |
Podpunkt 3.2 (0.5 pkt)
Podaj dłuższą z tych odległości.
Odpowiedź:
| max= | |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11022 |
Podpunkt 4.1 (1 pkt)
« Rysunek przedstawia wykres funkcji kwadratowej
h(x)=a(x+b)^2+c.
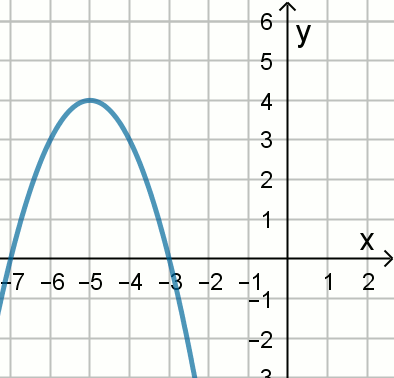

Zatem:
Odpowiedzi:
| A. b=5 | B. b=-5 |
| C. c=-5 | D. c=5 |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10628 |
Podpunkt 5.1 (1 pkt)
« Wyrażenie \sin 46^{\circ} jest równe:
Odpowiedzi:
| A. \cos 44^{\circ} | B. \sin 44^{\circ} |
| C. \tan 44^{\circ} | D. \cos 46^{\circ} |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11249 |
Podpunkt 6.1 (1 pkt)
Dane są współrzędne dwóch kolejnych wierzchołków kwadratu A=\left(-\frac{11}{2},-1\right) i
B=\left(6,\frac{11}{2}\right). Przekątne tego kwadratu mogą się przecinać
w punkcie:
Odpowiedzi:
| A. \left(-3,\frac{23}{3}\right) | B. \left(-\frac{19}{6},\frac{49}{6}\right) |
| C. \left(-\frac{8}{3},8\right) | D. \left(-3,8\right) |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11141 |
Podpunkt 7.1 (1 pkt)
Wyznacz największe rozwiązanie równania
x+a=\frac{b}{x}
.
Dane
a=14
b=-24
b=-24
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11147 |
Podpunkt 8.1 (1 pkt)
Ciąg (c_n) dany jest wzorem
c_n=(n-k)\cdot p dla
n\geqslant 1.
Oblicz S_{20}.
Dane
k=16
p=5
p=5
Odpowiedź:
S_{20}=
(wpisz liczbę całkowitą)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11257 |
Podpunkt 9.1 (1 pkt)
Na płaszczyźnie zaznaczono 8 różnych punktów
zielonych i 11 różnych punktów czerwonych.
Ile istnieje odcinków o końcach w tych punktach takich, że punkty końcowe odcinka mają różne kolory?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11263 |
Podpunkt 10.1 (1 pkt)
« Zamawiając obiad mamy do wyboru 8 różnych surówek,
3 rodzaje kompotu i 3 różne sosy.
Na ile sposobów możemy wybrać składniki jeśli wybierami dwie surówki, jeden kompot i jeden sos?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20859 |
Podpunkt 11.1 (1 pkt)
(1 pkt)
Wykaż, że dla każdych liczb całkowitych x i
y, wyrażenie
40x^2+16y^2+16xy+108x+81
można zapisać w postaci (a_1x+b_1y+c_1)^2+(a_2x+b_2y+c_2)^2, gdzie współczynniki
a_1\text{, }b_1\text{, } c_1\text{, } a_2\text{, } b_2\text{ i } c_2 są liczbami całkowitymi
(niektóre z nich mogą być równe zero).
Podaj mniejszą z liczb a_1 i a_2.
Odpowiedź:
min(a_1,a_2)=
(wpisz liczbę całkowitą)
Podpunkt 11.2 (1 pkt)
(1 pkt)
Podaj większą z liczb b_1 i b_2.
Odpowiedź:
max(b_1,b_2)=
(wpisz liczbę całkowitą)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20309 |
Podpunkt 12.1 (2 pkt)
» Oblicz miejsce zerowe funkcji
f(x)=
\begin{cases}
-1+2x \text{, dla } x\leqslant 2 \\
x \text{, dla } x > 2
\end{cases}
.
Odpowiedź:
| x= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20842 |
Podpunkt 13.1 (1 pkt)
Trójkąt ABC ma obwód równy O.
Trójkąt A_1B_1C_1 jest podobny do trójkąta
ABC w skali k. Znając długości
dwóch jego boków oblicz długości boków trójkąta ABC.
Jaką długość ma najkrótszy bok trójkąta ABC?
Dane
O=42
k=3
|A_1B_1|=33
|A_1C_1|=42
k=3
|A_1B_1|=33
|A_1C_1|=42
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 13.2 (1 pkt)
Jaką długość ma najdłuższy bok trójkąta ABC?
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20390 |
Podpunkt 14.1 (2 pkt)
» Dla jakich wartości parametru m funkcja
y=-x^2+12x+m-a nie ma miejsc zerowych?
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Dane
a=-4
Odpowiedź:
p=
(wpisz liczbę całkowitą)
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20312 |
Podpunkt 15.1 (2 pkt)
« Dana jest prosta k o równaniu
x-10y-8=0 oraz punkt
P=(-10,3). Wyznacz równanie prostej
l równoległej do prostej k
i przechodzącej przez punkt P. Zapisz równanie
prostej l w postaci kierunkowej
y=a_1x+b_1.
Podaj b_1.
Odpowiedź:
| b_1= | |
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20749 |
Podpunkt 16.1 (2 pkt)
« W trójkącie prostokątnym kąt ostry spałnia warunek \cos\alpha=\frac{7}{13},
a promień okręgu opisanego na tym trójkącie ma długość
\frac{65}{6}.
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
P_{\triangle}=
(liczba zapisana dziesiętnie)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20969 |
Podpunkt 17.1 (2 pkt)
« Wielomian
W(x)=x^3-8x^2+mx-1
przy dzieleniu przez dwumian x-3 daje resztę
-\frac{59}{2}.
Oblicz wartość parametru m.
Odpowiedź:
| m= | |
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20517 |
Podpunkt 18.1 (1 pkt)
Ciąg (a-b,a^2-2,k-b) jest ciągiem
atytmetycznym i geometrycznym. Wyznacz a i
b.
Podaj a.
Dane
k=4
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 18.2 (1 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20644 |
Podpunkt 19.1 (1 pkt)
Z cyfr należących do zbioru
\{
3,5,9\} oraz liter należących do zbioru\{
B,I\}, utworzono kod składający się z 5 znaków.
Ile jest takich kodów, w których znaki nie powtarzają się?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 19.2 (1 pkt)
Ile jest takich kodów, w których występują wszystkie cyfry, a litery mogą
się powtarzać i występują przed cyframi?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20666 |
Podpunkt 20.1 (2 pkt)
« Ile jest liczb naturalnych 3 cyfrowych o różnych
cyfrach, które są podzielne przez 25?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)