Podgląd arkusza : lo2@am-3-2023-03-05-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10140 |
Podpunkt 1.1 (1 pkt)
Pierwsza rata, która stanowi 12\% ceny roweru,
jest równa 477 zł. Wynika z tego, że rower
kosztuje .......... zł.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10798 |
Podpunkt 2.1 (1 pkt)
Trójkąt o bokach długości 5,
2p+25, p+11 jest
równoramienny.
Wyznacz p.
Odpowiedź:
p=
(wpisz liczbę całkowitą)
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10596 |
Podpunkt 3.1 (1 pkt)
« Odcinki DE i AB
są równoległe, przy czym
|DE|=\frac{1}{6} i
|AB|=\frac{11}{12}:
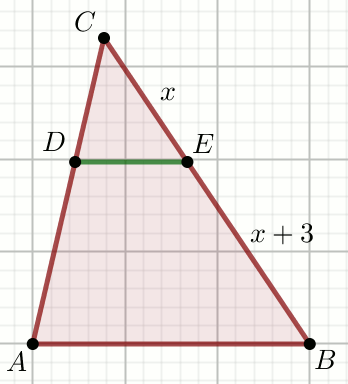

Oblicz x.
Odpowiedź:
| x= | |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10965 |
Podpunkt 4.1 (1 pkt)
Wskaż te nierówności, których rozwiązaniem jest zbiór \mathbb{R}:
Odpowiedzi:
| T/N : x^2+x-4 \geqslant 0 | T/N : x^2+\frac{1}{2}x+\frac{1}{16} > 0 |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10530 |
Podpunkt 5.1 (1 pkt)
Dany jest okrąg o środku w punkcie S, w którym
a=54^{\circ}:
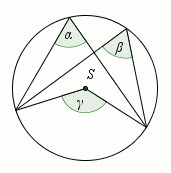

Oblicz sumę miar stopniowych kątów \beta i \gamma.
Odpowiedź:
\beta+\gamma=
(wpisz liczbę całkowitą)
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11600 |
Podpunkt 6.1 (1 pkt)
« Punkt O jest środkiem koła na rysunku, a promień r tego
koła ma długość 20. Kąt środkowy koła \alpha
oparty jest na łuku o długości 18\pi:
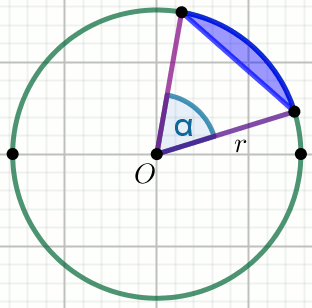

Oblicz pole powierzchni zaznaczonego na rysunku odcinka koła.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11673 |
Podpunkt 7.1 (1 pkt)
Iloczyn wyrażenia 2x-5 przez wyrażenie
-4x^2-10x-25
jest równy
ax^3+bx+c, gdzie
a,b,c\in\mathbb{Z}.
Podaj liczby a, b i c.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11148 |
Podpunkt 8.1 (1 pkt)
« W ciągu arytmetycznym (a_n) dane są:
a_k=18 i a_{k+7}=46.
Wówczas a_1+r jest równe:
Odpowiedź:
a_1+r=
(wpisz liczbę całkowitą)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11285 |
Podpunkt 9.1 (1 pkt)
Liczba naturalna składa się czterech cyfr, spośród których tylko jedna jest
cyfrą nieparzystą.
Ile jest takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11266 |
Podpunkt 10.1 (1 pkt)
Święty Mikołaj zapakował 5 różnych prezentów
do 5 różnych mikołajowych worków, tak aby żaden worek nie był pusty.
Na ile sposóbów mógł to zrobić?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20080 |
Podpunkt 11.1 (2 pkt)
Rozwiąż równanie z niewiadomą x:
\frac{x-3}{3}=\frac{x+8}{2}
.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20840 |
Podpunkt 12.1 (1 pkt)
« Funkcja liniowa f określona wzorem
f(x)=mx+n wartości nieujemne przyjmuje tylko
w przedziale (-\infty, 2\rangle oraz zachodzi
warunek f(-1)=18. Wyznacz wartości współczynników
m i n.
Podaj m.
Odpowiedź:
| m= | |
Podpunkt 12.2 (1 pkt)
Podaj n.
Odpowiedź:
| n= | |
| Zadanie 13. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20777 |
Podpunkt 13.1 (0.25 pkt)
« Punkty A=(-1,1),
B=(3,4) i C=(4,7)
są trzema kolejnymi wierzchołkami równoległoboku
ABCD (odwrotnie do wskazówek zegara).
Wyznacz współrzedne punktu S=(x_S, y_S),
w którym przecinają się przekątne tego równoległoboku.
Podaj x_S.
Odpowiedź:
| x_S= | |
Podpunkt 13.2 (0.25 pkt)
Podaj y_S.
Odpowiedź:
y_S=
(wpisz liczbę całkowitą)
Podpunkt 13.3 (0.5 pkt)
Oblicz |BD|.
Odpowiedź:
|BD|=
(wpisz liczbę całkowitą)
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20366 |
Podpunkt 14.1 (1 pkt)
Funkcja kwadratowa jest określona wzorem
f(x)=ax^2+bx+c.
Oblicz najmniejszą wartość funkcji f w przedziale \langle p,q\rangle.
Dane
a=1
b=2
c=-4
p=-2
q=3
b=2
c=-4
p=-2
q=3
Odpowiedź:
f_{min}(x)=
(wpisz liczbę całkowitą)
Podpunkt 14.2 (1 pkt)
Dla jakiego x funkcja f
osiąga minimum?
Odpowiedź:
x=
(wpisz liczbę całkowitą)
| Zadanie 15. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30187 |
Podpunkt 15.1 (2 pkt)
«« Punkty K=(-1,0) oraz L
są środkami boków odpowiednio AC i
BC trójkata ABC.
Wiadomo, że \overrightarrow{AK}=[1,6] oraz
\overrightarrow{KL}=[8,4]. Wyznacz równanie
boku AB tego trójkąta i zapisz go w postaci
kierunkowej y=ax+b.
Podaj a.
Odpowiedź:
| a= | |
Podpunkt 15.2 (2 pkt)
Podaj b.
Odpowiedź:
| b= | |
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20764 |
Podpunkt 16.1 (2 pkt)
» Punkt O jest środkiem okręgu, z którego
wycięto wycinek kołowy:
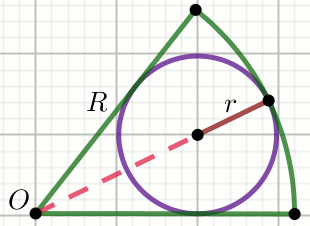

Oblicz pole powierzchni tego wycinka.
Dane
r=3
R=9
R=9
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20811 |
Podpunkt 17.1 (1 pkt)
(1 pkt) Rozwiąż równanie
\frac{(x^3+p)(2x^2+bx+c)}{x^2+mx+n}=0
.
Podaj największe z rozwiązań tego równania.
Dane
p=8
b=-2
c=-24
m=5
n=6
b=-2
c=-24
m=5
n=6
Odpowiedź:
max=
(wpisz liczbę całkowitą)
Podpunkt 17.2 (1 pkt)
(1 pkt) Podaj sumę wszystkich ujemnych rozwiązań tego równania.
Odpowiedź:
suma=
(wpisz liczbę całkowitą)
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20503 |
Podpunkt 18.1 (2 pkt)
«« Dany jest ciąg arytmetyczny (-20, x-3, y, -5).
Oblicz x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20645 |
Podpunkt 19.1 (1 pkt)
Cyfra setek liczby naturalnej trzycyfrowej należących do zbioru
\{
3,4\}, cyfra dziesiątek do zbioru\{
1,2,5\}, a cyfra jedności do zbioru\{
0,3,7,9\}.
Ile jest takich liczb parzystych?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 19.2 (1 pkt)
Ile jest takich liczb podzielnych przez 3?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20656 |
Podpunkt 20.1 (2 pkt)
« W liczbie 3 cyfrowej cyfra
9 występuje co najwyżej raz. Ile jest takich
liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)