Podgląd arkusza : lo2@am-3-2023-03-19-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10093 |
Podpunkt 1.1 (1 pkt)
» Dany jest trójkąt o bokach długości a,
b, c.
Stosunek a:b:c jest równy
5:15:8.
Które zdanie jest prawdziwe:
Odpowiedzi:
| A. liczba c jest o 60.0% mniejsza od liczby a+b | B. liczba c jest o 65.0% mniejsza od liczby a+b |
| C. liczba a stanowi 26.7% liczby b+c | D. liczba a stanowi 22.9% liczby a+b+c |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10911 |
Podpunkt 2.1 (1 pkt)
Wskaż prostą równoległą do osi Ox:
Odpowiedzi:
| A. 4x=2y | B. 4x=0 |
| C. x-4=y | D. 4x=2 |
| E. 2x+4=0 | F. 2y+4=0 |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10649 |
Podpunkt 3.1 (1 pkt)
« W trójkącie prostokątnym najdłuższy bok ma długość
34, a najkrótszy 16.
Oblicz tangens największego kąta ostrego tego trójkąta.
Odpowiedź:
| \tan\alpha= | |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11005 |
Podpunkt 4.1 (0.2 pkt)
« Funkcja y=-(x-3)^2+7 jest rosnąca w pewnym
przedziale liczbowym.
Przedział ten ma postać:
Odpowiedzi:
| A. (p,+\infty) | B. (p,q) |
| C. (-\infty,p) | D. (-\infty,p\rangle |
| E. \langle p,+\infty) | F. \langle p,q\rangle |
Podpunkt 4.2 (0.8 pkt)
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10519 |
Podpunkt 5.1 (1 pkt)
Na okręgu o środku O zaznaczono k=36
wierzchołków wielokąta foremnego. Spośród nich wybrano trzy kolejne i narysowano kąt
jak na rysunku:
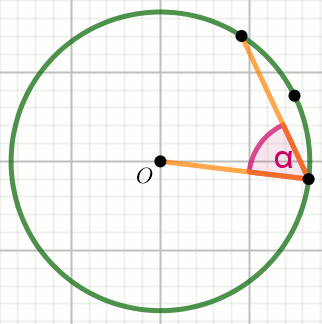

Wyznacz miarę stopniową kąta \alpha.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11225 |
Podpunkt 6.1 (1 pkt)
« W kwadracie o wierzchołkach ABCD punkty
K=(2,5) i L=(6,1) są
środkami boków odpowiednio AB i
BC. Zapisz długość przekątnej tego kwadratu w najprostszej postaci
a\sqrt{b}, gdzie a,b\in\mathbb{N}.
Podaj liczby a i b.
Odpowiedź:
d=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11556 |
Podpunkt 7.1 (1 pkt)
Suma wielomianów W(x)=-2x^3+5x^2-3 oraz
P(x)=2x^3+12x wynosi:
Odpowiedzi:
| A. 4x^3+5x^2+12x-3 | B. 4x^6+5x^2+12x-3 |
| C. 4x^3+12x^2-3 | D. 5x^2+12x-3 |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11387 |
Podpunkt 8.1 (1 pkt)
« Oceń, które z podanych ciągów są malejące?
Odpowiedzi:
| T/N : a_n=\frac{1}{1-4n} | T/N : a_n=1-\frac{4}{n+1} |
| T/N : a_n=\frac{n+4}{n+1} |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11272 |
Podpunkt 9.1 (1 pkt)
« Liczba dwucyfrowa jest większa od 41 i składa
się z różnych cyfr.
Ile jest takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11299 |
Podpunkt 10.1 (1 pkt)
Na zebranie zarządu spółki przyszło 15 akcjonariuszy
i każdy z nich przywitał się ze wszystkimi pozostałymi uczestnikami
spotkania.
Ile było wszystkich powitań.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20045 |
Podpunkt 11.1 (2 pkt)
» Rozwiąż nierówność z niewiadomą x:
\frac{2x-6}{2}-1 \lessdot \frac{2x-a}{3}-4
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Dane
a=4
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20306 |
Podpunkt 12.1 (1 pkt)
« Dane są punkty A=(-10, 43) i
B=(-2, -5). Wyznacz równanie prostej
AB.
Podaj współczynnik kierunkowy tej prostej.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 12.2 (1 pkt)
Wyznacz odciętą punktu przecięcia prostej AB
z osią Ox.
Odpowiedź:
| x_0= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20235 |
Podpunkt 13.1 (2 pkt)
» Korzystając z danych i rysunku oblicz długość zielonego odcinka:
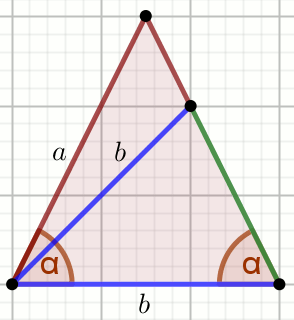

Dane
a=20
b=13
b=13
Odpowiedź:
| d= | |
| Zadanie 14. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20930 |
Podpunkt 14.1 (1 pkt)
Funkcja kwadratowa f określona wzorem
f(x)=a(x-p)^2+q dla argumentu
7 osiąga wartość największą równą
10. Wiedząc, że do jej wykresu należy punkt
należy punkt A=(5,7), wyznacz wzór tej funkcji.
Podaj współczynnik a.
Odpowiedź:
| a= | |
Podpunkt 14.2 (1 pkt)
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20590 |
Podpunkt 15.1 (1 pkt)
» Prosta o równaniu y=ax+b przechodzi przez punkt
P=(1+\sqrt{6},-2+2\sqrt{2}) i jest nachylona do osi
Ox pod kątem o mierze
150^{\circ}.
Podaj a.
Odpowiedź:
| a= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 15.2 (1 pkt)
Podaj b.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20746 |
Podpunkt 16.1 (1 pkt)
« Jeden z kątów trójkąta równoramiennego ma miarę
\alpha taką, że \cos\alpha=-\frac{\sqrt{3}}{2}
a pole powierzchni tego trójkąta jest równe 784\sqrt{3}.
Oblicz \alpha.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
Podpunkt 16.2 (1 pkt)
Oblicz długość ramienia tego trójkąta.
Odpowiedź:
c=
(liczba zapisana dziesiętnie)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20830 |
Podpunkt 17.1 (2 pkt)
Zapisz wyrażenie \frac{3}{x-3}-\frac{x}{x+1}
w postaci ilorazu dwóch wielomianów.
Podaj wartość bezwzględną z sumy współczynników wielomianu występującego w liczniku tego ilorazu.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20505 |
Podpunkt 18.1 (2 pkt)
Na okręgu o promieniu długości r opisano
trójkąt o bokach długości
a\leqslant b\leqslant c, które są kolejnymi
wyrazami ciągu arytmetycznego.
Oblicz stosunek wysokości opuszczonej na bok długości b, do długości promienia okręgu r.
Odpowiedź:
\frac{h}{r}=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20652 |
Podpunkt 19.1 (2 pkt)
Na ile sposobów można ustawić w szereg m=6 chłopców
i n=7 dziewcząt tak, aby osoby tej samej płci nie
stały obok siebie?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20655 |
Podpunkt 20.1 (2 pkt)
W liczbie 4 cyfrowej cyfra
0 występuje co najwyżej raz. Ile jest takich
liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)