Podgląd arkusza : lo2@am-3-2023-04-16-pp
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10445 |
Podpunkt 1.1 (1 pkt)
Zapisz wyrażenie
\left(3-\sqrt{2}\right)^2+2\left(5-\sqrt{2}\right)
w najprostszej postaci m+n\sqrt{k}, gdzie
m,n,k\in\mathbb{Z}.
Odpowiedź:
m+n\sqrt{k}=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10944 |
Podpunkt 2.1 (1 pkt)
Funkcja f jest określona wzorem
f(x)=-2x-\frac{1}{2} dla każdej liczby z przedziału
\langle -3,1\rangle. Zbiorem wartości tej funkcji jest przedział
\langle p, q\rangle.
Podaj liczby p i q.
Odpowiedzi:
| p | = | (dwie liczby całkowite) | |
| q | = | (dwie liczby całkowite) | |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11570 |
Podpunkt 3.1 (1 pkt)
Wykres funkcji g(x)=|x+4|-4
można otrzymać przesuwając wykres funkcji f(x)=|x|
o wektor \vec{u}=[p,q].
Podaj współrzędne wektora p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę zapisaną dziesiętnie) |
| q | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10990 |
Podpunkt 4.1 (1 pkt)
Funkcja f(x)=x^2-10x+25
dla argumentu \sqrt{5} przyjmuje wartość
\left(......\cdot\sqrt{5}-5\right)^2.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10506 |
Podpunkt 5.1 (1 pkt)
Punkt O jest środkiem a prosta jest styczną
to tego okręgu, przy czym
\alpha=60^{\circ}:
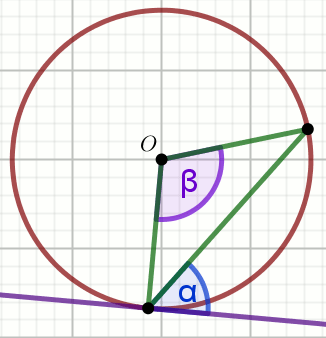

Wyznacz miarę stopniową kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11416 |
Podpunkt 6.1 (1 pkt)
« Do prostej o równaniu y=ax+b należy punkt
A=\left(\frac{1}{2}, -2\right) i prosta ta jest
prostopadła do prostej o równaniu
y=-4x-1.
Wyznacz b.
Odpowiedź:
| b= | |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11140 |
Podpunkt 7.1 (1 pkt)
« Mianownik ułamka jest o 2 większy od licznika
tego ułamka. Gdyby licznik i mianownik zwiększyć o 7,
to ułamek byłby równy \frac{14}{15}.
Oblicz sumę licznika i mianownika tego ułamka.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11158 |
Podpunkt 8.1 (1 pkt)
« Ciąg liczbowy (a_n) określony jest wzorem
a_n=\frac{an^2+bn+c}{n^2-d}, a liczby
p i q są odpowiednio najmniejszym
i największym numerem wyrazów ciągu, które są równe 0.
Podaj liczby p i q.
Dane
a=2
b=-16
c=24
d=-4
b=-16
c=24
d=-4
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11286 |
Podpunkt 9.1 (1 pkt)
Cyfry liczby naturalnej czterocyfrowej abcd
spełniają warunki: d-a=3 oraz
a \lessdot b \lessdot c \lessdot d.
Ile jest takich liczb?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11269 |
Podpunkt 10.1 (1 pkt)
« Na ile sposobów k=4 osób może usiąść na
n=6 krzesłach?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20132 |
Podpunkt 11.1 (2 pkt)
Oblicz wartość wyrażenia
w=a^{\log_{b}{5}}+c^{\log_{d}{e}}
.
Dane
a=64
b=4
c=\frac{1}{4}=0.25000000000000
d=4
e=3
b=4
c=\frac{1}{4}=0.25000000000000
d=4
e=3
Odpowiedź:
| w= | |
| Zadanie 12. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30056 |
Podpunkt 12.1 (4 pkt)
« Z miejscowości A wyjechał autobus osobowy i dotarł
do miejscowości B po
t godzinach jazdy. Godzinę póżniej od autobusu
osobowego na tę samą trasę wyjechał autobus pospieszny i dotarł do miejscowości
B o godzinę wcześniej niż autobus osobowy.
Po ilu godzinach swojej jazdy autobus pospieszny wyprzedził autobus osobowy?
Dane
t=6
Odpowiedź:
| t\ [h]= | |
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20723 |
Podpunkt 13.1 (2 pkt)
« Dane są punkty na okręgu
takie, że |AP|=\frac{3}{2},
|PB|=\frac{4}{5} i
|CP|=\frac{3}{5}:
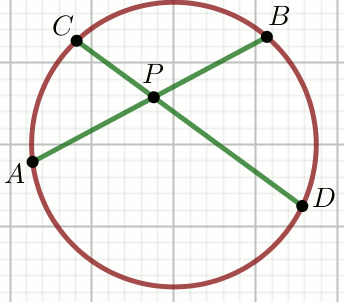

Oblicz |PD|.
Odpowiedź:
| |PD|= | |
| Zadanie 14. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30078 |
Podpunkt 14.1 (2 pkt)
Dana jest funkcja f(x)=(ax+b)(cx+d). Oblicz
najmniejszą i największą wartość tej funkcji w przedziale
\langle p,q\rangle.
Podaj wartość najmniejszą w tym przedziale.
Dane
a=-2
b=-4
c=1
d=5
p=-5
q=1
b=-4
c=1
d=5
p=-5
q=1
Odpowiedź:
| min= | |
Podpunkt 14.2 (2 pkt)
Podaj wartość największą w tym przedziale.
Odpowiedź:
| max= | |
| Zadanie 15. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20331 |
Podpunkt 15.1 (2 pkt)
« Wykres funkcji liniowej y=ax+b jest
nachylony do osi Ox pod kątem
135^{\circ} i przechodzi przez punkt
A=(5,-1).
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20753 |
Podpunkt 16.1 (2 pkt)
» Promień okręgu opisanego na trójkącie prostokątnym jest równy
R, a promień okręgu wpisanego w ten trójkąt -
r.
Oblicz pole powierzchni tego trójkąta.
Dane
R=65
r=14=14.00000000000000
r=14=14.00000000000000
Odpowiedź:
P_{\triangle}=
(wpisz liczbę całkowitą)
| Zadanie 17. (3 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20979 |
Podpunkt 17.1 (1 pkt)
Rozwiąż równanie -x^3-5x^2+28x+140=0.
Podaj rozwiązanie całkowite tego równania.
Odpowiedź:
x_{\mathbb{Z}}=
(wpisz liczbę całkowitą)
Podpunkt 17.2 (1 pkt)
Podaj najmniejsze rozwiązanie tego równania, które nie jest liczbą całkowitą.
Odpowiedź:
min_{\not\in\mathbb{Z}}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 17.3 (1 pkt)
Podaj największe rozwiązanie tego równania, które nie jest liczbą całkowitą.
Odpowiedź:
max_{\not\in\mathbb{Z}}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 18. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30166 |
Podpunkt 18.1 (2 pkt)
Suma pierwszych pięciu wyrazów ciągu arytmetycznego
(a_n) wynosi s1,
a suma a_6+a_7+a_8+...+a_{12} wynosi
s2.
Oblicz a_1.
Dane
s1=905
s2=301
s2=301
Odpowiedź:
a_{1}=
(wpisz liczbę całkowitą)
Podpunkt 18.2 (2 pkt)
Oblicz różnicę tego ciągu.
Odpowiedź:
r=
(wpisz liczbę całkowitą)
| Zadanie 19. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20707 |
Podpunkt 19.1 (2 pkt)
Z cyfr należących do zbioru \{1,2,3,...,6\} tworzymy
liczby pięciocyfrowe parzyste o różnych cyfrach.
Ile różnych takich liczb możemy utworzyć?
Odpowiedź:
ilosc\ liczb=
(wpisz liczbę całkowitą)
| Zadanie 20. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30247 |
Podpunkt 20.1 (2 pkt)
« W rozwinięciu dziesiętnym liczby naturalnej 3
cyfrowej występują tylko cyfry należące do zbioru
\{0,1,2,3,4,5,6\}.
Ile takich liczb parzystych można utworzyć?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 20.2 (2 pkt)
Ile wśród nich jest podzielnych przez 4?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)