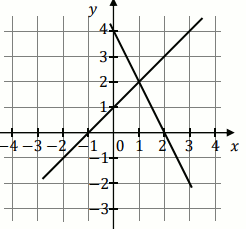Podgląd arkusza : lo2@cke-2021-05-pp
Zadanie 1. 1 pkt ⋅ Numer: pp-12052 ⋅ Poprawnie: 313/327 [95%]
Rozwiąż
Podpunkt 1.1 (1 pkt)
Liczba
100^{8}\cdot (0,1)^{10} jest równa:
Odpowiedzi:
A. 10^{9}
B. 10^{10}
C. 10^{16}
D. 10^{12}
E. 10^{6}
F. 10^{4}
Zadanie 2. 1 pkt ⋅ Numer: pp-12053 ⋅ Poprawnie: 120/126 [95%]
Rozwiąż
Podpunkt 2.1 (1 pkt)
Liczba
152 stanowi
160\%
liczby
c .
Wtedy liczba c jest równa:
Odpowiedzi:
A. 96
B. 91
C. 100
D. 101
E. 95
F. 102
Zadanie 3. 1 pkt ⋅ Numer: pp-12054 ⋅ Poprawnie: 120/137 [87%]
Rozwiąż
Podpunkt 3.1 (1 pkt)
Rozważamy przedziały liczbowe
(-\infty, 9) i
[-1+\infty) .
Ile jest wszystkich liczb całkowitych, które należą jednocześnie do obu
rozważanych przedziałów?
Odpowiedzi:
A. 5
B. 14
C. 10
D. 13
E. 8
F. 11
Zadanie 4. 1 pkt ⋅ Numer: pp-12055 ⋅ Poprawnie: 287/289 [99%]
Rozwiąż
Podpunkt 4.1 (1 pkt)
Liczba
12\log_{5}{\sqrt{5}}+\log_{5}{5^{9}} jest równa:
Odpowiedzi:
A. 15
B. 18
C. 20
D. 12
E. 11
F. 17
Zadanie 5. 1 pkt ⋅ Numer: pp-12056 ⋅ Poprawnie: 308/361 [85%]
Rozwiąż
Podpunkt 5.1 (1 pkt)
Różnica
0,(6)-\frac{19}{22} jest równa:
Odpowiedzi:
A. -\frac{13}{110}
B. -\frac{13}{132}
C. -\frac{13}{66}
D. -\frac{13}{99}
E. -\frac{13}{88}
F. -\frac{13}{33}
Zadanie 6. 1 pkt ⋅ Numer: pp-12057 ⋅ Poprawnie: 36/46 [78%]
Rozwiąż
Podpunkt 6.1 (1 pkt)
Zbiorem wszystkich rozwiązań nierówności
\frac{14-x}{2}-14x\geqslant 1 jest:
Odpowiedzi:
A. \left[\frac{12}{29},+\infty\right)
B. \left(-\infty,\frac{18}{29}\right]
C. \left(-\infty,\frac{48}{145}\right]
D. \left(-\infty,\frac{12}{29}\right)
E. \left(-\infty,\frac{24}{29}\right]
F. \left[\frac{12}{29},+\infty\right)
Zadanie 7. 1 pkt ⋅ Numer: pp-12058 ⋅ Poprawnie: 92/184 [50%]
Rozwiąż
Podpunkt 7.1 (1 pkt)
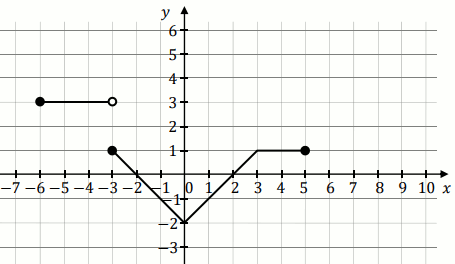
Na poniższym rysunku przedstawiono wykres funkcji
f określonej w zbiorze
[-6,5] .
Funkcja
g jest określona wzorem
g(x)=f(x)-2 .
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
T/N : funkcje f i g mają taki sam zbiór wartości
T/N : punkt P=(-3,1) należy do wykresów obu funkcji
T/N : funkcje f i g mają takie same miejsca zerowe
Zadanie 8. 1 pkt ⋅ Numer: pp-12059 ⋅ Poprawnie: 125/114 [109%]
Rozwiąż
Podpunkt 8.1 (1 pkt)
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów
równań.
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku:
Odpowiedzi:
A. \begin{cases}y=x-1\\y=-2x-4\end{cases}
B. \begin{cases}y=x+1\\y=2x+4\end{cases}
C. \begin{cases}y=x+1\\y=2x-4\end{cases}
D. \begin{cases}y=x-1\\y=2x+4\end{cases}
E. \begin{cases}y=x+1\\y=-2x+4\end{cases}
F. \begin{cases}y=x-1\\y=-2x+4\end{cases}
Zadanie 9. 1 pkt ⋅ Numer: pp-12060 ⋅ Poprawnie: 122/128 [95%]
Rozwiąż
Podpunkt 9.1 (1 pkt)
Proste o równaniach
y=3x-8 oraz
y=\frac{m+5}{2}x+4 są równoległe, gdy
m jest równe:
Odpowiedzi:
A. -5
B. 9
C. -7
D. 1
E. -3
F. 4
G. -4
H. -6
Zadanie 10. 1 pkt ⋅ Numer: pp-12061 ⋅ Poprawnie: 111/167 [66%]
Rozwiąż
Podpunkt 10.1 (1 pkt)
Funkcja
f jest określona wzorem
f(x)=\frac{(x+5)^2}{2x+8}
dla każdej liczby rzeczywistej
x\neq 1 .
Wtedy dla argumentu x=\sqrt{3}-6 wartość funkcji
f jest równa:
Odpowiedzi:
A. \frac{1}{\sqrt{3}}
B. \frac{1}{\sqrt{3}+4}
C. \frac{1}{\sqrt{3}+3}
D. \sqrt{3}+5
E. -1
F. 1
Zadanie 11. 1 pkt ⋅ Numer: pp-12062 ⋅ Poprawnie: 119/167 [71%]
Rozwiąż
Podpunkt 11.1 (1 pkt)
Do wykresu funkcji
f określonej dla każdej liczby rzeczywistej
x wzorem
f(x)=3^x-8 należy
punkt o współrzędnych:
Odpowiedzi:
A. (3,22)
B. (2,3)
C. (0,-4)
D. (3,18)
E. (4,76)
F. (1,-5)
Zadanie 12. 1 pkt ⋅ Numer: pp-12063 ⋅ Poprawnie: 100/111 [90%]
Rozwiąż
Podpunkt 12.1 (1 pkt)
Funkcja kwadratowa
f określona wzorem
f(x)=3(x+1)(x-7) jest malejąca
w przedziale:
Odpowiedzi:
A. \left\langle 7,+\infty)
B. \left(-\infty, 3\rangle
C. \left\langle 3,+\infty)
D. \left(-\infty, 7\rangle
Zadanie 13. 1 pkt ⋅ Numer: pp-12064 ⋅ Poprawnie: 106/120 [88%]
Rozwiąż
Podpunkt 13.1 (1 pkt)
Trzywyrzowy ciąg
\left(60,3x,\frac{12}{5}\right)
jest geometryczny i wszystkie jego wyrazy są dodatnie.
Wynika z tego, że x jest równe:
Odpowiedzi:
A. 4
B. 1
C. \frac{8}{3}
D. 6
E. 8
F. 2
Zadanie 14. 1 pkt ⋅ Numer: pp-12065 ⋅ Poprawnie: 116/131 [88%]
Rozwiąż
Podpunkt 14.1 (1 pkt)
Ciąg
(b_n) jest określony wzorem
b_n=5n^2-66n dla każdej liczby naturalnej
n\geqslant 1 .
Liczba niedodatnich wyrazów ciągu b_n jest równa:
Odpowiedzi:
A. 23
B. 9
C. 25
D. 11
E. 14
F. 7
G. 13
H. 19
Zadanie 15. 1 pkt ⋅ Numer: pp-12066 ⋅ Poprawnie: 203/216 [93%]
Rozwiąż
Podpunkt 15.1 (1 pkt)
Ciąg arytmetyczny
(a_n) jest określony dla każdej liczby
naturalnej
n\geqslant 1 . Piąty i siódmy wyraz tego ciągu
spełniają warunek
a_5+a_7=196 .
Wtedy szósty wyraz tego ciągu jest równy:
Odpowiedzi:
A. 111
B. 102
C. 99
D. 98
E. 108
F. 78
G. 103
H. 82
Zadanie 16. 1 pkt ⋅ Numer: pp-12067 ⋅ Poprawnie: 48/56 [85%]
Rozwiąż
Podpunkt 16.1 (1 pkt)
Dla każdego kąta ostrego
\alpha iloczyn
\frac{1-\sin^2\alpha}{\cos\alpha}\cdot\frac{\sin\alpha}{1-\cos^2\alpha}
jest równy:
Odpowiedzi:
A. \cos\alpha
B. \frac{1}{\sin\alpha\cdot\cos\alpha}
C. \sin\alpha\cdot\cos\alpha
D. \frac{\cos\alpha}{\sin\alpha}
E. \sin^2\alpha
F. \cos^2\alpha
Zadanie 17. 1 pkt ⋅ Numer: pp-12068 ⋅ Poprawnie: 61/75 [81%]
Rozwiąż
Podpunkt 17.1 (1 pkt)
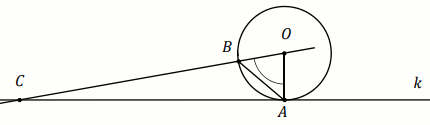
Prosta
k jest styczna w punkcie
A
do okręgu o środku
O . Punkt
B leży na
tym okręgu i miara kąta
AOB jest równa
86^{}\circ{ . Przez punkty
O i
B poprowadzono prostą, która przecina prostą
k w punkcie
C (zobacz rysunek).
Miara kąta BAC jest równa:
Odpowiedzi:
A. 43
B. 42
C. 39
D. 50
E. 53
F. 35
G. 47
H. 37
Zadanie 18. 1 pkt ⋅ Numer: pp-12069 ⋅ Poprawnie: 74/113 [65%]
Rozwiąż
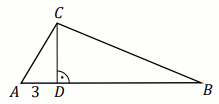
Podpunkt 18.1 (1 pkt)
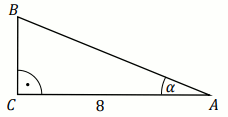
Przyprostokątna
AC trójkąta prostokątnego
ABC
ma długość
8 oraz
\tan\alpha=\frac{9}{2}
(zobacz rysunek).
Pole tego trójkąta jest równe:
Odpowiedzi:
A. 216
B. 144
C. 360
D. 240
E. 72
F. \frac{576}{7}
G. 36
H. 192
Zadanie 19. 1 pkt ⋅ Numer: pp-12070 ⋅ Poprawnie: 69/93 [74%]
Rozwiąż
Podpunkt 19.1 (1 pkt)
Pole pewnego trójkąta równobocznego jest równe
\frac{49\sqrt{3}}{100} .
Obwód tego trójkąta jest równy:
Odpowiedzi:
A. \frac{21\sqrt{3}}{10}
B. \frac{131}{30}
C. \frac{21}{5}
D. \frac{79}{20}
E. \frac{23}{5}
F. \frac{26}{5}
G. \frac{157}{35}
H. \frac{47}{10}
Zadanie 20. 1 pkt ⋅ Numer: pp-12071 ⋅ Poprawnie: 64/93 [68%]
Rozwiąż
Podpunkt 20.1 (1 pkt)
W trójkącie
ABC bok
BC ma długość
45 , a wysokość
CD tego trójkąta
dzieli bok
AB na odcinki o długościach
|AD|=3 i
|BD|=36 (zobacz rysunek).
Długość boku AC jest równa:
Odpowiedzi:
A. \frac{9\sqrt{82}}{8}
B. 3\sqrt{82}
C. \frac{369}{2}
D. 4\sqrt{82}
E. \frac{3\sqrt{82}}{2}
F. 9\sqrt{82}
Zadanie 21. 1 pkt ⋅ Numer: pp-12072 ⋅ Poprawnie: 26/45 [57%]
Rozwiąż
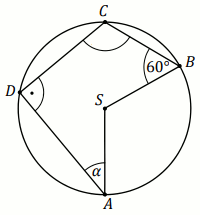
Podpunkt 21.1 (1 pkt)
Punkty
A ,
B ,
C
i
D leżą na okręgu o środku
S . Miary kątów
SBC ,
BCD ,
CDA
są równe odpowiednio:
60^{\circ} ,
124^{\circ} ,
90^{\circ} (zobacz rysunek).
Wynika z tego, że miara \alpha jest równa:
Odpowiedzi:
A. 31^{\circ}
B. 32^{\circ}
C. 28^{\circ}
D. 23^{\circ}
E. 29^{\circ}
F. 26^{\circ}
G. 24^{\circ}
H. 30^{\circ}
Zadanie 22. 1 pkt ⋅ Numer: pp-12073 ⋅ Poprawnie: 36/45 [80%]
Rozwiąż
Podpunkt 22.1 (1 pkt)
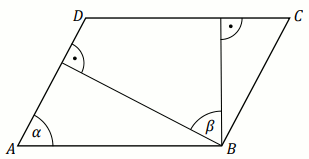
W równoległoboku
ABCD , przedstawionym na rysunku, kąt
\alpha ma miarę
84^{\circ} .
Wtedy kąt \beta ma miarę:
Odpowiedzi:
A. 79^{\circ}
B. 82^{\circ}
C. 81^{\circ}
D. 80^{\circ}
E. 78^{\circ}
F. 86^{\circ}
G. 90^{\circ}
H. 84^{\circ}
Zadanie 23. 1 pkt ⋅ Numer: pp-12074 ⋅ Poprawnie: 37/45 [82%]
Rozwiąż
Podpunkt 23.1 (1 pkt)
W każdym
n -kącie wypukłym (
n\geqslant 3 )
liczba przekątnych jest równa
\frac{n(n-3)}{2} .
Wielokątem wypukłym, w którym liczba przekątnych jest o 348
większa od liczby jego boków, jest k -kąt wypukły.
k jest równa:
Odpowiedzi:
A. 35
B. 32
C. 29
D. 33
E. 30
F. 28
Zadanie 24. 1 pkt ⋅ Numer: pp-12075 ⋅ Poprawnie: 37/54 [68%]
Rozwiąż
Podpunkt 24.1 (1 pkt)
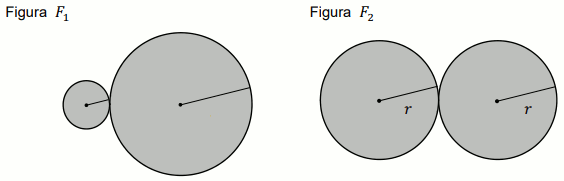
Pole figury
F_1 złożonej z dwóch stycznych zewnętrznie kół
o promieniach
6 i
9 jest równe
polu figury
F_2 złożonej z dwóch stycznych zewnętrznie kół o
promieniach długości
r (zobacz rysunek).
Długość promienia r jest równa:
Odpowiedzi:
A. 2\sqrt{26}
B. \frac{3\sqrt{26}}{2}
C. 3\sqrt{13}
D. \frac{9\sqrt{26}}{2}
E. \frac{3\sqrt{26}}{4}
F. \frac{9\sqrt{26}}{4}
Zadanie 25. 1 pkt ⋅ Numer: pp-12076 ⋅ Poprawnie: 41/58 [70%]
Rozwiąż
Podpunkt 25.1 (1 pkt)
Punkt
A=(3,4) jest wierzchołkiem kwadratu
ABCD , a punkt
M=(0,3) jest punktem
przecięcia się przekątnych tego kwadratu.
Wynika z tego, że pole kwadratu ABCD jest równe:
Odpowiedzi:
A. 17
B. 22
C. 26
D. 19
E. 14
F. 20
Zadanie 26. 1 pkt ⋅ Numer: pp-12077 ⋅ Poprawnie: 54/89 [60%]
Rozwiąż
Podpunkt 26.1 (1 pkt)
Z wierzchołków sześcianu
ABCDEFGH losujemy kolejno dwa
wierzchołki, przy czym drugi wierzchołek losujemy ze zbioru pomniejszonego o wylosowany
za pierwszym razem wierzchołek.
Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu
ABCDEFGH , jest równe:
Odpowiedzi:
A. \frac{4}{7}
B. \frac{3}{7}
C. \frac{2}{7}
D. \frac{1}{7}
E. \frac{1}{14}
F. \frac{3}{14}
Zadanie 27. 1 pkt ⋅ Numer: pp-12078 ⋅ Poprawnie: 132/142 [92%]
Rozwiąż
Podpunkt 27.1 (1 pkt)
Wszystkich liczb naturalnych trzycyfrowych, większych od
600 , w których każda cyfra należy do zbioru
\{1,3,5,6,7,9\} i żadna cyfra się nie powtarza, jest:
Odpowiedzi:
A. 60
B. 66
C. 18
D. 13
E. 79
F. 104
Zadanie 28. 1 pkt ⋅ Numer: pp-12079 ⋅ Poprawnie: 240/227 [105%]
Rozwiąż
Podpunkt 28.1 (1 pkt)
Sześciowyrazowy ciąg liczbowy
(1,2,2x,x+2,5,6) jest niemalejący.
Mediana wyrazów tego ciągu jest równa
\frac{61}{16} .
Wynika z tego, że liczba x jest równa:
Odpowiedzi:
A. \frac{15}{8}
B. \frac{33}{16}
C. \frac{9}{4}
D. \frac{61}{32}
E. \frac{35}{16}
F. \frac{65}{32}
Zadanie 29. 2 pkt ⋅ Numer: pp-21121 ⋅ Poprawnie: 44/45 [97%]
Rozwiąż
Podpunkt 29.1 (1 pkt)
Rozwiąż nierówność
x^2-2x\leqslant 99 .
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych
przedziałów?
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 29.2 (1 pkt)
Podaj największy z końców liczbowych tych przedziałów?
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
Zadanie 30. 2 pkt ⋅ Numer: pp-21122 ⋅ Poprawnie: 50/62 [80%]
Rozwiąż
Podpunkt 30.1 (2 pkt)
Funkcja liniowa
f przyjmuje wartość
-6 dla argumentu
0 , a ponadto
f(12)-f(10)=36 .
Wyznacz wzór funkcji
f(a)=ax+b .
Podaj wartości współczynników a i b .
Odpowiedzi:
Zadanie 31. 2 pkt ⋅ Numer: pp-21123 ⋅ Poprawnie: 33/45 [73%]
Rozwiąż
Podpunkt 31.1 (1 pkt)
Rozwiąż równanie
\frac{3x+17}{3x+13}=-1-x .
Podaj rozwiązanie niecałkowite tego równania.
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 31.2 (1 pkt)
Podaj rozwiązanie całkowite tego równania.
Odpowiedź:
x_{\in\mathbb{Z}}=
(wpisz liczbę całkowitą)
Zadanie 32. 2 pkt ⋅ Numer: pp-21124 ⋅ Poprawnie: 34/93 [36%]
Rozwiąż
Podpunkt 32.1 (2 pkt)
Trójkąt równoboczny
ABC ma pole równe
81\sqrt{3} .
Prosta równoległa do boku
BC przecina boki
AB
i
AC – odpowiednio – w punktach
K i
L . Trójkąty
ABC i
AKL
są podobne, a stosunek długości boków tych trójkątów jest równy
\frac{17}{2} .
Oblicz długość boku trójkąta AKL .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 33. 2 pkt ⋅ Numer: pp-21125 ⋅ Poprawnie: 138/178 [77%]
Rozwiąż
Podpunkt 33.1 (2 pkt)
Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza sumę liczb
wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia
A
polegającego na tym, że suma liczb wyrzuconych oczek jest równa
8 lub
10 lub
11 .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 34. 5 pkt ⋅ Numer: pp-30416 ⋅ Poprawnie: 43/73 [58%]
Rozwiąż
Podpunkt 34.1 (3 pkt)
Punkty
A=(-16,7) i
B=(11,-2)
są wierzchołkami trójkąta równoramiennego
ABC , w którym
|AC|=|BC| . Wierzchołek
C należy do prostej
określonej równaniem
x=4 .
Oblicz współrzędne wierzchołka C=(4, y_C) .
y_C .
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 34.2 (2 pkt)
Oblicz obwód trójkąta
ABC .
Odpowiedź:
L_{\triangle ABC}=
+
\cdot
√
(wpisz trzy liczby całkowite)
Rozwiąż