Podgląd arkusza : lo2@cke-2021-08-pp
Zadanie 1. 1 pkt ⋅ Numer: pp-12107 ⋅ Poprawnie: 291/300 [97%]
Rozwiąż
Podpunkt 1.1 (1 pkt)
Liczba
49^{8}\cdot 7^{-12} jest równa:
Odpowiedzi:
A. 7^{3}
B. 49^{3}
C. 7^{1}
D. 7^{4}
E. 7^{5}
F. 7^{8}
G. 7^{2}
H. 7^{7}
Zadanie 2. 1 pkt ⋅ Numer: pp-12109 ⋅ Poprawnie: 266/265 [100%]
Rozwiąż
Podpunkt 2.1 (1 pkt)
Liczba
\log_{35}{343}+3\log_{35}{5} jest równa:
Odpowiedzi:
A. \log_{35}{5}
B. 4
C. 3
D. \log_{35}{\frac{7}{5}}
E. \log_{35}{\frac{7}{125}}
F. \log_{35}{7}
Zadanie 3. 1 pkt ⋅ Numer: pp-12108 ⋅ Poprawnie: 65/94 [69%]
Rozwiąż
Podpunkt 3.1 (1 pkt)
Liczba
x stanowi
80\%
liczby dodatniej
y . Wynika stąd, że liczba
y
to
p\% liczby
x .
Liczba p zaokrąglona do dwóch miejsc po przecinku jest równa:
Odpowiedzi:
A. 125.00
B. 115.00
C. 135.00
D. 126.00
E. 129.00
F. 127.00
G. 123.00
H. 130.00
Zadanie 4. 1 pkt ⋅ Numer: pp-12110 ⋅ Poprawnie: 224/220 [101%]
Rozwiąż
Podpunkt 4.1 (1 pkt)
Dla każdej liczby rzeczywistej
x i dla każdej liczby rzeczywistej
y wyrażenie
(5x+4y)^2 jest równe:
Odpowiedzi:
A. 25x^2+40xy+16y
B. 5x^2+40xy+4y
C. 25x^2+80xy+16y
D. 25x^2+20xy+16y
E. 25x^2+60xy+16y
F. 25x^2+16y
Zadanie 5. 0.2 pkt ⋅ Numer: pp-12112 ⋅ Poprawnie: 40/46 [86%]
Rozwiąż
Podpunkt 5.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności
5-\frac{2+x}{4}\geqslant 3x+1
jest zbiór:
Odpowiedzi:
A. \left(-\infty, -\frac{28}{13}\right]
B. \left[\frac{14}{13}, +\infty\right)
C. \left[\frac{7}{13}, +\infty\right)
D. \left(-\infty, \frac{7}{13}\right]
E. \left[\frac{28}{13}, +\infty\right)
F. \left(-\infty, \frac{14}{13}\right]
Zadanie 6. 1 pkt ⋅ Numer: pp-12113 ⋅ Poprawnie: 14/22 [63%]
Rozwiąż
Podpunkt 6.1 (1 pkt)
Funkcja liniowa
f jest określona wzorem
f(x)=x+3 . Wykres funkcji
f
przesunięto wzdłuż osi
Ox o
4
jednostki w prawo (tzn. zgodnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji
g .
Funkcja g jest określona wzorem:
Odpowiedzi:
A. g(x)=x+7
B. g(x)=x-3
C. g(x)=-x-1
D. g(x)=x-1
E. g(x)=x+1
F. g(x)=-x-1
Zadanie 7. 1 pkt ⋅ Numer: pp-12114 ⋅ Poprawnie: 44/50 [88%]
Rozwiąż
Podpunkt 7.1 (1 pkt)
Funkcja
f określona jest wxorem
f(x)=ax+1
dla każdej liczby rzeczywistej
x . Miejscem zerowym funkcji
f jest liczba
\frac{11}{4} .
Wtedy a jest równe:
Odpowiedzi:
A. -\frac{8}{33}
B. \frac{8}{11}
C. -\frac{4}{11}
D. -\frac{8}{11}
E. -\frac{2}{11}
F. -\frac{1}{11}
G. \frac{1}{11}
H. \frac{8}{33}
Zadanie 8. 1 pkt ⋅ Numer: pp-12115 ⋅ Poprawnie: 17/29 [58%]
Rozwiąż
Podpunkt 8.1 (1 pkt)
Prosta
k przechodzi przez punkt
A=(1,3) i jest nachylona do osi
Ox pod kątem
45^{\circ} .
Prosta k ma równanie:
Odpowiedzi:
A. y=x+1
B. y=x+3
C. y=x+5
D. y=x+4
E. y=-x+4
F. y=-x
G. y=x
H. y=x+2
Zadanie 9. 1 pkt ⋅ Numer: pp-12116 ⋅ Poprawnie: 103/129 [79%]
Rozwiąż
Podpunkt 9.1 (1 pkt)
Funkcja kwadratowa
f jest określona wzorem
f(x)=-3(x+6)(x-2) . Wierzchołek paraboli,
która jest wykresem funkcji
f , ma współrzędną
x równą:
Odpowiedzi:
A. -3
B. -2
C. -1
D. -7
E. -6
F. 5
G. -4
H. -8
Zadanie 10. 1 pkt ⋅ Numer: pp-12117 ⋅ Poprawnie: 72/102 [70%]
Rozwiąż
Podpunkt 10.1 (1 pkt)
Funkcja
f jest określona wzorem
f(x)=x^2
dla każdej liczby rzeczywistej
x .
Zbiorem wartości funkcji f jest przedział:
Odpowiedzi:
A. (0,+\infty)
B. (-\infty,0]
C. (-\infty,0)
D. [0,+\infty)
Zadanie 11. 1 pkt ⋅ Numer: pp-12118 ⋅ Poprawnie: 15/117 [12%]
Rozwiąż
Podpunkt 11.1 (1 pkt)
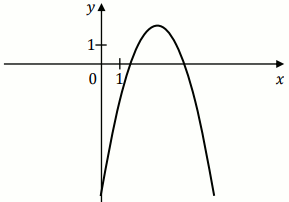
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej
f :
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji f .
Odpowiedzi:
A. y=-5x^2-19x-450
B. y=-5x^2+7x+12
C. y=-5x^2-9x-10
D. y=-5x^2-8x-20
E. y=5x^2+7x+12
F. y=5x^2+7x+12
Zadanie 12. 1 pkt ⋅ Numer: pp-12119 ⋅ Poprawnie: 164/187 [87%]
Rozwiąż
Podpunkt 12.1 (1 pkt)
Ciąg arytmetyczny
(a_n) jest określony dla każdej liczby
naturalnej
n\geqslant 1 . Różnica tego ciągu jest równa
4 .
Wtedy:
Odpowiedzi:
A. a_{16}-a_{7}=40
B. a_{16}-a_{7}=32
C. a_{16}-a_{7}=48
D. a_{16}-a_{7}=36
E. a_{16}-a_{7}=44
F. a_{16}-a_{7}=24
G. a_{16}-a_{7}=52
H. a_{16}-a_{7}=20
Zadanie 13. 1 pkt ⋅ Numer: pp-12120 ⋅ Poprawnie: 81/147 [55%]
Rozwiąż
Podpunkt 13.1 (1 pkt)
Suma wszystkich liczb całkowitych dodatnich parzystych i jednocześnie mniejszych od
701 jest równa:
Odpowiedzi:
A. \frac{2+350}{2}\cdot 701
B. \frac{2+1402}{2}\cdot 350
C. \frac{2+1402}{2}\cdot 701
D. \frac{2+700}{2}\cdot 701
E. \frac{2+701}{2}\cdot 350
F. \frac{2+700}{2}\cdot 350
G. \frac{2+350}{2}\cdot 350
H. \frac{2+701}{2}\cdot 701
Zadanie 14. 1 pkt ⋅ Numer: pp-12121 ⋅ Poprawnie: 90/93 [96%]
Rozwiąż
Podpunkt 14.1 (1 pkt)
Trójwyrazowy ciąg
(4,x,144) jest rosnącym ciągiem
geometrycznym.
Wtedy x jest równe:
Odpowiedzi:
A. 24
B. 21
C. 27
D. 22
E. 23
F. 20
Zadanie 15. 1 pkt ⋅ Numer: pp-12122 ⋅ Poprawnie: 20/22 [90%]
Rozwiąż
Podpunkt 15.1 (1 pkt)
Kąt
\alpha jest ostry i
\sin\alpha=\frac{5}{13} .
Wynika stąd, że \cos\alpha jest równy:
Odpowiedzi:
A. \frac{144}{169}
B. \frac{\sqrt{3}}{676}
C. \frac{64}{169}
D. \frac{\sqrt{3}}{13}
E. \frac{8}{13}
F. \frac{12}{13}
Zadanie 16. 1 pkt ⋅ Numer: pp-12123 ⋅ Poprawnie: 20/22 [90%]
Rozwiąż
Podpunkt 16.1 (1 pkt)
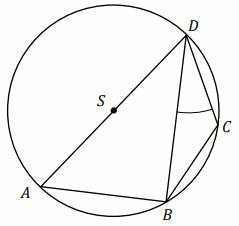
Czworokąt
ABCD jest wpisany w okrąg o środku
S . Bok
AD jest średnicą tego okręgu,
a miara kąta
BDC jest równa
37^{\circ} (zobacz rysunek).
Wtedy miara stopniowa kąta BSC jest równa:
Odpowiedzi:
A. 79^{\circ}
B. 74^{\circ}
C. 71^{\circ}
D. 72^{\circ}
E. 76^{\circ}
F. 73^{\circ}
G. 78^{\circ}
H. 68^{\circ}
Zadanie 17. 1 pkt ⋅ Numer: pp-12124 ⋅ Poprawnie: 15/22 [68%]
Rozwiąż
Podpunkt 17.1 (1 pkt)
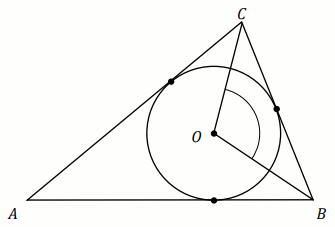
Okrąg o środku w punkcie
O jest wpisany w trójkąt
ABC . Wiadomo, że
|AB|=|AC| i
|\sphericalangle BOC|=122^{\circ} (zobacz rysunek).
Miara stopniowa kąta BAC jest równa:
Odpowiedzi:
A. 68
B. 60
C. 66
D. 70
E. 67
F. 64
Zadanie 18. 1 pkt ⋅ Numer: pp-12125 ⋅ Poprawnie: 15/22 [68%]
Rozwiąż
Podpunkt 18.1 (1 pkt)
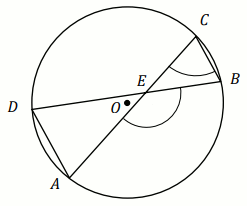
Punkty
A ,
B ,
C i
D leżą na okręgu o środku w punkcie
O .
Cięciwy
DB i
AC przecinają się
w punkcie
E ,
|\sphericalangle ACB|=57^{\circ} oraz
|\sphericalangle AEB|=136^{\circ} (zobacz rysunek).
Miara stopniowa kąta DAC jest równa:
Odpowiedzi:
A. 83^{\circ}
B. 85^{\circ}
C. 76^{\circ}
D. 84^{\circ}
E. 79^{\circ}
F. 75^{\circ}
G. 81^{\circ}
H. 77^{\circ}
Zadanie 19. 1 pkt ⋅ Numer: pp-12126 ⋅ Poprawnie: 31/40 [77%]
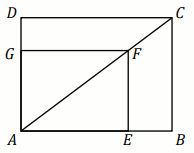
Rozwiąż
Podpunkt 19.1 (1 pkt)
Przekątna
AC prostokąta
ABCD ma
długość
82 . Na boku
AB obrano
punkt
E , na przekątnej
AC obrano punkt
F , a na boku
AD obrano punkt
G – tak, że czworokąt
AEFG jest
prostokątem (zobacz rysunek). Ponadto
|EF|=9 i
|GF|=40 .
Obwód prostokąta ABCD jest równy:
Odpowiedzi:
A. 294
B. \frac{392}{3}
C. \frac{784}{5}
D. 196
E. 49
F. 147
Zadanie 20. 1 pkt ⋅ Numer: pp-12127 ⋅ Poprawnie: 35/39 [89%]
Rozwiąż
Podpunkt 20.1 (1 pkt)
W układzie współrzędnych dane są dwa punkty
A=(4,-6)
i
B=(-6,6) .
Współczynnik kierunkowy prostej AB jest równy:
Odpowiedzi:
A. -\frac{3}{5}
B. \frac{4}{5}
C. -\frac{3}{10}
D. -\frac{12}{5}
E. \frac{12}{5}
F. \frac{9}{5}
G. -\frac{9}{5}
H. -\frac{6}{5}
Zadanie 21. 1 pkt ⋅ Numer: pp-12128 ⋅ Poprawnie: 34/36 [94%]
Rozwiąż
Podpunkt 21.1 (1 pkt)
Prosta
k ma równanie
y=\frac{2}{9}x+10 .
Współczynnik kierunkowy prostej prostopadłej do prostej k jest równy:
Odpowiedzi:
A. -3
B. -\frac{3}{2}
C. \frac{9}{4}
D. -\frac{27}{4}
E. \frac{27}{4}
F. -9
G. -\frac{9}{4}
H. -\frac{9}{2}
Zadanie 22. 1 pkt ⋅ Numer: pp-12129 ⋅ Poprawnie: 28/35 [80%]
Rozwiąż
Podpunkt 22.1 (1 pkt)
Punkty
A=(3,1) i
C=(2,4) są końcami przekątnej kwadratu
ABCD .
Promień okręgu opisanego na tym kwadracie jest równy:
Odpowiedzi:
A. \frac{\sqrt{5}}{2}
B. \frac{\sqrt{10}}{2}
C. \sqrt{10}
D. \frac{\sqrt{10}}{8}
E. \frac{3\sqrt{10}}{4}
F. \frac{\sqrt{10}}{4}
G. \sqrt{5}
H. \frac{\sqrt{5}}{2}
Zadanie 23. 1 pkt ⋅ Numer: pp-12130 ⋅ Poprawnie: 26/39 [66%]
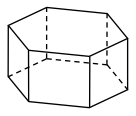
Rozwiąż
Podpunkt 23.1 (1 pkt)
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość
równą
6\sqrt{5} (zobacz rysunek).
Pole powierzchni całkowitej tego graniastosłupa jest równe:
Odpowiedzi:
A. 540+540\sqrt{3}
B. 1080+540\sqrt{3}
C. 1080+540\sqrt{6}
D. 1080+360\sqrt{3}
E. 1080+1080\sqrt{3}
F. 720+1080\sqrt{3}
G. 1080+540\sqrt{2}
H. 720+540\sqrt{3}
Zadanie 24. 1 pkt ⋅ Numer: pp-12131 ⋅ Poprawnie: 15/23 [65%]
Rozwiąż
Podpunkt 24.1 (1 pkt)
Przekątna sześcianu jest równa
12\sqrt{5} .
Wynika stąd, że objętość tego sześcianu jest równa:
Odpowiedzi:
A. 1920\sqrt{15}
B. 2880\sqrt{15}
C. 960\sqrt{5}
D. 960\sqrt{15}
E. 2880\sqrt{5}
F. 960\sqrt{10}
G. 1440\sqrt{15}
H. 2880\sqrt{15}
Zadanie 25. 1 pkt ⋅ Numer: pp-12132 ⋅ Poprawnie: 99/115 [86%]
Rozwiąż
Podpunkt 25.1 (1 pkt)
Wszystkich liczb naturalnych pięciocyfrowych parzystych jest:
Odpowiedzi:
A. 9\cdot 5\cdot 10^3
B. 9\cdot 2\cdot 10^3
C. 4\cdot 10^5
D. 5\cdot 10^4
Zadanie 26. 1 pkt ⋅ Numer: pp-12133 ⋅ Poprawnie: 81/92 [88%]
Rozwiąż
Podpunkt 26.1 (1 pkt)
W pudełku znajdują się tylko kule białe i kule czerwone. Stosunek liczby kul białych
do liczby kul czerwonych jest równy
6:9 . Wylosowanie
każdej kuli z tego pudełka jest jednakowo prawdopodobne. Losujemy jedną kulę. Niech
A oznacza zdarzenie polegające na tym, że wylosowana z pudełka
kula będzie czerwona.
Prawdopodobieństwo zdarzenia A jest równe:
Odpowiedzi:
A. \frac{4}{5}
B. \frac{2}{5}
C. \frac{4}{15}
D. \frac{3}{5}
E. \frac{3}{10}
F. \frac{12}{25}
Zadanie 27. 1 pkt ⋅ Numer: pp-12134 ⋅ Poprawnie: 155/137 [113%]
Rozwiąż
Podpunkt 27.1 (1 pkt)
Średnia arytmetyczna pięciu liczb:
5x+6 ,
6x+7 ,
7x+8 ,
8x+9 ,
9x+10 , jest równa
43 .
Wtedy x jest równe:
Odpowiedzi:
A. 5
B. 9
C. \frac{21}{4}
D. 4
E. 6
F. \frac{11}{2}
G. 8
H. 3
Zadanie 28. 2 pkt ⋅ Numer: pp-21132 ⋅ Poprawnie: 17/22 [77%]
Rozwiąż
Podpunkt 28.1 (1 pkt)
Rozwiąż nierówność:
x^2+6\geqslant 7x .
Rozwiązanie tej nierówności zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców
liczbowych tych przedziałów.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 28.2 (1 pkt)
Podaj największy z końców liczbowych tych przedziałów.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
Zadanie 29. 2 pkt ⋅ Numer: pp-21133 ⋅ Poprawnie: 11/22 [50%]
Rozwiąż
Podpunkt 29.1 (1 pkt)
Rozwiąż równanie:
\frac{x+14}{x-1}=2x+12 .
Podaj rozwiązanie niecałkowite tego równania.
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 29.2 (1 pkt)
Podaj rozwiązanie całkowite tego równania.
Odpowiedź:
x_{\in \mathbb{Z}}=
(wpisz liczbę całkowitą)
Zadanie 30. 2 pkt ⋅ Numer: pp-21134 ⋅ Poprawnie: 33/71 [46%]
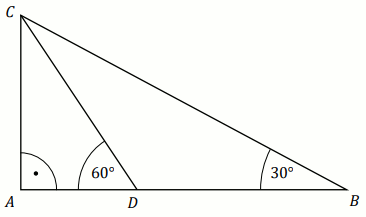
Rozwiąż
Podpunkt 30.1 (2 pkt)
W trójkącie
ABC kąt przy wierzchołku
A jest prosty,
a kąt przy wierzchołku
B ma miarę
30^{\circ} .
Na boku
AB tego trójkąta obrano punkt
D tak,
że miara kąta
CDA jest równa
60^{\circ} oraz
|AD|=26 (zobacz rysunek).
Oblicz |BD| .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 31. 2 pkt ⋅ Numer: pp-21135 ⋅ Poprawnie: 36/110 [32%]
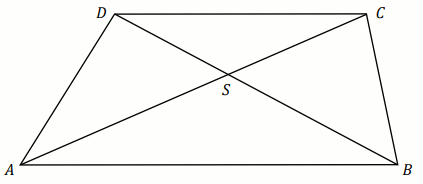
Rozwiąż
Podpunkt 31.1 (2 pkt)
Dany jest trapez
ABCD o podstawach
AB i
CD . Przekątne
AC i
BD
tego trapezu przecinają się w punkcie
S (zobacz rysunek) tak, że
|AS|:|SC|=7:2 .
Pole trójkąta ABS jest równe 38 . Oblicz pole trójkąta
CDS .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 32. 2 pkt ⋅ Numer: pp-21136 ⋅ Poprawnie: 71/113 [62%]
Rozwiąż
Podpunkt 32.1 (2 pkt)
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry,
która na każdej ściance ma inną liczbę oczek – od jednego do sześciu oczek. Niech
A oznacza zdarzenie polegające na tym, że iloczyn liczb oczek
wyrzuconych w dwóch rzutach jest równy
12 .
Oblicz prawdopodobieństwo zdarzenia A .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 33. 5 pkt ⋅ Numer: pp-30418 ⋅ Poprawnie: 11/38 [28%]
Rozwiąż
Podpunkt 33.1 (3 pkt)
Dany jest ciąg
(a_n) określony wzorem
a_n=\frac{15}{2}n-51 dla każdej liczby naturalnej
n\geqslant 1 . Trójwyrazowy ciąg
(a_{10}, x^2+2, a_{14}) , gdzie
x
jest liczbą rzeczywistą dodatnią, jest geometryczny i rosnący.
Oblicz x .
Odpowiedź:
x=
\cdot √
(wpisz dwie liczby całkowite)
Podpunkt 33.2 (2 pkt)
Oblicz iloraz tego ciągu.
Odpowiedź:
Rozwiąż