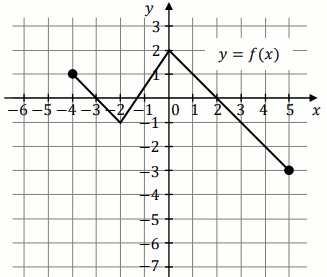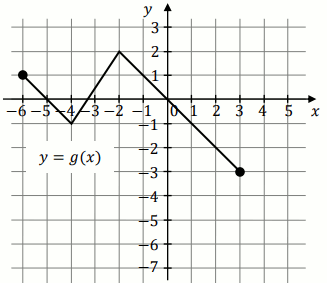⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd arkusza : lo2@cke-2022-05-pp
| Zadanie 1. 1 pkt ⋅ Numer: pp-11849 ⋅ Poprawnie: 299/356 [83%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Liczba (3\sqrt{32}-2\sqrt{2})^2 jest równa:
Odpowiedzi:
| A. 208 | B. 204 |
| C. 201 | D. 200 |
| E. 205 | F. 196 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11850 ⋅ Poprawnie: 280/376 [74%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Dodatnie liczby x i y spełniają warunek
3x=2y. Wynika stąd, że wartość wyrażenia
\frac{x^2+y^2}{x\cdot y} jest równa:
Odpowiedzi:
| A. \frac{13}{6} | B. \frac{13}{4} |
| C. \frac{13}{24} | D. \frac{13}{3} |
| E. \frac{13}{9} | F. \frac{13}{12} |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11851 ⋅ Poprawnie: 535/594 [90%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Liczba 7\log_{4}{2}+2\log_{4}{8} jest równa:
Odpowiedzi:
| A. \frac{37}{4} | B. \frac{13}{4} |
| C. \frac{13}{3} | D. \frac{13}{2} |
| E. 13 | F. \frac{26}{3} |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11852 ⋅ Poprawnie: 310/396 [78%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Cena działki po kolejnych dwóch obniżkach, za każdym razem o 10\%
w odniesieniu do ceny obowiązującej w danym momencie, jest równa 70227.00 zł.
Cena w złotych tej działki przed obiema obniżkami była, w zaokrągleniu do 1 zł, równa:
Odpowiedzi:
| A. 86799 | B. 86798 |
| C. 86700 | D. 86763 |
| E. 86790 | F. 86796 |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11853 ⋅ Poprawnie: 387/616 [62%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Liczba 3^{4+\frac{1}{4}} jest równa liczbie
\sqrt[m]{3^n}.
Podaj liczby m i n.
Odpowiedzi:
| m | = |
(wpisz liczbę całkowitą) |
| n | = |
(wpisz liczbę całkowitą) |
| Zadanie 6. 1 pkt ⋅ Numer: pp-11854 ⋅ Poprawnie: 320/418 [76%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Rozwiązaniem układu równań
\begin{cases}
x+6y=-26\\
4x-5y=12
\end{cases}
jest para liczb: x=x_0, y=y_0.
Wtedy:
Odpowiedzi:
| A. x_0>0\ \wedge\ y>0 | B. x_0\lessdot\ \wedge\ y\lessdot 0 |
| C. x_0>0\ \wedge\ y\lessdot 0 | D. x_0\lessdot 0\ \wedge\ y> 0 |
| Zadanie 7. 1 pkt ⋅ Numer: pp-11855 ⋅ Poprawnie: 229/320 [71%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Zbiorem wszystkich rozwiązań nierówności 1-\frac{x}{2}>\frac{x}{3},
jest przedział:
Odpowiedzi:
| A. \left(\frac{12}{5},+\infty\right) | B. \left(-\infty,\frac{6}{5}\right) |
| C. \left(-\infty,\frac{3}{5}\right) | D. \left(-\infty,-\frac{6}{5}\right) |
| E. \left(-\frac{6}{5},+\infty\right) | F. \left(-\infty,-\frac{12}{5}\right) |
| Zadanie 8. 1 pkt ⋅ Numer: pp-11856 ⋅ Poprawnie: 195/222 [87%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Suma wszystkich rozwiązań równania 5x(x^2-9)(x-6)=0 jest równa:
Odpowiedzi:
| A. 7 | B. -1 |
| C. 3 | D. -2 |
| E. 1 | F. 6 |
| Zadanie 9. 1 pkt ⋅ Numer: pp-11857 ⋅ Poprawnie: 366/478 [76%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
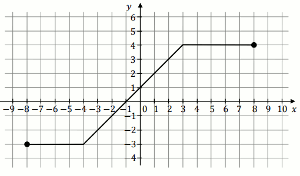
Na rysunku przedstawiono wykres funkcji f:
Iloczyn f(-2)\cdot f(-5)\cdot f(-7) jest równy:
Odpowiedzi:
| A. -13 | B. -9 |
| C. -1 | D. -6 |
| E. -3 | F. -12 |
| Zadanie 10. 1 pkt ⋅ Numer: pp-11858 ⋅ Poprawnie: 257/432 [59%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Na rysunku 1. przedstawiono wykres funkcji f określonej na zbiorze
[-4,5]:
Funkcję g określono za pomocą funkcji f.
Wykres funkcji g przedstawiono na rysunku 2:
Wynika stąd, że:
Odpowiedzi:
| A. g(x)=f(-x)-2 | B. g(x)=f(x-2) |
| C. g(x)=f(x)+2 | D. g(x)=f(x+2) |
| E. g(x)=f(-x)+2 | F. g(x)=f(x)-2 |
| Zadanie 11. 1 pkt ⋅ Numer: pp-11859 ⋅ Poprawnie: 254/357 [71%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Miejscem zerowym funkcji liniowej f określonej wzorem
f(x)=-\frac{1}{4}(x-3)-5 jest liczba:
Odpowiedzi:
| A. -\frac{17}{3} | B. -\frac{17}{2} |
| C. -\frac{34}{3} | D. -34 |
| E. -\frac{51}{2} | F. -17 |
| Zadanie 12. 1 pkt ⋅ Numer: pp-11864 ⋅ Poprawnie: 338/461 [73%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Wykresem funkcji kwadratowej f(x)=3x^2+bx+c jest parabola o wierzchołku
w punkcie W=(-2,-4). Wzór tej funkcji w postaci kanonicznej to:
Odpowiedzi:
| A. f(x)=3(x+2)^2-4 | B. f(x)=3(x+4)^2-2 |
| C. f(x)=3(x-2)^2+4 | D. f(x)=3(x-2)^2-4 |
| E. f(x)=3(x+2)^2+4 | F. f(x)=3(x-4)^2-2 |
| Zadanie 13. 1 pkt ⋅ Numer: pp-11860 ⋅ Poprawnie: 272/284 [95%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
Ciąg \left(a_n\right) jest określony wzorem
a_n=\frac{3n^2-12n}{n} dla każdej liczby
naturalnej n\geqslant 1.
Wtedy wyraz a_7 jest równy:
Odpowiedzi:
| A. 21 | B. 24 |
| C. 3 | D. 18 |
| E. 9 | F. 6 |
| Zadanie 14. 1 pkt ⋅ Numer: pp-11861 ⋅ Poprawnie: 494/501 [98%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
W ciągu arytmetycznym (a_n), określonym dla każdej liczby naturalnej
n\geqslant 1, a_5=-26 oraz
a_{10}=-51. Różnica tego ciągu jest równa:
Odpowiedzi:
| A. -\frac{5}{2} | B. -5 |
| C. 1 | D. -7 |
| E. -2 | F. -\frac{7}{2} |
| Zadanie 15. 1 pkt ⋅ Numer: pp-11862 ⋅ Poprawnie: 233/308 [75%] | Rozwiąż |
Podpunkt 15.1 (1 pkt)
Wszystkie wyrazy nieskończonego ciągu geometrycznego \left(a_n\right), określonego dla każdej
liczby naturalnej n\geqslant 1, są dodatnie i
9a_5=16a_3.
Wtedy iloraz tego ciągu jest równy:
Odpowiedzi:
| A. \frac{8}{3} | B. \frac{4}{3} |
| C. \frac{8}{9} | D. 2 |
| E. \frac{16}{9} | F. 1 |
| Zadanie 16. 1 pkt ⋅ Numer: pp-11863 ⋅ Poprawnie: 197/237 [83%] | Rozwiąż |
Podpunkt 16.1 (1 pkt)
Liczba \cos 21^{\circ}\cdot\sin 69^{\circ}+\sin 21^{\circ}\cdot\cos 69^{\circ}
jest równa:
Odpowiedzi:
| A. \frac{\sqrt{3}}{2} | B. \frac{1}{2} |
| C. \frac{\sqrt{2}}{2} | D. 1 |
| Zadanie 17. 1 pkt ⋅ Numer: pp-11866 ⋅ Poprawnie: 133/221 [60%] | Rozwiąż |
Podpunkt 17.1 (1 pkt)
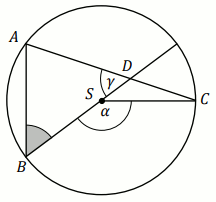
Punkty A, B, C
leżą na okręgu o środku S. Punkt D jest punktem
przecięcia cięciwy AC i średnicy okręgu poprowadzonej z punktu
B. Miara kąta BSC jest równa
110^{\circ}, a miara kąta ADBjest równa
\gamma (zobacz rysunek).
Wtedy kąt ABD ma miarę:
Odpowiedzi:
| A. 153^{\circ}-\gamma | B. 125^{\circ}-\gamma |
| C. 92^{\circ}-\gamma | D. 107^{\circ}-\gamma |
| E. 144^{\circ}-\frac{\gamma}{2} | F. 125^{\circ}-2\gamma |
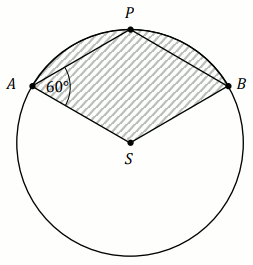
| Zadanie 18. 1 pkt ⋅ Numer: pp-11874 ⋅ Poprawnie: 169/249 [67%] | Rozwiąż |
Podpunkt 18.1 (1 pkt)
Punkty A, B, P leżą
na okręgu o środku S i promieniu długości 6.
Czworokąt ASBP jest rombem, w którym kąt ostry PAS
ma miarę 60^{\circ} (zobacz rysunek).
Pole powierzchni zakreskowanej na rysunku figury jest równe:
Odpowiedzi:
| A. 36\pi | B. 12\pi |
| C. 6\pi | D. 9\pi |
| E. 3\pi | F. 24\pi |
| Zadanie 19. 1 pkt ⋅ Numer: pp-11848 ⋅ Poprawnie: 233/392 [59%] | Rozwiąż |
Podpunkt 19.1 (1 pkt)
Wysokość trójkąta równobocznego jest równa 4\sqrt{3}. Pole powierzchni
tego trójkąta jest równe:
Odpowiedzi:
| A. 4\sqrt{3} | B. 24\sqrt{3} |
| C. 8\sqrt{3} | D. 16 |
| E. 16\sqrt{3} | F. 48 |
| Zadanie 20. 1 pkt ⋅ Numer: pp-11871 ⋅ Poprawnie: 196/261 [75%] | Rozwiąż |
Podpunkt 20.1 (1 pkt)
Boki równoległoboku mają długości 3 i 2,
a kąt rozwarty między tymi bokami ma miarę 120^{\circ}. Pole powierzchni
tego równoległoboku jest równe:
Odpowiedzi:
| A. \frac{12\sqrt{3}}{5} | B. 6\sqrt{3} |
| C. \frac{9\sqrt{3}}{2} | D. 3\sqrt{3} |
| E. \frac{3\sqrt{3}}{2} | F. \sqrt{3} |
| Zadanie 21. 1 pkt ⋅ Numer: pp-11865 ⋅ Poprawnie: 237/360 [65%] | Rozwiąż |
Podpunkt 21.1 (1 pkt)
Punkty A=(6,-5) oraz B=(30,b) leżą
na prostej, która przechodzi przez początek układu współrzędnych.
Wtedy b jest równe:
Odpowiedzi:
| A. -\frac{125}{6} | B. -25 |
| C. -50 | D. -\frac{25}{3} |
| E. -\frac{25}{2} | F. -\frac{100}{3} |
| Zadanie 22. 1 pkt ⋅ Numer: pp-11870 ⋅ Poprawnie: 229/341 [67%] | Rozwiąż |
Podpunkt 22.1 (1 pkt)
Dane są cztery proste k, l,
m, n o równaniach:
k:y=\frac{2}{5}x+2, l:y=-\frac{4}{5}x-3
m:y=\frac{4}{5}x+4, n:y=-\frac{5}{4}x-6
Wśród tych prostych prostopadłe są proste:
Odpowiedzi:
| A. k i l | B. m i n |
| C. k i m | D. k i n |
| Zadanie 23. 1 pkt ⋅ Numer: pp-11867 ⋅ Poprawnie: 216/265 [81%] | Rozwiąż |
Podpunkt 23.1 (1 pkt)
Punkty K=(-4,-5) i L=(b,0)
są końcami odcinka KL. Pierwsza współrzędna środka odcinka
KL jest równa 11.
Wynika stąd, że:
Odpowiedzi:
| A. b=\frac{26}{3} | B. b=\frac{65}{2} |
| C. b=\frac{104}{3} | D. b=\frac{52}{3} |
| E. b=26 | F. b=13 |
| Zadanie 24. 1 pkt ⋅ Numer: pp-11869 ⋅ Poprawnie: 151/238 [63%] | Rozwiąż |
Podpunkt 24.1 (1 pkt)
Punkty A=(-4,3) i B=(2,5)
są sąsiednimi wierzchołkami kwadratu ABCD.
Przekątna tego kwadratu ma długość:
Odpowiedzi:
| A. 2\sqrt{10} | B. 4\sqrt{5} |
| C. \sqrt{5} | D. 8\sqrt{5} |
| E. 2\sqrt{5} | F. 4\sqrt{10} |
| Zadanie 25. 1 pkt ⋅ Numer: pp-11875 ⋅ Poprawnie: 184/243 [75%] | Rozwiąż |
Podpunkt 25.1 (1 pkt)
Podstawą graniastosłupa prostego jest romb o przekątnych długości 15
cm i 5 cm. Wysokość tego graniastosłupa jest krótsza od dłuższej
przekątnej rombu o 7 cm.
Wtedy objętość tego graniastosłupa jest równa:
Odpowiedzi:
| A. 150 | B. 450 |
| C. 200 | D. 180 |
| E. 225 | F. 300 |
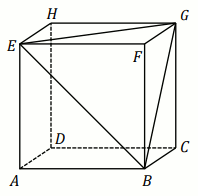
| Zadanie 26. 1 pkt ⋅ Numer: pp-11876 ⋅ Poprawnie: 205/344 [59%] | Rozwiąż |
Podpunkt 26.1 (1 pkt)
Dany jest sześcian ABCDEFGH o krawędzi długości 2.
Punkty E, F, G,
B są wierzchołkami ostrosłupa EFGB
(zobacz rysunek).
Pole powierzchni całkowitej ostrosłupa EFGB jest równe:
Odpowiedzi:
| A. \frac{24+8\sqrt{3}}{3} | B. 6+2\sqrt{3} |
| C. 9+3\sqrt{3} | D. \frac{3+\sqrt{3}}{2} |
| E. 3+\sqrt{3} | F. 12+4\sqrt{3} |
| Zadanie 27. 1 pkt ⋅ Numer: pp-11873 ⋅ Poprawnie: 443/577 [76%] | Rozwiąż |
Podpunkt 27.1 (1 pkt)
Wszystkich różnych liczb naturalnych czterocyfrowych nieparzystych podzielnych przez
5 jest:
Odpowiedzi:
| A. 9\cdot 8\cdot 7\cdot 1 | B. 9\cdot 9\cdot 9\cdot 1 |
| C. 9\cdot 9\cdot 8\cdot 1 | D. 9\cdot 10\cdot 10\cdot 1 |
| Zadanie 28. 1 pkt ⋅ Numer: pp-11877 ⋅ Poprawnie: 227/293 [77%] | Rozwiąż |
Podpunkt 28.1 (1 pkt)
Średnia arytmetyczna zestawu sześciu liczb: 2x-5,4,6,8,11,13 jest równa
\frac{13}{2}.
Wynika stąd, że
Odpowiedzi:
| A. x=-3 | B. x=-2 |
| C. x=-1 | D. x=1 |
| E. x=2 | F. x=0 |
| Zadanie 29. 2 pkt ⋅ Numer: pp-21068 ⋅ Poprawnie: 179/314 [57%] | Rozwiąż |
Podpunkt 29.1 (1 pkt)
Rozwiąż nierówność
2x^2+7x+8 > 5.
Rozwiązanie zapisz w postaci przedziału lub sumy przedziałów. Podaj ten z końców liczbowych, który jest liczba całkowitą.
Odpowiedź:
x_{\in\mathbb{Z}}=
(wpisz liczbę całkowitą)
Podpunkt 29.2 (1 pkt)
Podaj ten z końców liczbowych, który nie jest liczbą całkowitą.
Odpowiedź:
| x_{\notin\mathbb{Z}}= | |
| Zadanie 30. 2 pkt ⋅ Numer: pp-21069 ⋅ Poprawnie: 202/344 [58%] | Rozwiąż |
Podpunkt 30.1 (2 pkt)
W ciągu arytmetycznym \left(a_n\right), określonym dla każdej liczby
naturalnej n\geqslant 1, a_1=-2 i
a_4=-11.
Oblicz sumę stu początkowych kolejnych wyrazów tego ciągu.
Odpowiedź:
S_{100}=
(wpisz liczbę całkowitą)
| Zadanie 31. 2 pkt ⋅ Numer: pp-21070 ⋅ Poprawnie: 122/224 [54%] | Rozwiąż |
Podpunkt 31.1 (2 pkt)
Kąt \alpha jest ostry i \tan\alpha=5.
Oblicz wartość wyrażenia \sin^2\alpha.
Odpowiedź:
| \sin^2\alpha= | |
| Zadanie 32. 2 pkt ⋅ Numer: pp-21071 ⋅ Poprawnie: 214/368 [58%] | Rozwiąż |
Podpunkt 32.1 (2 pkt)
Ze zbioru dziewięcioelementowego M=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}
losujemy kolejno bez zwracania dwa razy po jednej liczbie. Zdarzenie A
polega na wylosowaniu dwóch liczb ze zbioru M, których iloczyn jest równy
18.
Oblicz prawdopodobieństwo zajścia zdarzenia A.
Odpowiedź:
| P(A)= | |
| Zadanie 33. 5 pkt ⋅ Numer: pp-30407 ⋅ Poprawnie: 87/345 [25%] | Rozwiąż |
Podpunkt 33.1 (2 pkt)
Wykres funkcji kwadratowej f określonej wzorem
f(x)=ax^2+bx+c ma z prostą o równaniu
y=1 dokładnie jeden punkt wspólny.
Punkty A=(8,0) i B=(6,0)
należą do wykresu funkcji f.
Wyznacz współrzędne wierzchołka paraboli będącego wykresem funkcji f.
Odpowiedzi:
| x_w | = |
(wpisz liczbę całkowitą) |
| y_w | = |
(wpisz liczbę całkowitą) |
Podpunkt 33.2 (3 pkt)
Wyznacz współczynniki a, b i c.
Odpowiedzi:
| a | = | (dwie liczby całkowite) | |
| b | = | (dwie liczby całkowite) | |
| c | = | (dwie liczby całkowite) | |