Podgląd arkusza : lo2@cke-2023-05-pp

 Zbiór A=(-\infty, -5\rangle\cup\langle 4,+\infty) jest rozwiązaniem nierówności:

 Liczba \sqrt[3]{-\frac{343}{432}}\cdot\sqrt[3]{2} jest równa:

 Liczba \log_{9}{27}+\log_{9}{3} jest równa:

 Dla każdej liczby rzeczywistej a wyrażenie (3a-5)^2-(3a+5)^2 jest równe:

 Zbiorem wszystkich rozwiązań nierówności -2(x-2)\leqslant\frac{7-x}{3} jest przedział:

 Jednym z rozwiązań równania \sqrt{7}\cdot (x^2-8)(x+3)=0 jest liczba:

 Równanie \frac{(x+3)(x+7)^2}{(x-7)(x+3)^2}=0:

 Rozwiąż równanie 3x^3-7x^2-12x+28=0.

Podaj najmniejsze rozwiązanie tego równania.

 Podaj największe rozwiązanie tego równania.

 Punkt A=(2,-3) należy do obu prostych k i l. Prosta k przecina oś Oy w punkcie o rzędnej 3, zas prosta l przecina oś Oy w punkcie o rzędnej -1.

Wskaż układ równań, którego interpretację opisano powyżej:

 Dany jest prostokąt o bokach długości a i b, gdzie a>b. Obwód tego prostokąta jest równy 46. Jeden z boków tego prostokąta jest o 5 krótszy od drugiego. Oceń, które z podanych układów równań opisują zależności pomiędzy bokami tego prostokąta.

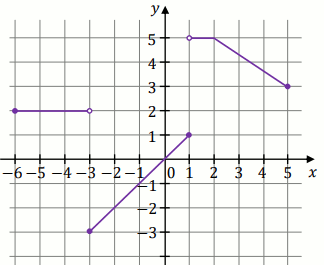
 Na rysunku przedstawiono wykres funkcji określonej wzorem y=f(x):

Dziedziną tej funkcji jest zbiór:

 Największa wartość tej funkcji w przedziale [-5,1] jest równa:

 Funkcja f jest malejąca w zbiorze:

 Wykres funkcji liniowej określonej wzorem f(x)=ax+b, przechodzi przez pierwszą, drugą i czwartą ćwiartkę układu współrzędnych.

Wówczas liczby a i b spełniają warunki:

 Jednym z miejsc zerowych funkcji kwadratowej f jest liczba 5. Pierwsza współrzędna wierzchołka paraboli, będącej wykresem tej funkcji jest równa 0.

Drugim miejscem zerowym funkcji f jest liczba:

 Ciąg \left(a_n\right) jest określony wzorem a_n=2^n\cdot(n+2), dla każdej dodatniej liczby naturalnej n.

Wyraz a_6 jest równy:

 Ciąg liczbowy (27, 9, a-6) jest ciągiem geometrycznym.

Liczba a jest równa:

 Pan Stanisław spłacił pożyczkę w wysokości 13680 zł w osiemnastu ratach. Każda kolejna rata była mniejsza od poprzedniej o 40 zł.

Oblicz kwotę pierwszej raty.

 Wierzchołek kąta znajduje się w punkcie O=(0,0), a do jego ramion należą punkty A=(-4,3) oraz B=(2,0).

Tangens kąta AOB jest równy:

 Dla każdego kąta ostrego \alpha wyrażenie 3\sin^4\alpha+3\sin^2\alpha\cdot\cos^2\alpha jest równe:

 W rombie o boku długości 4\sqrt{7} kąt rozwarty ma miarę 150^{\circ}.

Iloczyn długości przekątnych tego rombu jest równy:

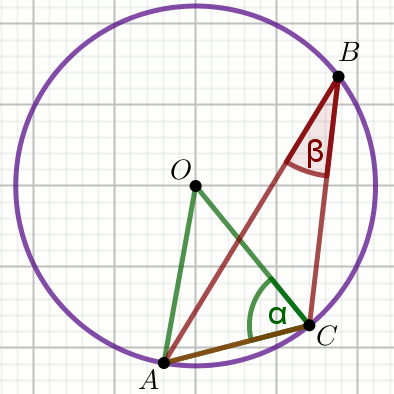
 Punkty A, B i C należą do okręgu o środku w punkcie O, a kąt \alpha ma miarę 68^{\circ}:

Miara kąta \beta jest równa:

 Trójkaty T_1 i T_2 są podobne. Przyprostokatne trójkąta T_1 mają długość 5 i 12. Przeciwprostokątna trójkąta T_2 ma długość 52.

Oblicz pole powierzchni trójkąta T_2.

 Dane są proste o równaniach: k:y=\frac{2}{3}x oraz l:y=-\frac{3}{2}x-39.

Oceń prawdziwość podanych odpowiedzi:

 Oceń prawdziwość podanych odpowiedzi:

 Prosta k określona jest równaniem k:y=-\frac{1}{3}x-1. Prosta l:y=ax+b jest równoległa do prostej k i należy do niej punkt P=(-9,6).

Wówczas:

 Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 2\sqrt{14}. Przekątna tego graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem \alpha takim, że \cos\alpha=\frac{2\sqrt{7}}{5}.

Długość przekątnej tego graniastosłupa jest równa:

 Wysokość ściany bocznej ostrosłupa prawidłowego czworokątnego ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 30^{\circ}.

Oblicz objętość tego ostrosłupa.

 Oblicz pole powierzchni tego ostrosłupa.

 W pewnym ostrosłupie prawidłowym stosunek liczby W wszystkich wierzchołków do liczby K wszystkich krawędzi jest równy \frac{7}{12}.

Podstawą tego ostrosłupa jest n-kąt foremny. Liczba n jest równa:

 Wszystkich liczb naturalnych 6-ciocyfrowych, w których zapisie dziesiętnym występują tylko cyfry 0, 5 i 7 (np. 57\ 075), jest:

 Na diagramie poniżej przedstawiono ceny pomidorów w n=17 wybranych sklepach.

Ilość sklepów :      3 |    4 |    3 |    3 |    4 |
Cena pomidorów:   5.50 | 5.80 | 5.90 | 6.00 | 6.30 |

Podaj medianę ceny pomidorów w tych wybranych sklepach.

 Podaj średnią cenę kilograma pomidorów w tych wybranych sklepach.

 Ze zbioru ośmiu liczb \{2, 3, 4, 5, 6, 7, 8, 9\} losujemy ze zwracaniem kolejno dwa razy po jednej liczbie.

Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 15.

 Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z 30 kolejnych dni. Przyjmijmy, że liczbę L obsługiwanych klientów n-tego dnia opisuje funkcja L(n)=-n^2+34n+278, gdzie n jest liczbą naturalną spełniającą warunki n\geqslant 1 i n\leqslant 40.

Oceń prawdziwość poniższych zdań:

 Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów?

 Ile wówczas obsłużono klientów?