Podgląd testu : lo2@ma-3-2020-03-23-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10300 |
Podpunkt 1.1 (1 pkt)
Wartość wyrażenia a^8-b^8 jest podzielna przez:
Dane
a=19
b=17
b=17
Odpowiedzi:
| A. 887 | B. 650 |
| C. 710 | D. 566 |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10301 |
Podpunkt 2.1 (1 pkt)
(1 pkt) Reszta z dzielenia wielomianu
W(x)=x^{k+16}+x^{k+12}+x^{k+8}+x^{k+4}+x^k+x
przez dwumian P(x)=x^2-1 jest równa:
Dane
k=29
Odpowiedzi:
| A. 3x+1 | B. 6x |
| C. 6x+1 | D. 6x-1 |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10302 |
Podpunkt 3.1 (1 pkt)
(1 pkt) Wiadomo, że \log_{m}{n}=a. Wówczas wyrażenie
\log_{x}{y} jest równe:
Dane
m=3
n=5
x=15
y=9
n=5
x=15
y=9
Odpowiedzi:
| A. \frac{4}{a+1} | B. \frac{2}{a} |
| C. \frac{2}{a-1} | D. \frac{2}{a+1} |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10304 |
Podpunkt 4.1 (1 pkt)
Oblicz długość promienia okręgu o równaniu
x^2+y^2-6y-40=0.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20804 |
Podpunkt 5.1 (2 pkt)
« Ciąg liczbowy \left(a_n\right) określony jest następująco:
\begin{cases}
a_1=1 \\
a_{n+1}=a_n+0,15\text{, dla } n\in\mathbb{N_{+}}
\end{cases}
.
Oblicz sumę a_{k}+a_{k+1}+a_{k+2}+...+a_{l}.
Dane
k=45
l=65
l=65
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20805 |
Podpunkt 6.1 (2 pkt)
Ile liczb naturalnych sześciocyfrowych o niepowtarzających się cyfrach
i cyfrze setek większej od 2, można utworzyć z cyfr
0,1,2,3,4,5?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30794 |
Podpunkt 7.1 (1 pkt)
(2 pkt) W prostokącie ABCD dane są długości boków AB
i AD. Na boku CD zaznaczono punkt
E, zaś na odcinku EB punkt
M (zobacz rysunek).
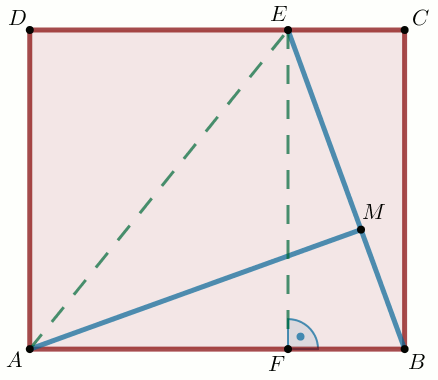

Wykorzystując podane poniżej długości odcinków oblicz pole powierzchni trójkąta ABM.
Dane
|AB|=39
|AD|=36
|DE|=24
|EM|=36
|AD|=36
|DE|=24
|EM|=36
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 7.2 (1 pkt)
(1 pkt) Oblicz długość odcinka AM.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 7.3 (2 pkt)
(1 pkt) Oblicz długość promienia okręgu opisanego na trójkącie
ABM.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30795 |
Podpunkt 8.1 (2 pkt)
Ciąg liczbowy \left(a_n\right) jest nieskończonym
ciągiem geometrycznym malejącym.
Suma trzech jego pierwszych wyrazów jest równa s, a iloczyn tych wyrazów
jest równy 1000.
Wyznacz iloraz tego ciągu.
Dane
s=62=62.00000000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.2 (1 pkt)
Wyznacz trzeci wyraz tego ciągu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.3 (1 pkt)
Oblicz sumę wszystkich wyrazów tego ciągu o numerach
nieparzystych.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20806 |
Podpunkt 9.1 (2 pkt)
(2 pkt) W półkole o promieniu długości R
wpisano trapez o obwodzie długości L,
którego wysokość jest liczbą niewymierną, a dłuższa podstawa trapezu
jest średnicą tego półkola.
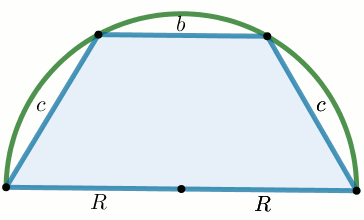

Wyznacz długość ramienia tego trapezu.
Dane
R=75
L=372
L=372
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.2 (2 pkt)
(2 pkt) Oblicz wysokość tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20808 |
Podpunkt 10.1 (2 pkt)
(2 pkt) « Ze wszystkich liczb naturalnych należących do zbioru
\{1,2,3,...,k\}
pięć razy losowano po jednej liczbie ze zwracaniem, otrzymując w ten sposób
pięciowyrazowy ciąg liczbowy
(a_1,a_2,a_3,a_4,a_5).
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymano ciąg, którego pierwszy wyraz jest podzielny przez m, a wyraz ostatni jest podzielny przez n.
Dane
k=30
m=5
n=6
m=5
n=6
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.2 (2 pkt)
(2 pkt) Ile byłoby równe to prawdopodobieństwo, gdyby losowanie odbywało się
bez zwracania?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. (5 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30797 |
Podpunkt 11.1 (1 pkt)
(2 pkt) Punkty A=(x_A, y_A),
B=(x_B, y_B) i C=(x_C, y_C)
są trzema kolejnymi wierzchołkami prostokąta ABCD
(kolejność wierzchołków jest zgodna z kierunkiem odwrotnym do ruchu wskazówek zegara).
Podaj odciętą wierzchołka D tego prostokąta.
Dane
x_A=-9
y_A=-6
x_B=-6
y_B=-3
x_C=-11
y_C=2
y_A=-6
x_B=-6
y_B=-3
x_C=-11
y_C=2
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (1 pkt)
(1 pkt) Podaj rzedną wierzchołka D tego prostokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.3 (1 pkt)
(1 pkt) Oblicz pole powierzchni tego prostokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.4 (1 pkt)
(1 pkt) Oblicz promień okręgu opisanego na tym prostokącie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.5 (1 pkt)
(1 pkt) Oblicz sinus kąta pod jakim przecinają się przekątne tego prostokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (5 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30798 |
Podpunkt 12.1 (2 pkt)
(2 pkt) Ostrosłup trójkątny ABCS o podstawie
ABC i wysokości H,
jest prawidłowy. Punkty E i F
są środkami jego krawędzi podstawy, odpowiednio AB i AC,
a kąt EFS jest prosty (zobacz rysunek).
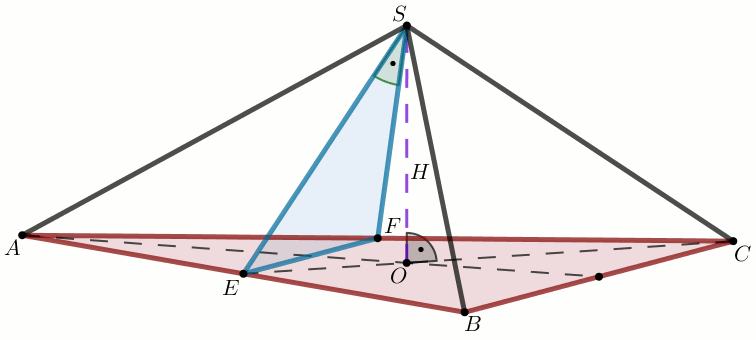

Wyraź długość krawędzi bocznej ostrosłupa za pomocą krawędzi podstawy a. Podaj \frac{|AS|}{a}.
Dane
H=10\sqrt{6}=24.49489742783178
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.2 (1 pkt)
(1 pkt) Oblicz długość krawędzi podstawy tego ostrosłupa.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.3 (1 pkt)
(1 pkt) Wyznacz cosinus kąta nachylenia płaszczyzny EFS do
płaszczyzny podstawy tego ostrosłupa.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.4 (1 pkt)
(1 pkt) Oblicz objętość ostrosłupa EBCFS.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 13. (7 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30799 |
Podpunkt 13.1 (1 pkt)
(1 pkt) Tworząca stożka ma długość l, a jego wysokość
długość h.
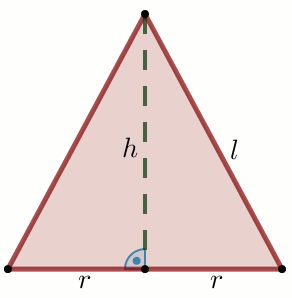
Wyznacz wzór funkcji f wyrażającej objętość
tego stożka w zależności od jego wysokości h.

Podaj wartość wyrażenia \frac{f(1)}{\pi}.
Dane
l=30
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.2 (1 pkt)
(1 pkt) Przedział (a,b) jest dziedziną tej funkcji.
Podaj liczbę b.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.3 (2 pkt)
(2 pkt) Oblicz \frac{f'(1)}{\pi}.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.4 (1 pkt)
(1 pkt) Wyznacz wysokość tego ze stożków, który ma największą
możliwą objętość.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.5 (2 pkt)
(2 pkt) Ile jest równą ta największa objętość stożka?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)