⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-02-zbio-licz-pp-4
| Zadanie 1. 1 pkt ⋅ Numer: pp-10043 ⋅ Poprawnie: 99/157 [63%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Dany jest zbiór
A=\left\lbrace n\in \mathbb{N}:\frac{7}{n}-3\in\mathbb{N} \right\rbrace
.
Wyznacz ilość elementów zbioru A.
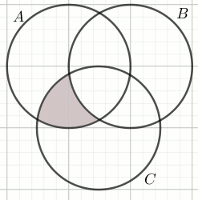
Odpowiedź:
\overline{\overline{A}}=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10221 ⋅ Poprawnie: 157/185 [84%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Odwrotnością liczby \frac{7}{2}\pi jest:
Odpowiedzi:
| A. -2\pi | B. -\frac{7}{2\pi} |
| C. \frac{2}{7\pi} | D. -\frac{2}{7\pi} |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10020 ⋅ Poprawnie: 262/356 [73%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Wyznacz ilość wszystkich rozwiązań równania
x(x-1)(x^2+9)=0.
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10168 ⋅ Poprawnie: 234/308 [75%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Równanie (2x-6)(x-2)=(6-2x)(x+2) ma dwa rozwiązania.
Są to liczby:
Odpowiedzi:
| A. 2\text{ i }3 | B. 3\text{ i }6 |
| C. 0\text{ i }3 | D. -3\text{ i }3 |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10147 ⋅ Poprawnie: 87/161 [54%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Licznik ułamka zwiększono o 53\%, a mianownik
tego ułamka zmniejszono o 15\%. Wówczas ułamek zwiększył
się o ........\%.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20121 ⋅ Poprawnie: 117/216 [54%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
« Liczba n jest dwucyfrowa i jest większa o
36 od sumy swoich cyfr. Jeżeli przestawimy
w liczbie n kolejność cyfr, to otrzymamy liczbę o
18 wiekszą od liczby n.
Oblicz n.
Odpowiedź:
n=
(wpisz liczbę całkowitą)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20060 ⋅ Poprawnie: 46/141 [32%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
«« W pewnej szkole przez trzy kolejne lata zmieniała się liczba uczniów.
W pierwszym roku liczba uczniów zmalała i na koniec roku była o
90\% mniejsza niż na początku. W drugim roku wzrosła
i ukończyło go 25\% więcej uczniów niż
pierwszy.
O ile procent, w stosunku do liczby uczniów kończących drugi rok,
zmieniła się (wzrosła lub zmalała) ich liczba w następnym roku, jeśli na
koniec trzeciego roku było tyle samo uczniów co na początku pierwszego?
Wynik zaokrąglij do 0,1% i wpisz go bez jednostki.
Odpowiedź:
ile\ procent=
(liczba zapisana dziesiętnie)