⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-04-funkcje-pp-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-10695 ⋅ Poprawnie: 367/948 [38%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Funkcja f każdej liczbie rzeczywistej
przypisuje połowę sześcianu tej liczby, pomniejszoną o 7.
Funkcję f opisuje wzór:
Odpowiedzi:
| T/N : f(x)=\frac{x^3-7}{2} | T/N : f(x)=0,5\frac{x^4}{x}-7 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10752 ⋅ Poprawnie: 357/577 [61%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Wykres funkcji y=\frac{21}{x} zawiera punkt o współrzędnych:
Odpowiedzi:
| A. \left(\sqrt{21},-\sqrt{21}\right) | B. \left(-\sqrt{3}, -7\sqrt{7}\right) |
| C. \left(-3,7\right) | D. \left(-3\sqrt{7}, -\sqrt{7}\right) |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10735 ⋅ Poprawnie: 277/402 [68%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Do wykresu funkcji określonej wzorem
f(x)=(m-2)x-7 należy punkt
S=(-2,-9).
Wyznacz wartość parametru m.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10691 ⋅ Poprawnie: 386/763 [50%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Wyznacz dziedzinę funkcji
f(x)=\frac{x+3}{\sqrt{6-x}}
i rozwiązanie zapisz w postaci sumy przedziałów. Liczba x_1
jest najmniejszm z końców liczbowych tych przedziałów, a liczba
x_2 jest największą liczbą całkowitą z dziedziny tej funkcji.
Podaj liczby x_1 i x_2.
Odpowiedzi:
| x_1 | = |
(wpisz liczbę całkowitą) |
| x_2 | = |
(wpisz liczbę całkowitą) |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10761 ⋅ Poprawnie: 127/237 [53%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Dana jest funkcja określona wzorem g(x)=-\frac{14-2x}{x}.
Połowę liczby g\left(\sqrt{2}\right) zapisz
w postaci \frac{m+n\sqrt{k}}{p},
gdzie m,n,k,p\in\mathbb{Z}.
Odpowiedź:
| \frac{m+n\sqrt{k}}{p}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 6. 1 pkt ⋅ Numer: pp-10743 ⋅ Poprawnie: 58/100 [58%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« Dziedziną funkcji g(x)=\frac{2x-12}{|6-x|}
jest zbiór (6,+\infty).
Zatem:
Odpowiedzi:
| A. ZW_{g}=\{-2,2\} | B. ZW_{g}=\mathbb{R}-\{-2\} |
| C. ZW_{g}=\mathbb{R}-\{2\} | D. ZW_{g}=\{2\} |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10762 ⋅ Poprawnie: 251/300 [83%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Podaj największą wartość funkcji f, której wykres pokazano na rysunku:
Odpowiedź:
f_{max}(x)=
(wpisz liczbę całkowitą)
| Zadanie 8. 1 pkt ⋅ Numer: pp-11689 ⋅ Poprawnie: 46/68 [67%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Wyznacz największą wartość funkcji określonej wzorem f(x)=\frac{5}{2}x-\frac{3}{2}
w przedziale \langle -3,5\rangle.
Odpowiedź:
| f_{max}(x)= | |
| Zadanie 9. 1 pkt ⋅ Numer: pp-10751 ⋅ Poprawnie: 205/370 [55%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Wyznacz miejsce zerowe funkcji
f(x)=\sqrt{20}(x-2)-7.
Odpowiedź:
| Wpisz odpowiedź: |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 10. 1 pkt ⋅ Numer: pp-10700 ⋅ Poprawnie: 508/905 [56%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji h:
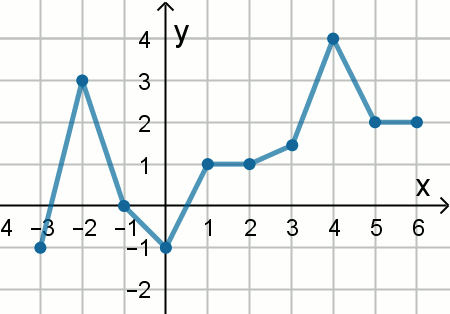
Jaką długość ma najdłuższy przedział, w którym funkcja h jest monotoniczna?
Odpowiedź:
d=
(wpisz liczbę całkowitą)