⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-04-funkcje-pp-3
| Zadanie 1. 1 pkt ⋅ Numer: pp-10695 ⋅ Poprawnie: 368/949 [38%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Funkcja f każdej liczbie rzeczywistej
przypisuje połowę sześcianu tej liczby, pomniejszoną o 9.
Funkcję f opisuje wzór:
Odpowiedzi:
| T/N : f(x)=0,5\frac{x^4}{x}-9 | T/N : f(x)=\frac{1}{2}\left(x^3-18\right) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10754 ⋅ Poprawnie: 262/431 [60%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Punkt M o rzędnej równej 14
należy do wykresu funkcji f(x)=2+\frac{4}{1-x}.
Wyznacz odciętą punktu M.
Odpowiedź:
| x_M= | |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10735 ⋅ Poprawnie: 277/402 [68%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Do wykresu funkcji określonej wzorem
f(x)=(m+1)x+4 należy punkt
S=(3,19).
Wyznacz wartość parametru m.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10731 ⋅ Poprawnie: 403/922 [43%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Na rysunku przedstawiono wykres funkcji
y=f(x).
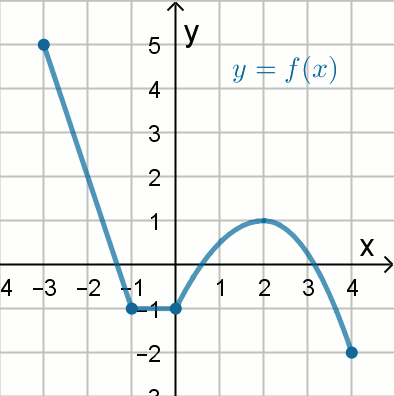
W którym z przedziałów, funkcja przyjmuje wartość 1:
Odpowiedzi:
| A. (-3,-2) | B. (-1,2) |
| C. (0;1,(9)\rangle | D. (2,3) |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10682 ⋅ Poprawnie: 675/828 [81%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Dziedziną funkcji f określonej wzorem
f(x)=\frac{x-4}{x^2-7x} może być zbiór:
Odpowiedzi:
| A. \mathbb{R}-\{-7,7\} | B. \mathbb{R}-\{-7,0\} |
| C. \mathbb{R}-\{0,7\} | D. \mathbb{R} |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10692 ⋅ Poprawnie: 127/169 [75%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Dziedziną funkcji f określonej wzorem
f(x)=\log{(x^2+49)}
jest zbiór:
Odpowiedzi:
| A. (-7;7) | B. \mathbb{R} |
| C. (-\infty;-7)\cup(7;+\infty) | D. \mathbb{R}-\{-7;7\} |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10681 ⋅ Poprawnie: 639/895 [71%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Wyznacz dziedzinę D_f funkcji określonej wzorem
f(x)=\sqrt{-x-10}
.
Podaj największą liczbę całkowitą, która należy do zbioru D_f.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 8. 1 pkt ⋅ Numer: pp-10684 ⋅ Poprawnie: 164/246 [66%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Dla którego z podanych zbiorów liczb naturalnych wyrażenie
\frac{\sqrt{x-7}}{x-9}
ma sens liczbowy:
Odpowiedzi:
| A. \{0,7,12\} | B. \{8,9,13\} |
| C. \{6,7,10\} | D. \{7,10\} |
| Zadanie 9. 1 pkt ⋅ Numer: pp-10758 ⋅ Poprawnie: 180/291 [61%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
« Dla argumentu x=\frac{1}{\sqrt{6}-1} oblicz wartość
funkcji określonej wzorem f(x)=-2x+4 i zapisz wynik
w najprostszej postaci \frac{m+n\sqrt{k}}{p}, gdzie
m,n,k,p\in\mathbb{Z}.
Podaj liczby m, n, k i p.
Odpowiedź:
| \frac{m+n\sqrt{k}}{p}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 10. 1 pkt ⋅ Numer: pp-10761 ⋅ Poprawnie: 128/238 [53%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
« Dana jest funkcja określona wzorem g(x)=-\frac{16-2x}{x}.
Połowę liczby g\left(\sqrt{2}\right) zapisz
w postaci \frac{m+n\sqrt{k}}{p},
gdzie m,n,k,p\in\mathbb{Z}.
Odpowiedź:
| \frac{m+n\sqrt{k}}{p}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 11. 1 pkt ⋅ Numer: pp-10719 ⋅ Poprawnie: 122/163 [74%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
« Funkcja f przyporządkowuje każdej liczbie naturalnej
większej od 1 resztę z dzielenia tej liczby przez 23.
Spośród liczb: f(80), f(89), f(100), f(106) największą jest:
Odpowiedzi:
| A. f(89) | B. f(106) |
| C. f(80) | D. f(100) |
| Zadanie 12. 1 pkt ⋅ Numer: pp-10717 ⋅ Poprawnie: 187/246 [76%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Funkcja f przyporządkowuje każdej liczbie
naturalnej resztę z dzielenia tej liczby przez 7.
Oblicz wartość wyrażenia \frac{f(26)}{f(30)}.
Odpowiedź:
| \frac{f(m)}{f(n)}= | |
| Zadanie 13. 1 pkt ⋅ Numer: pp-10748 ⋅ Poprawnie: 107/128 [83%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
Funkcja f opisana jest wzorem:
f(x)=\sqrt[3]{3+4x}.
Wówczas f(x-3) jest równa:
Odpowiedzi:
| A. \sqrt[3]{3+4x}-3 | B. \sqrt[3]{4x-1} |
| C. \sqrt[3]{4x-9} | D. \sqrt[3]{-4x} |
| Zadanie 14. 1 pkt ⋅ Numer: pp-10740 ⋅ Poprawnie: 100/128 [78%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
Funkcja f opisana jest wzorem
f(x)=\frac{1+12x}{x-1} dla pewnego argumentu
przyjmuje wartość \sqrt{145}.
Argumentem tym jest:
Odpowiedzi:
| A. 145+\sqrt{145} | B. \frac{\sqrt{145}+1}{\sqrt{145}-12} |
| C. \left(\sqrt{145}+1\right)^2 | D. \sqrt{145}-1 |
| Zadanie 15. 1 pkt ⋅ Numer: pp-10711 ⋅ Poprawnie: 215/282 [76%] | Rozwiąż |
Podpunkt 15.1 (1 pkt)
Funkcja f określona jest wzorem
f(x)=2\sqrt{x} dla x\in\{1,4,9,16,25,36,49\}.
Do zbioru wartości tej funkcji nie należy liczba:
Odpowiedzi:
| A. 4 | B. 14 |
| C. 12 | D. 3 |
| E. 10 | F. 8 |
| Zadanie 16. 1 pkt ⋅ Numer: pp-11689 ⋅ Poprawnie: 46/68 [67%] | Rozwiąż |
Podpunkt 16.1 (1 pkt)
Wyznacz największą wartość funkcji określonej wzorem f(x)=4x+1
w przedziale \langle -4,6\rangle.
Odpowiedź:
| f_{max}(x)= | |
| Zadanie 17. 1 pkt ⋅ Numer: pp-10746 ⋅ Poprawnie: 170/369 [46%] | Rozwiąż |
Podpunkt 17.1 (1 pkt)
« Funkcja f opisana jest wzorem
f(x)=|x|-11, dla
x\in\mathbb{C}.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : wykres tej funkcji nie ma punktów wspólnych z osią Oy | T/N : wartości tej funkcji są liczbami naturalnymi |
| T/N : dla pewnego argumentu funkcja ta przyjmuje wartość -5 |
| Zadanie 18. 1 pkt ⋅ Numer: pp-10706 ⋅ Poprawnie: 751/959 [78%] | Rozwiąż |
Podpunkt 18.1 (1 pkt)
Liczba 1 jest miejscem zerowym
funkcji f(x)=(2m-1)x-1.
Wyznacz wartość parametru m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 19. 1 pkt ⋅ Numer: pp-10700 ⋅ Poprawnie: 508/905 [56%] | Rozwiąż |
Podpunkt 19.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji h:
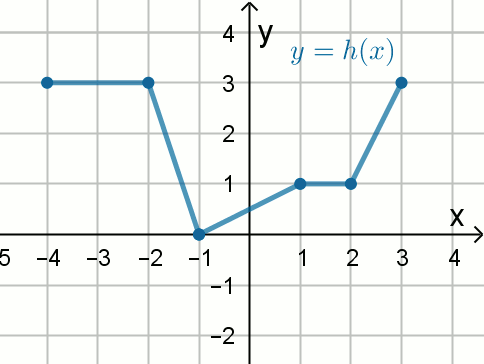
Jaką długość ma najdłuższy przedział, w którym funkcja h jest monotoniczna?
Odpowiedź:
d=
(wpisz liczbę całkowitą)