Podgląd testu : lo2@sp-04-funkcje-pr-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-10739 ⋅ Poprawnie: 323/426 [75%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Punkt B=(-8,y) należy do wykresu funkcji
f(x)=\frac{-3-x^2}{x-1}.
Wyznacz y.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10683 ⋅ Poprawnie: 999/1113 [89%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Dziedziną funkcji f jest przedział:
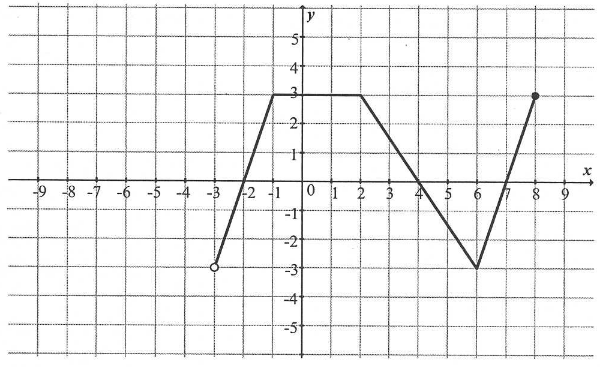

Odpowiedzi:
| A. (-3, 8\rangle | B. \langle -3, 3\rangle |
| C. \langle 0, 3\rangle | D. (0, 8\rangle |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10705 ⋅ Poprawnie: 499/587 [85%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji y=f(x).
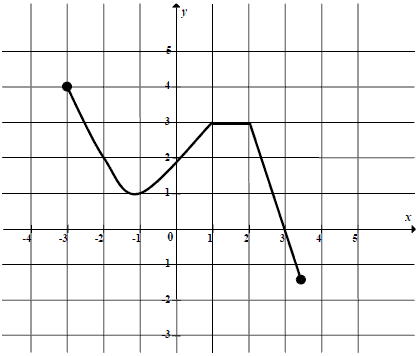

Wyznacz największą wartość funkcji f w przedziale \langle -2, 1\rangle.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pr-10089 ⋅ Poprawnie: 6/6 [100%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
» Dana jest funkcja f określona wzorem
f(x)=\left\lbrace
\begin{array}{ll}
(x+4)^3 & \text{dla } -4\leqslant x \lessdot -2\\
-x^2-8x-12 & \text{dla } -2\leqslant x \leqslant 2
\end{array}
.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : f(-5)+f(-4) > 0 | T/N : f(-1)-f(-6) \lessdot 0 |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11691 ⋅ Poprawnie: 37/56 [66%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Wyznacz najmniejszą wartość funkcji określonej wzorem f(x)=-\frac{1}{3}x^2+2,
w przedziale \langle 2,4\rangle.
Odpowiedź:
| f_{min}(x)= | |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10726 ⋅ Poprawnie: 326/865 [37%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Rysunek przedstawia wykres funkcji f:
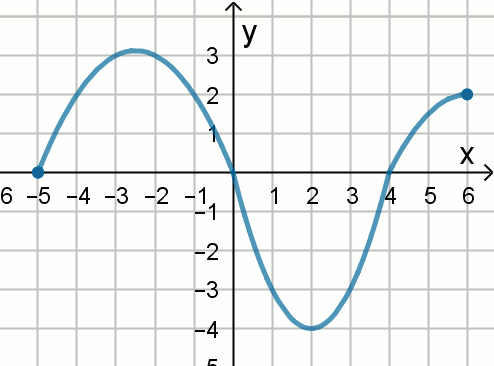

Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : dziedziną funkcji jest przedział (-5,6) | T/N : f(x) \lessdot 0 dla x > 0 |
| Zadanie 7. 1 pkt ⋅ Numer: pr-10093 ⋅ Poprawnie: 2/3 [66%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
» Funkcja f opisana jest wzorem
f(x)=\left\lbrace
\begin{array}{ll}
x^3-1 & \text{dla }x \in(-1,0\rangle\\
x^5-28 & \text{dla }x > 2\\
2x^3-5x^2 & \text{dla }x\in(0,2)
\end{array}
i ma k miejsc zerowych.
Wyznacz liczbę k.
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 8. 1 pkt ⋅ Numer: pp-10698 ⋅ Poprawnie: 205/563 [36%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
«« Dziedziną funkcji f jest przedział
\langle -5,4\rangle:
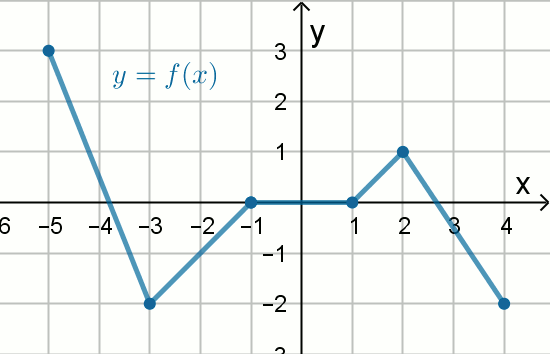
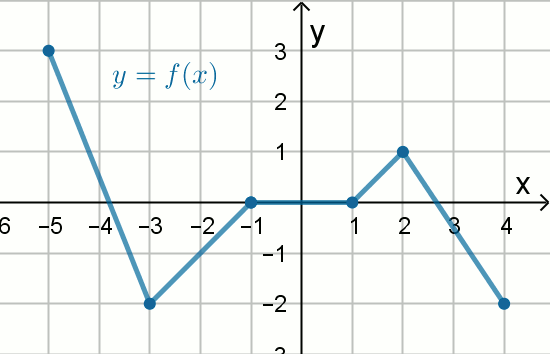
Jaką długość ma najdłuższy przedział, w którym funkcja f jest malejąca?
Odpowiedź:
d=
(wpisz liczbę całkowitą)
| Zadanie 9. 1 pkt ⋅ Numer: pr-10279 ⋅ Poprawnie: 3/4 [75%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Które z wzorów opisują funkcję parzystą?
Odpowiedzi:
| T/N : f(x)=\frac{x^2+3x}{x^2+4} | T/N : f(x)=\frac{x-5}{2x^2} |
| T/N : f(x)=\frac{|x|}{x} |